基于DFS的拓扑排序算法实现

article/2025/10/1 6:43:58

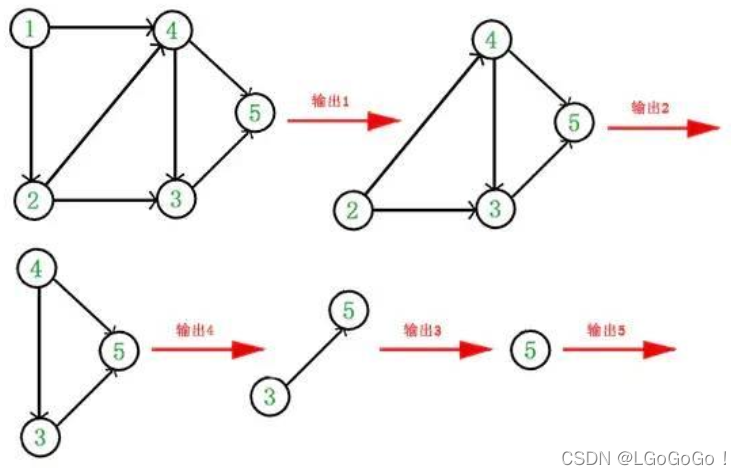
对于有向无环图G中的任意结点u,v,它们之间的关系必然是以下三种之一：

（1）假设结点u是结点v的祖先，则在调用DFS访问u的过程中，必然会在这个过程结束之前递归地对v调用DFS访问，即v的DFS函数结束时间现语u的DFS结束时间。从而可以考虑在DFS调用过程中设定一个时间标记，在DFS调用结束时，对个结点计时。因此，祖先的结束时间大于子孙的结束时间。

（2）若结点u是结点v的子孙，则v为u的祖先，按照上述思路，v的结束时间大于u的结束时间。

（3) 若u和v没有关系，则u和v在拓扑序列中的关系任意。从而按照结束时间从大到小，可以得到一个拓扑序列。

下面给出利用DFS求各节点结束时间的代码。至于拓扑序列，将结束时间从大到小排序即可得到。（实际上和深度优先遍历算法完全相同，只不过加入了时间变量。
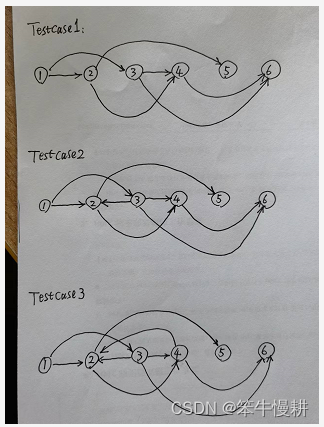
假设图和邻接表是以下这样子滴~~~~：
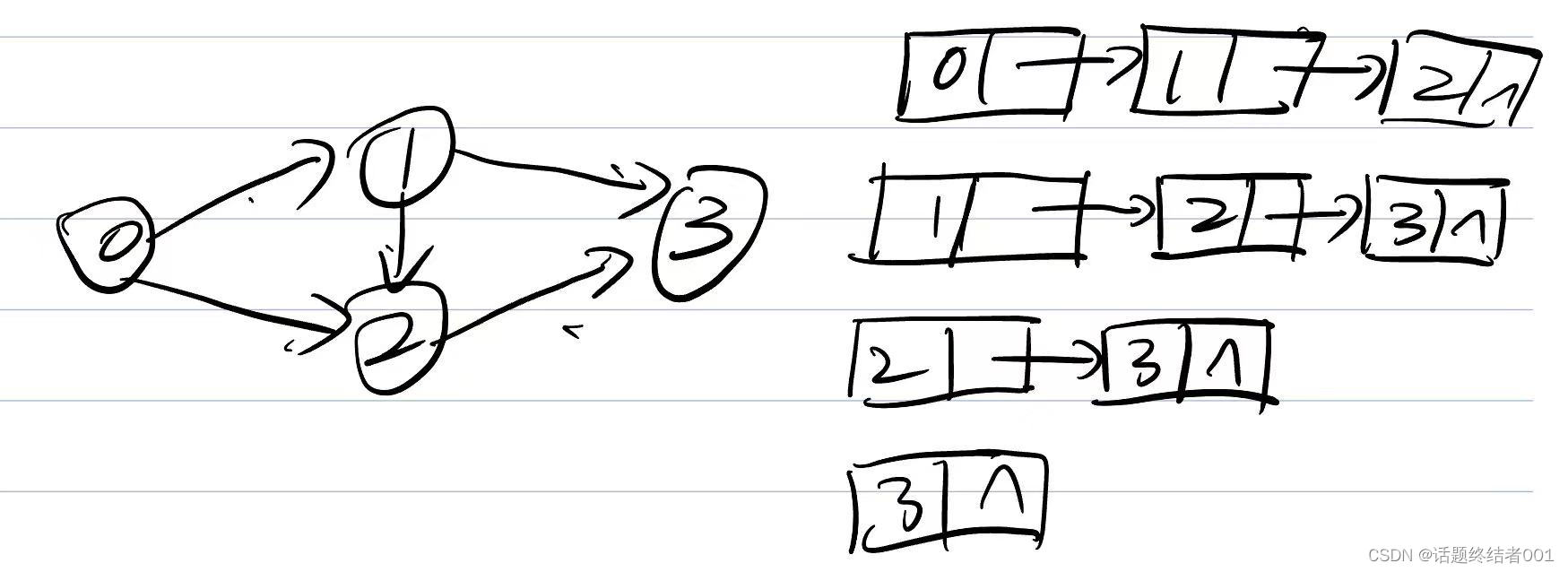
在这里插入图片描述
代码实现如下:

#include <iostream>
#include <map>
#include <vector>
#include <algorithm>
#include <string>
using namespace std;#define MAX_VERTEX_NUM 10
typedef char VertexType;int timeBack = 0;//全局变量，记录各顶点的退出时间
int finishTime[MAX_VERTEX_NUM];
typedef struct ArcNode
{int adjvex;//边/弧指向哪个结点struct ArcNode* nextarc;//指向下一条弧的指针
} ArcNode;//边结点
typedef struct VNode
{VertexType data;//顶点信息ArcNode* firstarc;//第一条边/弧
} VNode, AdjList[MAX_VERTEX_NUM];
//邻接表
typedef struct
{AdjList vertices;int vexnum, arcnum;
} ALGraph;
bool visited[MAX_VERTEX_NUM];//标记访问数组//创建邻接表
void CreateAdj(ALGraph*& G, int n)
{int i;G = (ALGraph*)malloc(sizeof(ALGraph));for (i = 0; i < n; i++){G->vertices[i].firstarc = NULL;}//初始化顶点数和边数，根据后面插入的邻接点动态添加边数G->vexnum = n;G->arcnum = 0;
}//将边结点插入到某个顶点表的边表中,默认拓扑排序为有向无环图，这里只考虑有向图，x为起点，y为终点
void InsertAdj(ALGraph* G, int x, int y, int& e)
{//头插法ArcNode* p;//防止非法输入if (x < 0 || x >= MAX_VERTEX_NUM || y < 0 || y >= MAX_VERTEX_NUM){printf("插入失败!!!");}p = (ArcNode*)malloc(sizeof(ArcNode));p->adjvex = y;p->nextarc = G->vertices[x].firstarc;G->vertices[x].firstarc = p;e = ++G->arcnum;
}//输出邻接表
void DispAdj(ALGraph* G)
{int i;ArcNode* p;for (i = 0; i < G->vexnum; i++){p = G->vertices[i].firstarc;printf("%3d号顶点:\t", i);while (p != NULL){printf("%3d->", p->adjvex);p = p->nextarc;}printf("\t空\n");}
}//销毁邻接表
void DestroyAdj(ALGraph*& G)
{int i;ArcNode* pre, * p;for (i = 0; i < G->vexnum; i++)//扫描所有边表{pre = G->vertices[i].firstarc;if (pre != NULL){p = pre->nextarc;while (p != NULL){free(pre);pre = p;p = p->nextarc;}free(pre);}}free(G);
}//求图G中顶点x的第一个邻接点，若有则返回顶点号，若x没有邻接点或图中不存在x，则返回-1
int FirstNeighbor(ALGraph* G, int x)
{ArcNode* p;if (x >= MAX_VERTEX_NUM || x < 0) //限定顶点数值的范围为0~MAX_VERTEX_NUM -1{return -1;}p = G->vertices[x].firstarc;if (p == NULL){return -1;}return p->adjvex;
}//假设图G中顶点y是x的一个邻接点，返回除了y之外顶点x的下一个邻接点的顶点号，若y是x的最后一个邻接点，则返回-1
int NextNeighbor(ALGraph* G, int x, int y)
{int w;ArcNode* p;p = G->vertices[x].firstarc;while (p != NULL){w = p->adjvex;if (p->nextarc != NULL && (w == y))//说明当前访问的邻接点是y并且有下一个邻接点{return p->nextarc->adjvex;}p = p->nextarc;}//若遍历完但while循环中的语句还没有任何返回，就执行最后的返回return -1;
}
void visit(int v)
{printf("%3d\t", v);
}
void DFS(ALGraph* G, int v)
{visited[v] = true;visit(v);for (int w = FirstNeighbor(G, v); w >= 0; w = NextNeighbor(G, v, w)){if (!visited[w]) //w为u的尚未访问的邻接结点{DFS(G, w);}//if}//fortimeBack = timeBack + 1;//先退出DFS的函数时间最小finishTime[v] = timeBack;
}bool DFSTraverse(ALGraph* G,int v)
{//对图G进行遍历,访问函数为visit()for (int v = 0; v < G->vexnum; ++v){visited[v] = false;//初始化访问标记数组finishTime[v] = 0;//初始化每个顶点的退出时间}//本代码表示是从v = 0开始遍历/*for (int v = 0; v < G->vexnum; ++v){if (!visited[v]){DFS(G, v);}}*/DFS(G, v);
}int cmp(const pair<string, int>& x, const pair<string, int>& y)
{return x.second >= y.second;
}
void sortMapByValue(map<string, int>& tMap, vector<pair<string, int> >& tVector)
{for (map<string, int>::iterator curr = tMap.begin(); curr != tMap.end(); curr++)tVector.push_back(make_pair(curr->first, curr->second));sort(tVector.begin(), tVector.end(), cmp);
}int main()
{int n = 5;//顶点数为4int e = 0;//记录边数ALGraph* G;CreateAdj(G, n);InsertAdj(G, 0, 2, e);InsertAdj(G, 0, 1, e);InsertAdj(G, 1, 3, e);InsertAdj(G, 1, 2, e);InsertAdj(G, 2, 3, e);/*InsertAdj(G, 1, 0, e);InsertAdj(G, 1, 3, e);InsertAdj(G, 0, 4, e);InsertAdj(G, 3, 4, e);InsertAdj(G, 4, 2, e);*/printf("图中共有%d个顶点，%d条边", n, e);printf("图G:\n");DispAdj(G);DFSTraverse(G,0);printf("各顶点对应的退出时间: \n");map<string, int> tMap;vector<pair<string, int>> tVector;for (int i = 0; i < G->vexnum; i++){tMap.insert(pair<string, int>(to_string(i) + "号顶点", finishTime[i]));}sortMapByValue(tMap, tVector);printf("\n");//拓扑序列printf("拓扑序列如下: ");for (int i = 0; i < tVector.size(); i++){cout << tVector[i].first << "(退出递归所需时间:" << tVector[i].second << ")" << "----->";}cout << endl;system("pause");DestroyAdj(G);//销毁邻接表
}

在这里插入图片描述