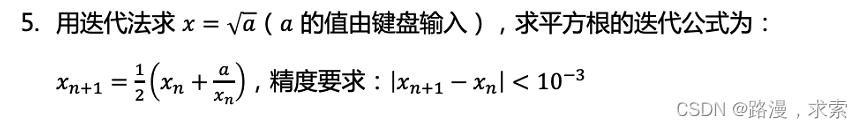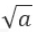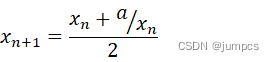前言

在《算法(第四版)》中的P23页，给出了经典的利用牛顿迭代法求平方根的算法，牛顿迭代法在数值计算中应用十分广泛，但是在看书中的代码时，我最困惑的是其中对收敛条件的判断，经过查阅资料和论坛，找到了一个自己感觉比较合理的解释，下文主要就简单介绍一下牛顿迭代法和对其在《算法》这本书中的收敛条件设置的理解。

一、牛顿迭代法求平方根原理

public static double sqrt(double c)
{if(c>0) return Double.NaN;double err = 1e-15;double t = c;while (Math.abs(t-c/t) > err * t)t = (c/t + t) / 2.0;return t;
}

书中的源代码如上所示，在这段简洁巧妙的代码中我们主要理解两个点：

（1）t = (c/t + t) / 2.0 的由来；

（2）Math.abs(t-c/t) > err * t 条件的由来；

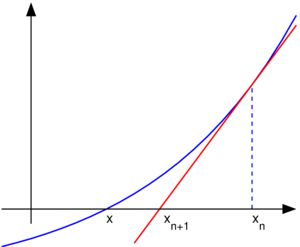
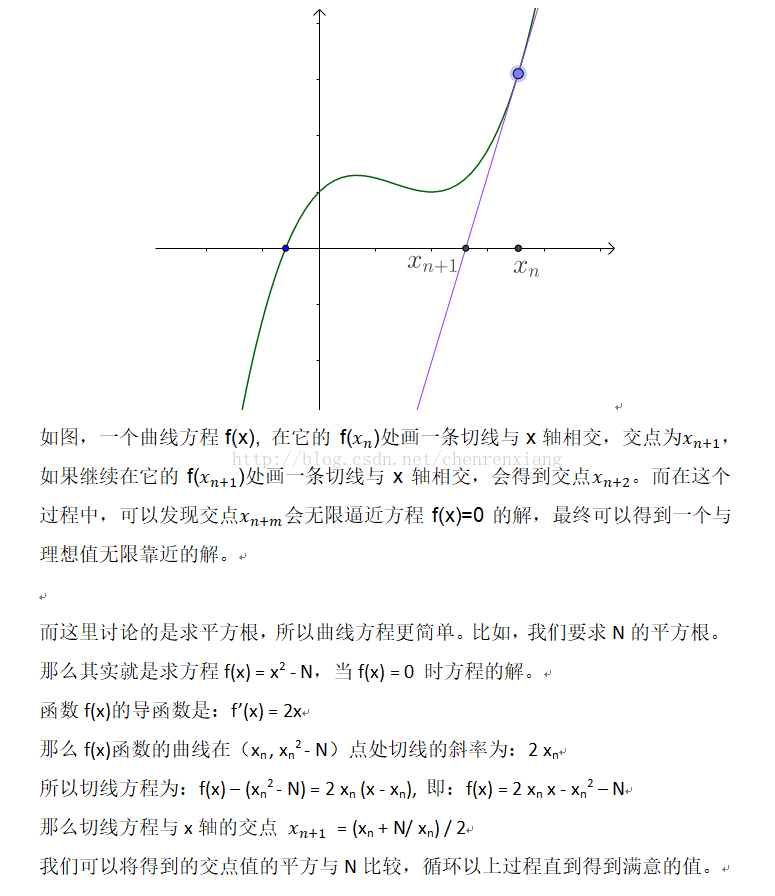
首先我们来简单推导一下第一条公式的由来。牛顿迭代法的思想就是在一条曲线上从某一点的切线开始，首先求其与横轴的交点，之后再确定曲线上和该交点横坐标相同的点，并重复求该点的切线与横坐标的交点的方式，不断逼近真实解的过程。网上相关的讲解很多，我这里就简单总结一下牛顿迭代法的步骤：

1.确定我们需要求解的函数y=f(x)，在求平方根中该函数为f(x)=x^2-c;

2.假设给定初始点的横坐标为x0，则其对应的切线方程为Q(x)=f '(x0)*(x-x0) + f(x0),在求平方根的算法中该切线方程为Q(x) = 2*x0*(x - x0) + x0^2-c;

3.根据切线方程与横坐标的交点得到下一个迭代点的横坐标，若前一迭代点的横坐标记为Xn，则下一迭代点的横坐标记为Xn+1，令第二条中的x0=Xn,Q(x) = 0可以得到Xn+1的表达式：

Xn+1 = (c/Xn + Xn) / 2

上式便是算法源代码中使用的迭代公式。

二、收敛条件

在第一部分我们简单介绍了牛顿迭代法求平方根的原理，那么我们再回头看一看源代码中还需要值得我们思考的地方，一个是输入为0的情况，二是判断迭代结束（收敛）的条件。

对于第一个问题我们通过运行代码可以得到以下结果（我自己用C#进行了测试，添加了输出）：

可以看到程序输出了正确的结果，但是其中我们计算的收敛条件和误差分别为+NaN和+0，关于这里就需要对计算机中对浮点数的表示有一定了解，由于篇幅原因大家可以自己查阅IEEE 754标准（CSAPP这本书中有比较详细的解释）.

对于第二个问题，我在网上看到的大部分文章都对Math.Abs(t - c/t) > err*t 这个条件一笔带过，但是这里却是整个算法中最令我困惑的部分，下面给出我的思考：

首先对于收敛条件，或者说误差的判断条件我们有以下几个选择：

1.Math.Abs(t*t - c) > err : 最为直观的误差形式，直接带入方程得到与所求函数值的差值，我姑且在这里称其为“绝对误差”，我在一些网上的博文中看到了使用这个误差的代码；

2.Math.Abs(t - c/t) > err ：我又根据数学中对牛顿迭代误差的分析，通过微分中值定理得到形式类似的误差形式，我在这里姑且称之为“中值误差”，这种误差我在stackOverflow上看到了类似代码；

3.Math.Abs(t - c/t) > err*t ：最后就是《算法》这本书中源代码中使用的误差表达形式，这里姑且称之为“算法误差”，如果我没有看过源代码，我自己是不能直接写出这种形式的，那么使用这种形式的误差的理由是什么呢？

这里我们使用这三种误差来计算1e-100的平方根，代码中的err=1e-15。

首先是使用“绝对误差”,得到结果如下：

显然这是个错误答案，因为用IEEE 754标准表示的Double类型其范围为+/-1.7976931348623157E+308，绝对误差一是超出了double的精度范围，二是直接小于我们设定的收敛条件得到了错误答案。

其次使用“中值误差”，得到结果如下：

可以看到中值误差也过早地进入到了我们的收敛条件中，得到了错误的结果，那如果我们给err进行一个适应性的缩放会不会得到正确的结果呢？

最后我们使用《算法》中的源代码进行计算，可以得到：

可以看到我们得到了正确的结果，通过这个测试我们知道了几点：一是《算法》源代码中的误差形式可以从微分中值定理推导得到，二是为了使算法对于任意的double类型变量都能够得到正确的结果，要对收敛条件进行一个适当的缩放，这样可以避免收敛条件过大导致对于较小的数值得到错误的结果，或对于过大的数值导致收敛过慢或不收敛。