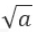数据结构——图——拓扑排序算法

article/2025/10/1 7:27:36

数据结构——图——拓扑排序算法

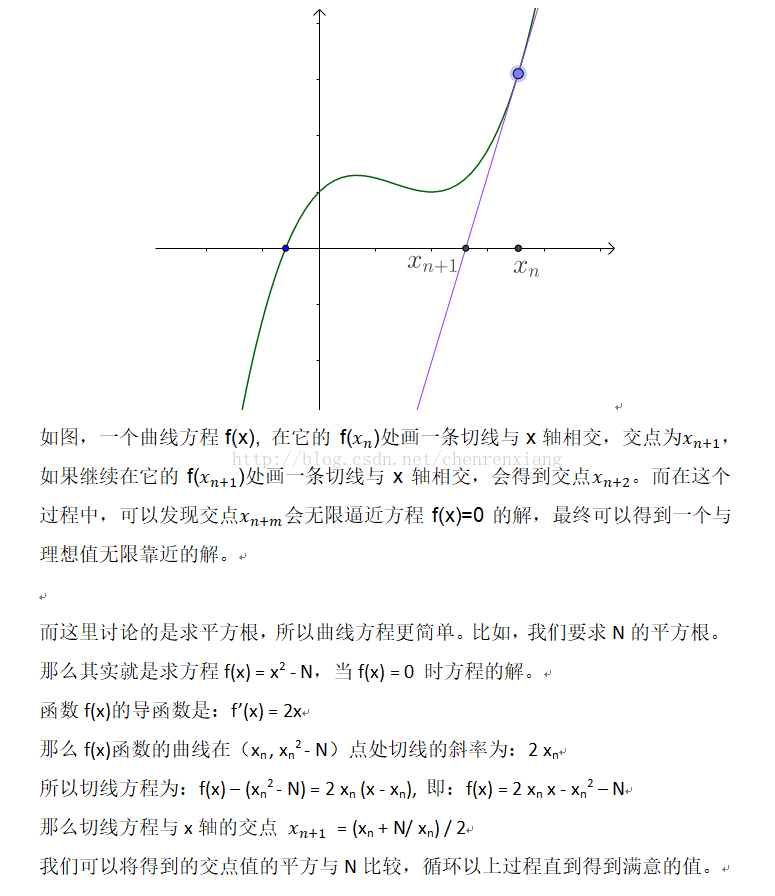
对AOV网进行拓扑排序的基本思路是:从AOV网中选择一个入度为0的顶点输出，然后删去此顶点，并删除以此顶点为尾的弧，继续重复此步骤，直到输出全部顶点或者AOV 网中不存在入度为0的顶点为止。

首先我们需要确定一下这个图需要使用的数据结构。前面求最小生成树和最短路径时，我们用的都是邻接矩阵，但由于拓扑排序的过程中，需要删除顶点，显然用邻接表会更加方便。因此我们需要为AOV网建立一个邻接表。考虑到算法过程中始终要查找入度为0的顶点，我们在原来顶点表结点结构中，增加一个入度域in，结构如表7-8-1所示,其中in就是入度的数字。

在这里插入图片描述
因此对于图7-8-2的第一幅图AOV网，我们可以得到如第二幅图的邻接表数据结构。

在这里插入图片描述

在拓扑排序算法中，涉及的结构代码如下。

typedef struct EdgeNode    /*边表结点*/
{int adjvex;            /*邻接点域，存储该顶点对应的下标*/int weight;            /*用于存储权值，对于非网图可以不需要*/struct EdgeNode* next; /*链域，指向下一个邻接点*/}EdgeNode;typedef struct VertexNode   /*顶点表结点*/
{int in;                 /*顶点入度*/int data;               /*顶点域，存储顶点信息*/EdgeNode* firstedge;     /*边表头指针*/
} VertexNode,AdjList[MAXVEX];typedef struct
{AdjList adjList;int numVertexes, numEdges;    /*图中当前顶点数和边数*/
}graphAdjList,*GraphAdjList;

在管法由．我还需要辅助的数据结构–栈，用来存储处理过程中入度为0的顶点，目的是为了避免每个查找时都要去遍历顶点表找有没有入度为0的顶点。

现在我们来看代码,并且模拟运行它。


/*拓扑排序，若GL无回路，则输出拓扑排序序列并返回true，若有回路返回false*/
bool TopologicalSort(GraphAdjList GL)
{EdgeNode* e;int i, k, gettop;int top = 0;        /*用于栈指针下标*/int count = 0;      /*用于统计输出顶点的个数*/int* stack;         /*建栈存储入度为0的顶点*/stack = (int*)malloc(GL->numVertexes * sizeof(int));for (i=0;i<GL->numVertexes;i++){if (GL->adjList[i].in==0){stack[++top] = i;   /*将入度为0的顶点入栈*/}}while (top!=0){gettop = stack[top--];/*出栈*/printf("%d ->",GL->adjList[gettop].data);/*打印此顶点*/count++;/*统计输出顶点数*/for (e=GL->adjList[gettop].firstedge;e;e=e->next){/*对此顶点弧表遍历*/k = e->adjvex;if (!(--GL->adjList[k].in))/*将k号顶点邻接点的入度减1*/{stack[++top] = k;/*若为0则入栈，以便于下次循环输出*/}}}if (count<GL->numVertexes)/*如果count小于顶点数，说明存在环*/{return false;}else{return true;}
}

在这里插入图片描述

1．程序开始运行，第3~7行都是变量的定义，其中stack是一个栈，用来存储整型的数字。
2．第8~10行，作了一个循环判断，把入度为0的顶点下标都入栈，从图7-8-3的右图邻接表可知，此时 stack应该为:{0，1，3}，即v0、v1、v3的顶点入度为0，如图7-8-3所示。

在这里插入图片描述
3．第12~23行，while循环，当栈中有数据元素时，始终循环。
4．第14~～16行，v3出栈得到gettop=3。并打印此顶点，然后count 加1。
5．第17~22行，循环其实是对v3顶点对应的弧链表进行遍历，即图7-8-4中的灰色部分，找到v3连接的两个顶点v2和 v13，并将它们的入度减少一位，此时v2和v3的in值都为1。它的目的是为了将v3顶点上的弧删除。
在这里插入图片描述
6．再次循环，第12~23行。此时处理的是顶点v1。经过出栈、打印、count=2
后，我们对v1到v2、V4、v8的弧进行了遍历。并同样减少了它们的入度数，此时v2入度为0，于是由第20~21行知，v2入栈，如图7-8-5所示。试想，如果没有在顶点表中加入 in这个入度数据域，20行的判断就必须要是循环，这显然是要消耗时间的,我们利用空间换取了时间。
在这里插入图片描述
7．接下来，就是同样的处理方式了。图7-8-6展示了V2 V6 V0 V4 V5 V8的打印删除过程，后面还剩几个顶点都类似,就不图示了。