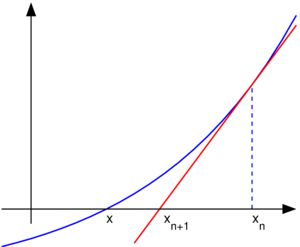
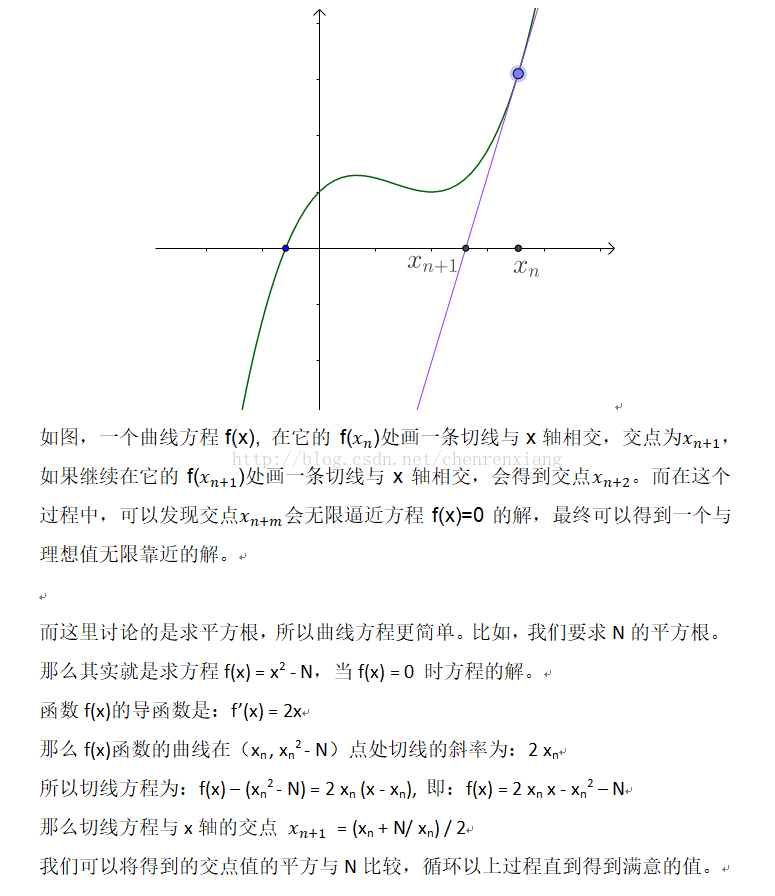
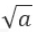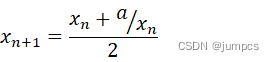求n的平方根,先假设一猜测值X0 = 1,然后根据以下公式求出X1,再将X1代入公式右边,继续求出X2…通过有效次迭代后即可求出n的平方根,Xk+1
![]()
先让我们来验证下这个巧妙的方法准确性,来算下2的平方根 (Computed by Mathomatic)
1-> x_new = ( x_old + y/x_old )/2
y
(x_old + -----)
x_old
#1: x_new = ---------------
2
1-> calculate x_old 1
Enter y: 2
Enter initial x_old: 1
x_new = 1.5
1-> calculate x_old 2
Enter y: 2
Enter initial x_old: 1
x_new = 1.4166666666667
1-> calculate x_old 3
Enter y: 2
Enter initial x_old: 1
x_new = 1.4142156862745
1-> calculate x_old 10
Enter y: 2
Enter initial x_old: 1
Convergence reached after 6 iterations.
x_new = 1.4142135623731
...
可见,随着迭代次数的增加,运算值会愈发接近真实值。很神奇的算法,可是怎么来的呢? 查了下wikipedia和wolfram,原来算法的名字叫Newton’s Iteration (牛顿迭代法)。
下面是极其つまらない(boring)的数理介绍,不喜欢数学的言下之意也就是绝大部分人可以略过了。
简单推导

假设f(x)是关于X的函数:
求出f(x)的一阶导,即斜率:
![]()
简化等式得到:
![]()
然后利用得到的最终式进行迭代运算直至求到一个比较精确的满意值,为什么可以用迭代法呢?理由是中值定理(Intermediate Value Theorem):
如果f函数在闭区间[a,b]内连续,必存在一点x使得f(x) = c,c是函数f在闭区间[a,b]内的一点
我们先猜测一X初始值,例如1,当然地球人都知道除了1本身之外任何数的平方根都不会是1。然后代入初始值,通过迭代运算不断推进,逐步靠近精确值,直到得到我们主观认为比较满意的值为止。例如要求768的平方根,因为252 = 625,而302 = 900,我们可先代入一猜测值26,然后迭代运算,得到较精确值:27.7128。
回到我们最开始的那个”莫名其妙”的公式,我们要求的是N的平方根,令x2 = n,假设一关于X的函数f(x)为:
f(X) = X2 - n
求f(X)的一阶导为:
f'(X) = 2X
代入前面求到的最终式中:
Xk+1 = Xk - (Xk2 - n)/2Xk
化简即得到我们最初提到的那个求平方根的神奇公式了:
![]()
用泰勒公式推导
我之前介绍过在The Art and Science of C一书中有用到泰勒公式求平方根的算法,其实牛顿迭代法也可以看作是泰勒公式(Taylor Series)的简化,先回顾下泰勒公式:

仅保留等式右边前两项:
![]()
令f(X0+ε) = 0,得到:
![]()
再令X1 = X0 + ε0,得到ε1…依此类推可知:
![]()
转化为:
![]()
引申
从推导来看,其实牛顿迭代法不仅可以用来求平方根,还可以求立方根,甚至更复杂的运算。
同样,我们还可以利用C语言来实现下那个最简单的求平方根的公式(尽管我们可以直接用sqrt()完成)
#include <stdio.h>
#include <math.h>
#define N 768
main() {
float x=1;
int i;
for (i=1;i<=1000;i++) { // recursion times : 1000
x = (x + N/x)/2;
}
printf("The square root of %d is %f/n",N,x);
}
利用牛顿迭代法求平方根
article/2025/10/1 8:17:37
相关文章
牛顿迭代法求解平方根
一个实例迭代简介牛顿迭代法 牛顿迭代法简介简单推导泰勒公式推导延伸与应用 一个实例
//java实现的sqrt类和方法
public class sqrt {public static double sqrt(double n){if (n<0) return Double.NaN;double err 1e-15;double t n;while (Math.abs(t - n/t) > err…
牛顿迭代法求一个数的平方根(python)
# !/usr/bin/env python
# -*- coding: utf-8 -*-
"""
Author: P♂boy
License: (C) Copyright 2013-2017, Node Supply Chain Manager Corporation Limited.
Contact: 17647361832163.com
Software: Pycharm
File: sqrt.py.py
Time: 2018/11/19 16:22
Desc:牛顿…
c++迭代法求平方根
用迭代法求x ,要求前后两次求出的x的差的绝对值小于10-5,求平方根的迭代公式为: 输入
一个数a。
输出 的值。
样例输入
2.0样例输出
The square root of 2.00 is 1.41421
这道题我无语了...:
#include<bits/stdc.h>
…
牛顿迭代法求平方根原理
牛顿迭代法可以求解n次方的根,但这里只讨论用它来求平方根。 牛顿迭代法求平方根过程 Java代码实现 /*** 求一个数的平方根* param number* return*/public static double squareRoot(double number){if(number < 0){ //小于0的数无法开平方return Double.NaN;}e…
【算法】牛顿迭代法求平方根及多次方根
1. 概述 牛顿迭代法 牛顿迭代法 牛顿迭代法 是非常高效的求解方程的根的方法。其求解原理可以参考各文献。大体的思路如下:
通过不断地做切线来逼近真实的根,直到误差小于精度。 可得迭代公式: x n 1 x n − f ( x n ) f ′ ( x n ) x_{…
二分法和牛顿迭代法求平方根(Python实现)
求一个数的平方根函数sqrt(int num) ,在大多数语言中都提供实现。那么要求一个数的平方根,是怎么实现的呢?
实际上求平方根的算法方法主要有两种:二分法(binary search)和牛顿迭代法(Newton iteration) 1:二分法
求根号5
a:折半…
牛顿迭代法-求平方根
牛顿迭代法 求出根号a的近似值:首先随便猜一个近似值x,然后不断令x等于x和a/x的平均数,迭代个六七次后x的值就已经相当精确了。 例如,我想求根号2等于多少。假如我猜测的结果为4,虽然错的离谱,但你可以看到…
用迭代法求某数a的平方根
今天晚上笔试题目最后一题很简单,可是自己做不出 ,就是不用库函数,求一个浮点数的平方根。
立马想到用物理法,比如正方形的面积法等,可是求解出不出,然后就绕在里面了。归根到底还是平时的知识储备太少了&…
Java基础——运行时异常和非运行时异常
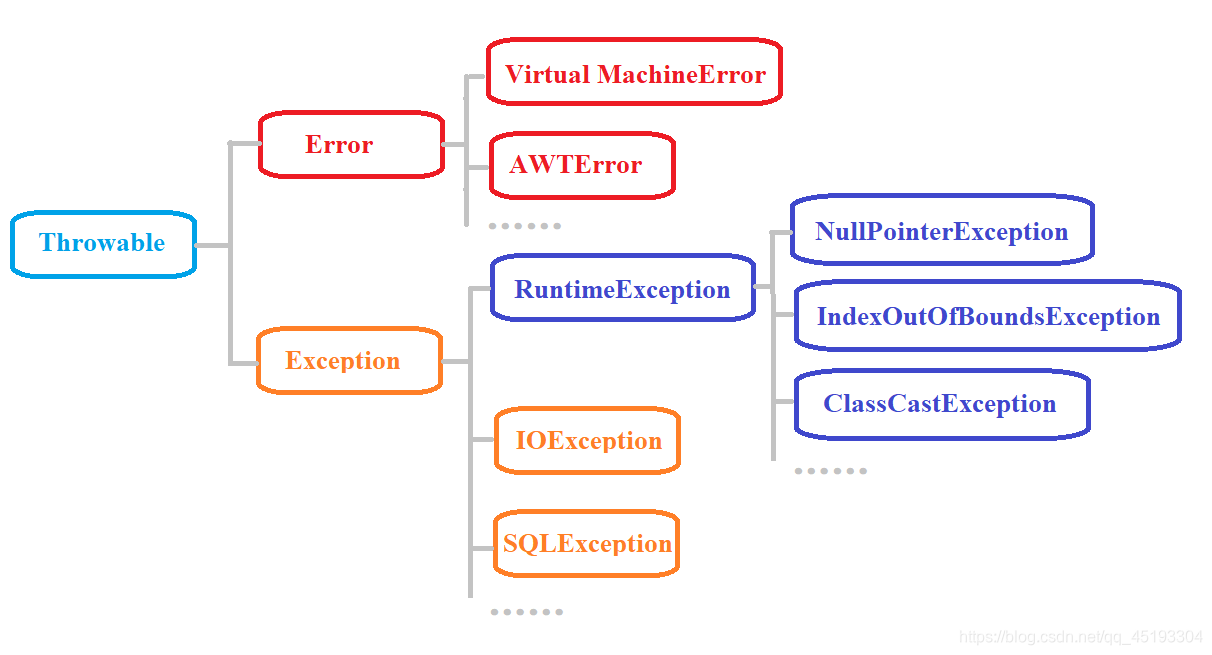
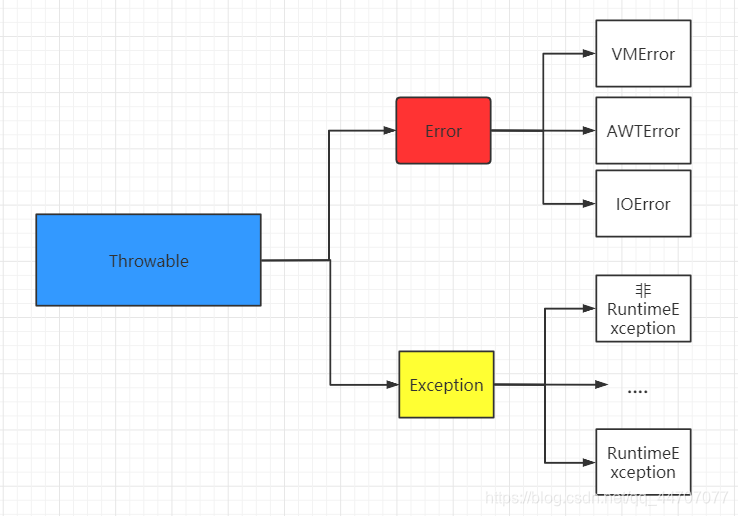
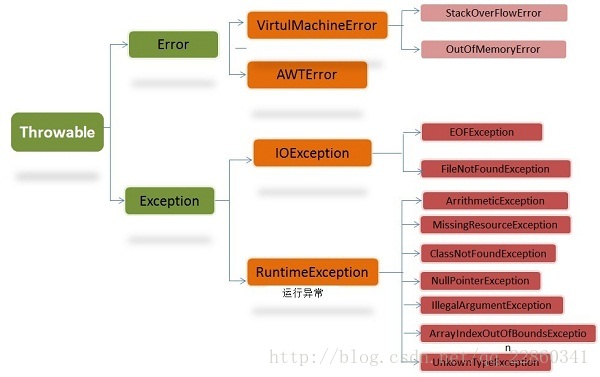
文章目录 Java中异常机制的体系结构Error(错误)Exception(异常)运行时异常和非运行时异常的区别结束 Java中异常机制的体系结构
在Java中,万物皆对象,异常也不例外。 Exception(异常࿰…
Java编译时异常与运行时异常的区别
Java的异常可以分为编译异常和运行异常,其主要区别:
编译异常要求程序员必须处理(捕获或者抛出),不然没法通过编译。
而运行异常可以不处理。
这应该是纸面最明显的区别了,我认为更重要的区别是在处理机…
运行时异常与非运行时异常有什么区别?
运行时异常与非运行时异常有什么区别?
运行时异常 RuntimeException 又称为非检查异常 uncheck exception。是 Exception 的子类。
在 Java 中,异常可以分为两种。Error 和 Exception,它们的父类是 Throwable。 Error 一些底层的类出错&…
杂谈——运行时异常和普通异常有什么区别
说到异常,大家都熟悉,只要程序出错了,那么肯定会说:“哎呀,我的程序出错啦~它抛出异常啦”。
但单单以“异常”的名称来称呼它们,未免也太粗糙了。我们毕竟是一个精致的程序员,当然得知道他们到…
常见的编译时异常和运行时异常
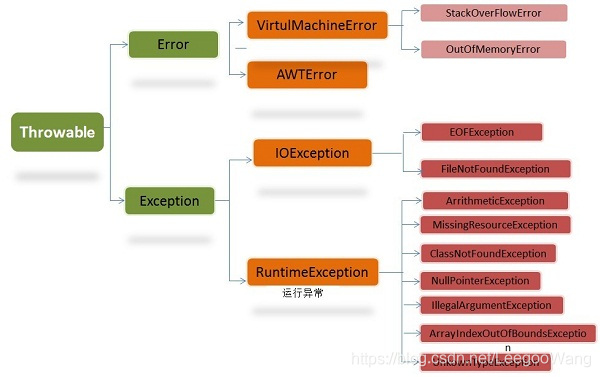
常见的编译时异常和运行是异常
1、粉红色的是编译时异常 2、绿色的异常是运行时异常 3、声明为Error的,则属于严重错误,如系统崩溃、虚拟机错误、动态链接失败等,这些错误无法恢复或者不可能捕捉,将导致应用程序中断,…
浅谈Java异常及其编译时异常和运行时异常的区别
异常是程序编码和运行时经常发生的事件,了解异常有助于我们提高代码质量,增强系统的健壮性,这里总结一下Java编程中的异常、以及Java编译时异常和运行时异常的区别,并列举几种常见的异常,以供参考学习。
一、什么是异…
Java 运行时异常和非运行时异常
异常类型分为两类:运行时异常和非运行时异常。
一、运行时异常:
运行时异常(RuntimeException),一般不需要程序员进行捕获。
例如:NullPointException,IndexOutOfBoundsException。如果不对该…
Java-异常处理(编译时异常、运行时异常及处理机制,自定义异常)
个人简介 大家好,我是翰慧腾。一名正在努力学JAVA的大一小白,本文章为初学的笔记,希望各位多多指教。💙欢迎点赞收藏留言💜你要批评指点四周风景,首先你要爬上屋顶🧡 一、异常
概述:…
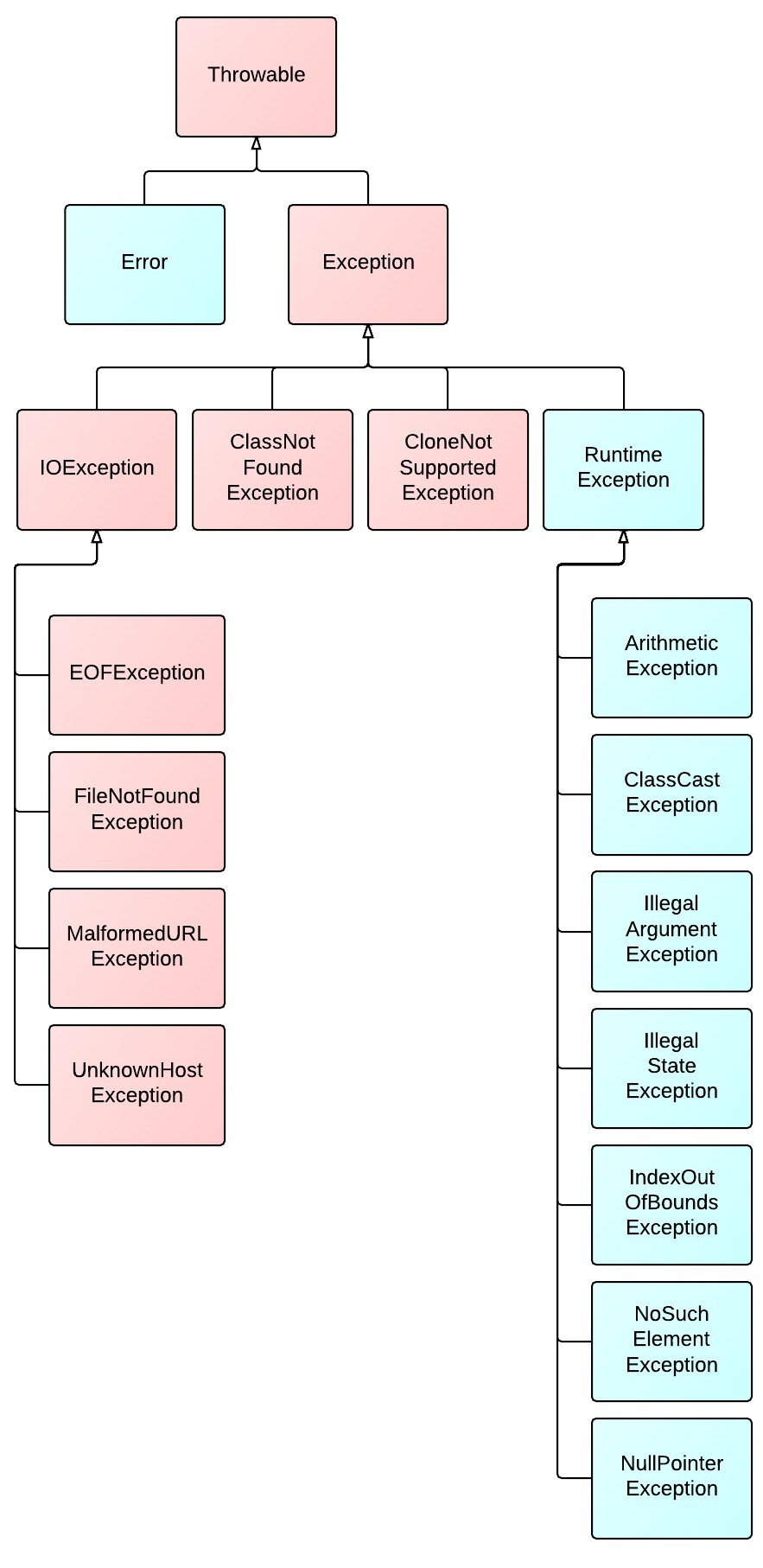
通俗理解运行时异常和非运行时异常(一般异常)
一,异常的概念 Java异常类层次结构图: Throwable: 有两个重要的子类:Exception(异常)和 Error(错误),二者都是 Java 异常处理的重要子类,各自都包含大量子类…
运行时异常与检查异常区别
首先,思考一个问题,看下面三个代码,当抛出异常时,后面的代码还会运行吗,是否要在异常后加上return语句?
//代码1
public static void test() throws Exception {throw new Exception("参数越界"…
编译时异常与运行时异常
在实际开发中,经常会在程序编译时产生一些异常,必须要对这些异常进行处理,这种异常称为编译时异常,也称为checked异常。另外,还有一种异常是在程序运行时产生的,这种异常即使不编写异常处理代码,…