相关概念

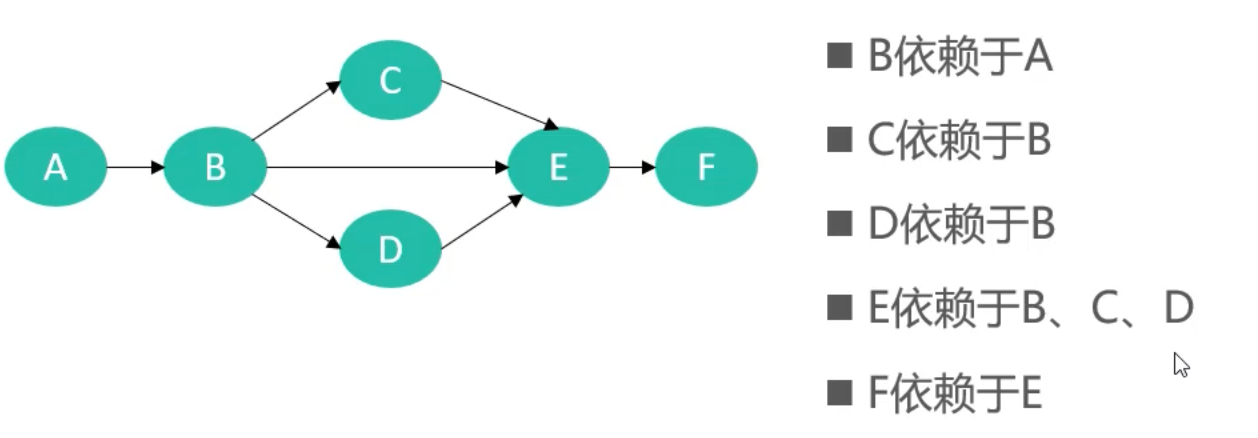
AOV网

• 一项大的工程常被分为多个小的子工程
  • 子工程之间可能存在一定的先后顺序，即某些子工程必须在其他的一些子工程完成后才能开始
• 在现代化管理中,人们常用有向图来描述和分析一项工程的计划和实施过程，子工程被称为活动(Activity)
  • 以顶点表示活动、有向边表示活动之间的先后关系，这样的图简称为AOV网
• 标准的AOV网必须是一个有向无环图(Directed Acyclic Graph, 简称 DAG)

拓扑排序

• 前驱活动: 有向边起点的活动称为终点的前驱活动
  • 只有当一个活动的前驱全部都完成后，这个活动才能进行
• 后继活动: 有向边终点的活动称为起点的后继活动

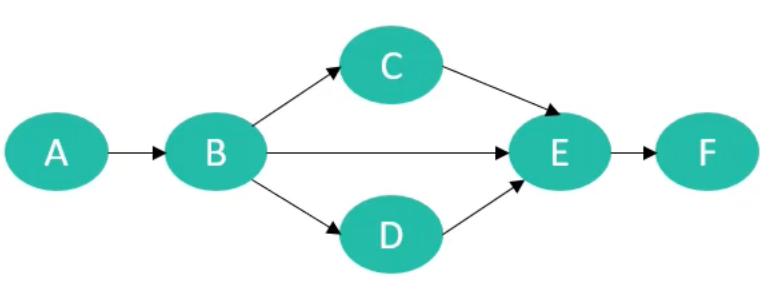
• 什么是拓扑排序?
  • 将AOV网中所有活动排成一个序列，使得每个活动的前驱活动都排在该活动的前面
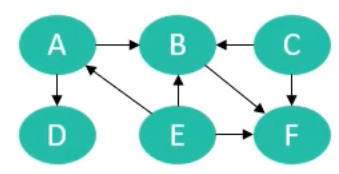
  • 比如上图的拓扑排序结果是: A、B、C、D、E、F或者是A、B、D、C、E、F(结果并不一定是唯一的)

实现思路

• 可以使用卡恩算法(kahn于1962年提出)完成拓扑排序
• 假设L是存放拓扑排序结果的列表

1. 把所有入度为0的顶点放入L中，然后把这些顶点从图中去掉
2. 重复操作1，直到找不到入度为0的顶点

• 如果此时L中的元素个数和顶点总数相同，说明拓扑排序完成
• 如果此时L中的元素个数少于顶点总数，说明原图中存在环，无法进行拓扑排序

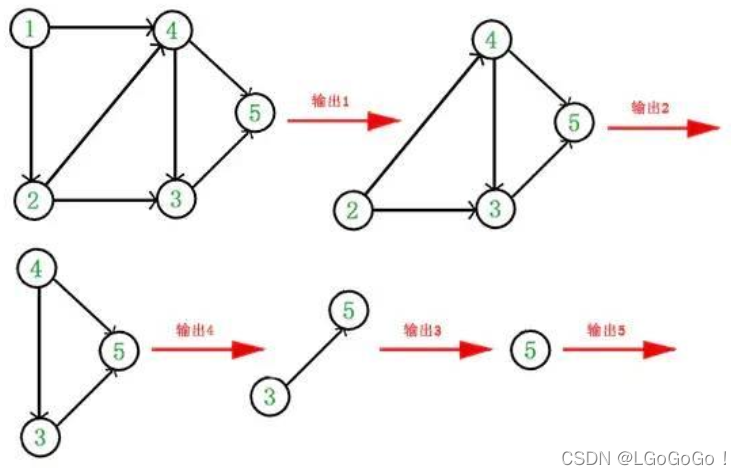
实现过程

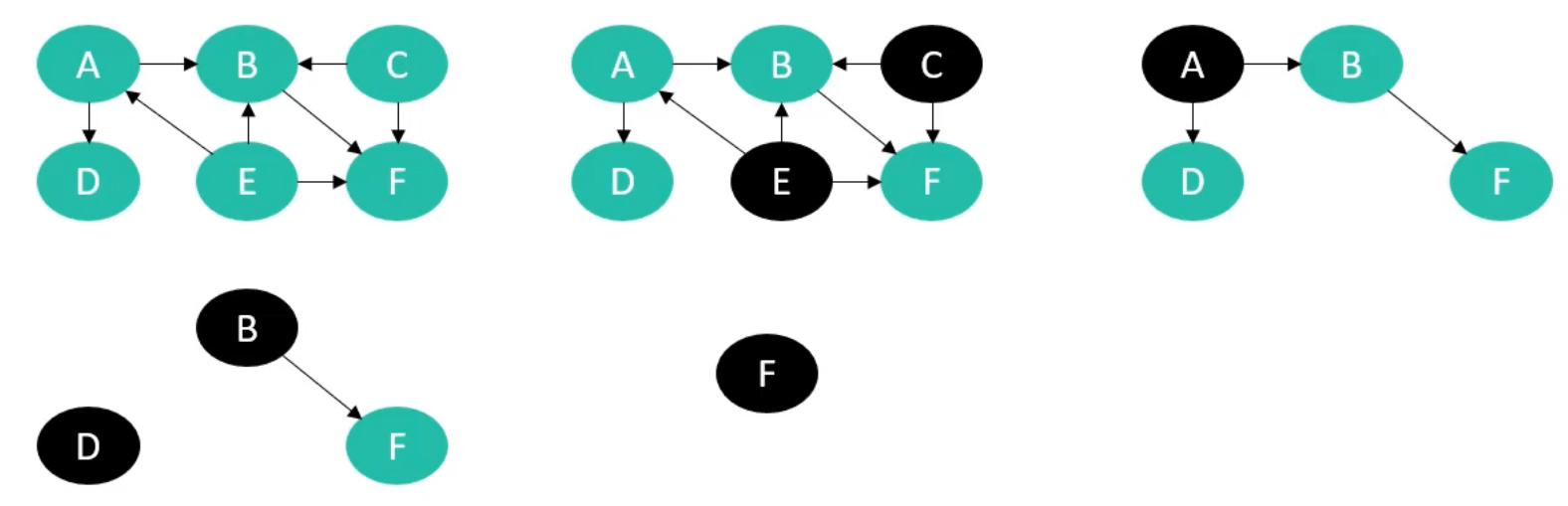
• 首先维护一张入度表和一个list集合,和一个队列
  入度表
  
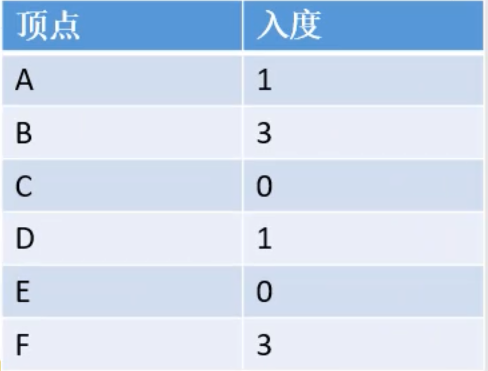
  队列(初始化将所有的入度为0的顶点放到队列中)
  

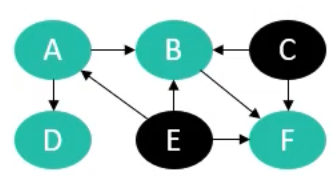
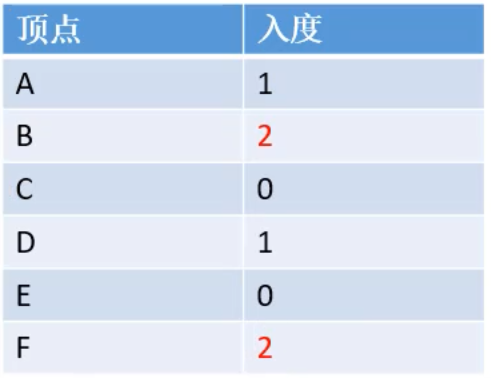
• 将C出队,放到list中,并且遍历所有以C为为起点的边的终点的集合,将这些点的入度-1,如果这些点中存在-1之后入度为0的点，将其加入到队列中。
  
  
  

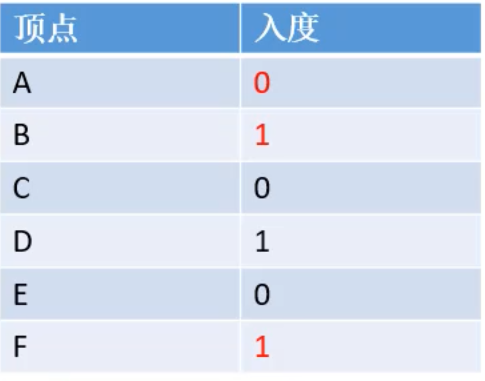
• 将队列中的顶点E出队,放到list中,并且遍历所有以E为为起点的边的终点的集合,将这些点的入度-1, 此轮-1后，点A的入度为0，入队
  
  
  
  
  
  

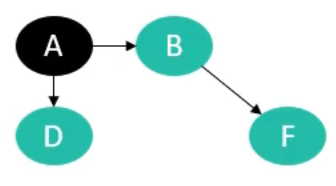
• A点出队,放到list集合中,以A点为起点的边的终点集合的入度-1,此轮之后,B,D两点的入度为0,加入到队列中
  

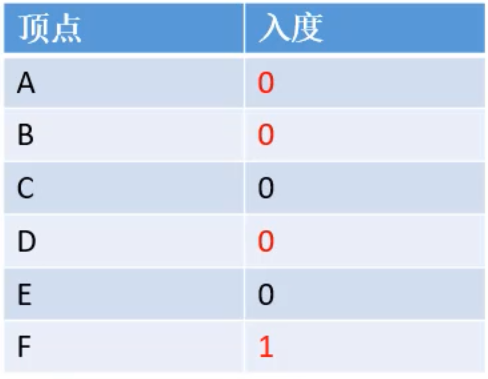
• D点出队,加入list集合中
  
  

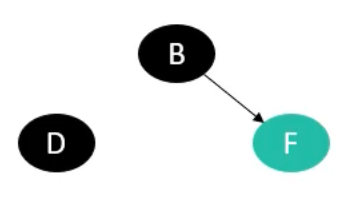
• B点出队,加入到list集合中,更新入度表,点F入队
  

• 点F出队，加入到list集合中
  
  

代码

• 图的接口类

public interface Graph<V, E> {/*** 打印边*/void print();/*** 边的数量* @return*/int edgeSize();/*** 顶点的数量* @return*/int vertexSize();/*** 添加顶点* @param v*/void addVertex(V v);/*** 添加边(无权值)* @param from* @param to*/void addEdge(V from, V to);/*** 添加边(有权值)* @param from* @param to* @param weight*/void addEdge(V from, V to, E weight);/*** 移除顶点* @param v*/void removeVertex(V v);/*** 移除边* @param from* @param to*/void removeEdge(V from, V to);/*** 拓扑排序* @return*/List<V> topologicalSort();}

• 图的实现类

public class ListGraph<V, E> implements Graph<V, E> {private Map<V, Vertex<V, E>> vertices = new HashMap<>();private Set<Edge<V, E>> edges = new HashSet<>();/*** 打印*/@Overridepublic void print() {//打印顶点vertices.forEach((v, vertex) -> {System.out.println(v);System.out.println("out-----------");System.out.println(vertex.outEdges);System.out.println("in------------");System.out.println(vertex.inEdges);});//打印边edges.forEach(edge -> System.out.println(edge));}@Overridepublic int edgeSize() {return edges.size();}@Overridepublic int vertexSize() {return vertices.size();}@Overridepublic void addVertex(V v) {if (vertices.containsKey(v)) {return;}//添加顶点vertices.put(v, new Vertex<>(v));}@Overridepublic void addEdge(V from, V to) {addEdge(from, to, null);}@Overridepublic void addEdge(V from, V to, E weight) {Vertex<V, E> fromVertex = vertices.get(from);//如果map中不存在value=from的顶点,则创建并放到map中if (fromVertex == null) {fromVertex = new Vertex<>(from);vertices.put(from, fromVertex);}//如果map中不存在value=to的顶点,则创建并放到map中Vertex<V, E> toVertex = vertices.get(to);if (toVertex == null) {toVertex = new Vertex<>(to);vertices.put(to, toVertex);}//根据两个顶点创建边Edge<V, E> edge = new Edge<>(fromVertex, toVertex);//赋权值edge.weight = weight;//如果edge这条边已存在,就删除edge这条边,在from顶点的outEdges集合中删掉这条边,在to顶点的inEdges集合中删除这条边,直接删除原来的边,重新添加新的边,因为权值可能更新了。if (fromVertex.outEdges.remove(edge)) {toVertex.inEdges.remove(edge);}//再次把边添加到两个顶点的两个集合中。fromVertex.outEdges.add(edge);toVertex.inEdges.add(edge);//将边添加到集合edges中edges.add(edge);}@Overridepublic void removeVertex(V v) {Vertex<V, E> vertex = vertices.remove(v);//如果map中不存在value=v的顶点,直接返回if (vertex == null) {return;}//删除边集和Edges中的所有和顶点vertex相关的边for (Iterator<Edge<V, E>> iterator = vertex.outEdges.iterator(); iterator.hasNext();) {Edge<V, E> edge = iterator.next();edge.to.inEdges.remove(edge);iterator.remove();edges.remove(edge);}for (Iterator<Edge<V, E>> iterator = vertex.inEdges.iterator(); iterator.hasNext();) {Edge<V, E> edge = iterator.next();edge.from.outEdges.remove(edge);iterator.remove();edges.remove(edge);}}@Overridepublic void removeEdge(V from, V to) {Vertex<V, E> fromVertex = vertices.get(from);//如果map中不存在value=from的顶点,则肯定也没有以from为顶点的边if (fromVertex == null) {return;}//如果map中不存在value=to的顶点,则肯定也没有以to为顶点的边Vertex<V, E> toVertex = vertices.get(to);if (toVertex == null) {return;}//根据两个顶点创建边Edge<V, E> edge = new Edge<>(fromVertex, toVertex);//删除对应的边if (fromVertex.outEdges.remove(edge)) {toVertex.inEdges.remove(edge);edges.remove(edge);}}/*** 顶点*/static class Vertex<V, E> {V value;Set<Edge<V, E>> inEdges = new HashSet<>();Set<Edge<V, E>> outEdges = new HashSet<>();public Vertex(V value) {this.value = value;}@Overridepublic boolean equals(Object o) {if (this == o) {return true;}if (o == null || getClass() != o.getClass()) {return false;}Vertex<V, E> vertex = (Vertex<V, E>) o;return Objects.equals(value, vertex.value);}@Overridepublic int hashCode() {return Objects.hash(value);}@Overridepublic String toString() {return value == null ? "null" : value.toString();}}@Overridepublic List<V> topologicalSort() {//拓扑排序后的结果List<V> list =new ArrayList<>();Queue<Vertex<V,E>> queue = new LinkedList<>();//使用map维护每个顶点的出度Map<Vertex<V, E>, Integer> ins = new HashMap<>();vertices.forEach((v, vertex) -> {//获取以vertex为终点的边的个数,即入度大小int in = vertex.inEdges.size();//如果入度为0，放到队列中,否则将顶点的入度放到map(顶点 -> 顶点的入度)中if (in == 0) {queue.offer(vertex);} else {ins.put(vertex, in);}});//当队列非空while (!queue.isEmpty()) {//队列元素出队Vertex<V, E> vertex = queue.poll();//放入返回结果中list.add(vertex.value);//遍历所有以该顶点为起点的边的集合,将边的重点的度for (Edge<V, E> edge : vertex.outEdges) {//终点的入度-1int toIn = ins.get(edge.to) - 1;//入度为0加入队列,否则更新map中维护的顶点的入度if (toIn == 0) {queue.offer(edge.to);} else {ins.put(edge.to, toIn);}}}return list;}/*** 边*/static class Edge<V, E> {Vertex<V, E> from;Vertex<V, E> to;E weight;public Edge(Vertex<V, E> from, Vertex<V, E> to) {this.from = from;this.to = to;}@Overridepublic boolean equals(Object o) {if (this == o) {return true;}if (o == null || getClass() != o.getClass()) {return false;}Edge<V, E> edge = (Edge<V, E>) o;return Objects.equals(from, edge.from) && Objects.equals(to, edge.to);}@Overridepublic int hashCode() {return Objects.hash(from, to);}@Overridepublic String toString() {return "Edge{" +"from=" + from +", to=" + to +", weight=" + weight +'}';}}}

测试

测试类

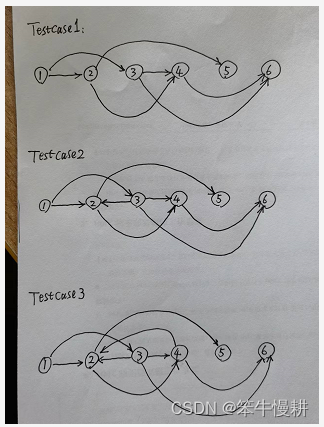
public class TopologicalSort {public static final Object[][] TOPO = {{0, 2},{1, 0},{2, 5}, {2, 6},{3, 1}, {3, 5}, {3, 7},{5, 7},{6, 4},{7, 6}};/*** 生成有向图*/private static Graph<Object, Double> directedGraph(Object[][] data) {Graph<Object, Double> graph = new ListGraph<>();for (Object[] edge : data) {if (edge.length == 1) {graph.addVertex(edge[0]);} else if (edge.length == 2) {graph.addEdge(edge[0], edge[1]);}}return graph;}public static void main(String[] args) {//构建有向图Graph<Object, Double> graph = directedGraph(TOPO);//对图进行拓扑排序List<Object> list = graph.topologicalSort();System.out.println(list);}}

测试样例

• 构造的图如下图所示
  
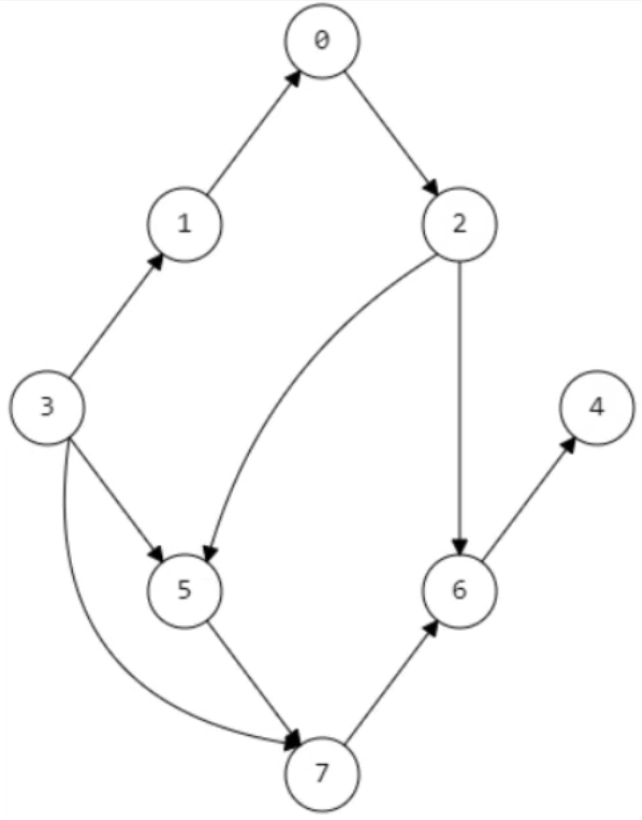
• 排序的输出结果