一、拓扑排序简介

1.Topological Sorting，指的是一个DAG(Directed Acyclic Graph)即有向图所有顶点满足一定条件的线性序列。

拓扑序列应满足两个条件：

每个点都只出现一次
如果存在一条从A指向B的边，那么A点在序列中出现的顺序应该在B点之前。

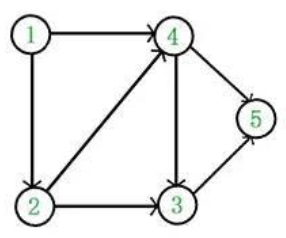
在这里插入图片描述
2.算法原理：

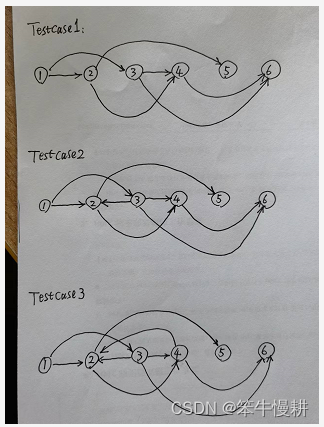
①从 DAG 图中选择一个没有前驱（即入度为0）的顶点并输出。
②从图中删除该顶点和所有以它为起点的有向边。
③重复 1 和 2 直到当前的 DAG 图为空或当前图中不存在无前驱的顶点为止。

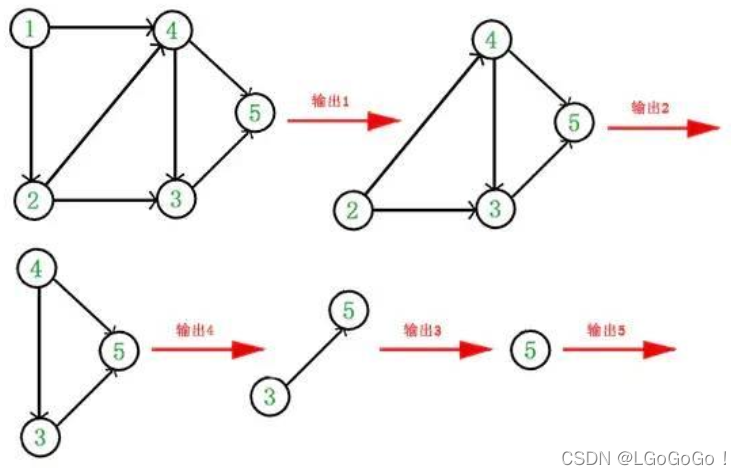
在这里插入图片描述
得到拓扑排序后的结果是 { 1, 2, 4, 3, 5 }

3.注意事项：
①非DAG图没有拓扑排序一说
②拓扑排序的情况可能是不唯一的

二、例题

1.题目

课程表 II

跳转LeetCode

现在你总共有 numCourses 门课需要选，记为 0 到 numCourses - 1。给你一个数组 prerequisites ，其中 prerequisites[i] = [ai, bi] ，表示在选修课程 ai 前必须先选修 bi 。

例如，想要学习课程 0 ，你需要先完成课程 1 ，我们用一个匹配来表示：[0,1] 。
返回你为了学完所有课程所安排的学习顺序。可能会有多个正确的顺序，你只要返回任意一种就可以了。如果不可能完成所有课程，返回一个空数组。

示例 1：
输入：numCourses = 2, prerequisites = [[1,0]]
输出：[0,1]
解释：总共有 2 门课程。要学习课程 1，你需要先完成课程 0。因此，正确的课程顺序为 [0,1] 。

示例 2：
输入：numCourses = 4, prerequisites = [[1,0],[2,0],[3,1],[3,2]]
输出：[0,2,1,3]
解释：总共有 4 门课程。要学习课程 3，你应该先完成课程 1 和课程 2。并且课程 1 和课程 2 都应该排在课程 0 之后。
因此，一个正确的课程顺序是 [0,1,2,3] 。另一个正确的排序是 [0,2,1,3] 。

示例 3：
输入：numCourses = 1, prerequisites = []
输出：[0]

2.分析

参考文章

①DFS形式：
课程之间的依赖关系抽象成有向边，那么这幅图的拓扑排序结果就是上课顺序。

首先，我们先判断一下题目输入的课程依赖是否成环，成环的话是无法进行拓扑排序的，所以我们可以复用 “课程表I” 的主函数，之后将后序遍历的结果进行反转，就是拓扑排序的结果。

在编码层面，问题则转化为：由所给数组构建图 → 图的后序遍历 → 判断图中是否存在环 → 翻转后序遍历序列

②BFS形式：

1、构建邻接表，和之前一样，边的方向表示「被依赖」关系。
2、构建一个 indegree 数组记录每个节点的入度，即 indegree[i] 记录节点 i 的入度。以及用于存储从图中被弹出的节点的数组 ans。
3、对 BFS 队列进行初始化，将入度为 0 的节点首先装入队列。
4、开始执行 BFS 循环，不断弹出队列中的节点，加入 ans 中，减少相邻节点的入度，并将入度变为 0 的节点加入队列。
5、如果最终所有节点都被遍历过（count 等于节点数），则说明不存在环，反之则说明存在环。
6、若不存在环，则可直接返回数组。

3.代码

①DFS答案代码：

package Graph;import java.util.ArrayList;
import java.util.Collections;
import java.util.LinkedList;
import java.util.List;/*** @author: LYZ* @date: 2022/3/24 18:51* @description: 210. 课程表 II*/
public class FindOrder {public static void main(String[] args) {int numCourses = 4;int[][] prerequisites = {{1, 0}, {2, 0}, {3, 1}, {3, 2}};FindOrder findOrder = new FindOrder();int[] ans = findOrder.findOrder(numCourses, prerequisites);for (int n : ans) {System.out.println(n);}}public int[] findOrder(int numCourses, int[][] prerequisites) {List<Integer>[] graph = buildGraph(numCourses, prerequisites);visited = new boolean[numCourses];onPath = new boolean[numCourses];for (int i = 0; i < numCourses; i++) {traverse(graph, i);}//以下是新添语句// 有环图无法进行拓扑排序if (hasCycle) {return new int[]{};}//反转后序遍历结果即为拓扑排序结果Collections.reverse(postorder);int[] ans = new int[numCourses];for (int i = 0; i < numCourses; i++) {ans[i] = postorder.get(i);}return ans;}List<Integer>[] buildGraph(int numCourses, int[][] prerequisites) {// 图中共有 numCourses 个节点List<Integer>[] graph = new LinkedList[numCourses];for (int i = 0; i < numCourses; i++) {graph[i] = new LinkedList<>();}for (int[] edge : prerequisites) {int from = edge[1], to = edge[0];// 添加一条从 from 指向 to 的有向边// 边的方向是「被依赖」关系，即修完课程 from 才能修课程 tograph[from].add(to);}return graph;}List<Integer> postorder = new ArrayList<>();boolean[] visited;boolean[] onPath;boolean hasCycle = false;void traverse(List<Integer>[] graph, int s) {if (onPath[s]) {hasCycle = true;}if (visited[s] || hasCycle) {return;}visited[s] = true;onPath[s] = true;for (int n : graph[s]) {traverse(graph, n);}postorder.add(s); //相较于课程表I增加的语句onPath[s] = false;}
}

②BFS答案代码:

package Graph;import java.util.*;/*** @author: LYZ* @date: 2022/3/24 18:51* @description: 210. 课程表 II*/
public class FindOrder {public static void main(String[] args) {int numCourses = 4;int[][] prerequisites = {{1, 0}, {2, 0}, {3, 1}, {3, 2}};FindOrder findOrder = new FindOrder();int[] ans = findOrder.findOrder(numCourses, prerequisites);for (int n : ans) {System.out.println(n);}}//BFS法public int[] findOrder(int numCourses, int[][] prerequisites) {// 建图，有向边代表「被依赖」关系List<Integer>[] graph = buildGraph(numCourses, prerequisites);List<Integer> list = new ArrayList<>();int[] ans = new int[numCourses];// 构建入度数组int[] indegree = new int[numCourses];for (int[] edge : prerequisites) {int from = edge[1], to = edge[0];// 节点 to 的入度加一indegree[to]++;}// 根据入度初始化队列中的节点Queue<Integer> q = new LinkedList<>();for (int i = 0; i < numCourses; i++) {if (indegree[i] == 0) {// 节点 i 没有入度，即没有依赖的节点// 可以作为拓扑排序的起点，加入队列q.offer(i);}}// 记录遍历的节点个数int count = 0;// 开始执行 BFS 循环while (!q.isEmpty()) {// 弹出节点 cur，并将它指向的节点的入度减一int cur = q.poll();list.add(cur);count++;for (int next : graph[cur]) { //graph[cur]是由cur节点指向的所有节点构成的List集合indegree[next]--; //indegree是存储所有节点入度值的数组if (indegree[next] == 0) {// 如果入度变为 0，说明 next 依赖的节点都已被遍历q.offer(next);}}}if (count != numCourses) {return new int[]{};}for (int i = 0; i < numCourses; i++) {ans[i] = list.get(i);}return ans;}// 建图函数List<Integer>[] buildGraph(int numCourses, int[][] prerequisites) {// 图中共有 numCourses 个节点List<Integer>[] graph = new LinkedList[numCourses];for (int i = 0; i < numCourses; i++) {graph[i] = new LinkedList<>();}for (int[] edge : prerequisites) {int from = edge[1], to = edge[0];// 添加一条从 from 指向 to 的有向边// 边的方向是「被依赖」关系，即修完课程 from 才能修课程 tograph[from].add(to);}return graph;}
}

记录拓扑排序结果我处理的不好，额外声明了一个集合。题解的代码，利用用于判断图中是否有环的计数器，作为 ans 数组的下标，很巧妙。

    // 记录拓扑排序结果int[] res = new int[numCourses];// 记录遍历节点的顺序（索引）int count = 0;// 开始执行 BFS 算法while (!q.isEmpty()) {int cur = q.poll();// 弹出节点的顺序即为拓扑排序结果res[count] = cur;count++;for (int next : graph[cur]) {indgree[next]--;if (indgree[next] == 0) {q.offer(next);}}}