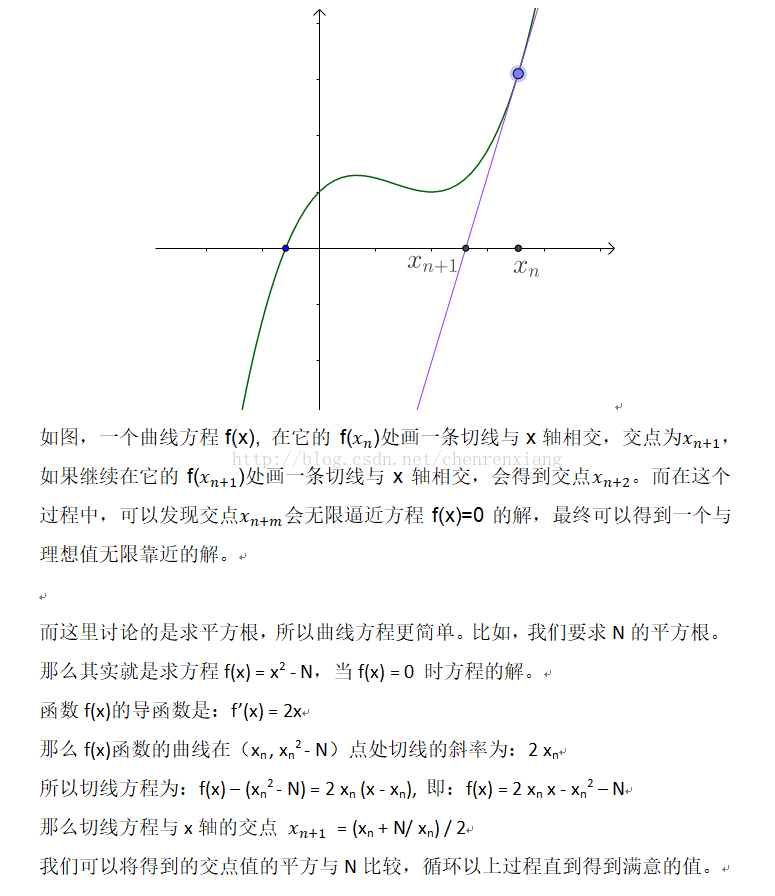
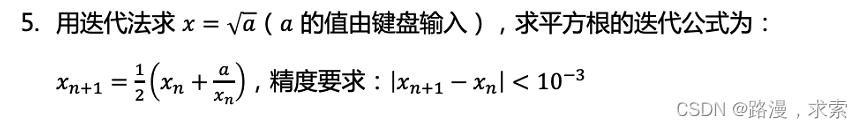前置知识
有向无环图
在图论中,如果一个有向图无法从某个顶点出发经过若干条边回到该点,则这个图是一个有向无环图(DAG图)。
如图所示。

入度
对于一个有向图,若x点指向y点,则称x点为y点的入度。
出度
对于一个有向图,若x点指向y点,则称y点为x点的出度。
队列
队列是一种特殊的线性表,特殊之处在于它只允许在表的前端(front)进行删除操作,而在表的后端(rear)进行插入操作,和栈一样,队列是一种操作受限制的线性表。进行插入操作的端称为队尾,进行删除操作的端称为队头。
我们可以用双指针标记一下,通过front指针与rear指针,对队头和队尾进行标记,然后只允许在front、rear指针的位置进行增删改查,那么这样便实现了对数组的受限。这是一种运用数组的数据结构对队列的模拟。初学者建议先用这种方式熟悉队列。
具体操作:
/*通常将front赋值为0,rear赋值为-1方便后续进队、出队以及取队首元素*/
int a[100], front=0, rear=-1;// 进队
a[++rear] = 10;// 出队
front++// 取队首元素
a[front]// 取队尾元素
a[rear]// 判断是否为空队
if(front > rear)cout << "该队列为空队";
不过,到了后期,为了节省时间,我们可以直接用c++自带的STL容器来完成操作。
具体操作如下:
// 导入queue包
#include<queue>// 申明一个queue对象
// 填入你想装填的数据类型
queue<int> qu;// 进队
int a = 10;
qu.push(a);// 出队,无返回值
qu.pop();// 取队首元素
int front = qu.front();
概述
今天我们来学拓扑排序
什么是拓扑排序呢?
百度百科这样说:
对一个有向无环图(Directed Acyclic Graph简称DAG)G进行拓扑排序,是将G中所有顶点排成一个线性序列,使得图中任意一对顶点u和v,若边<u,v>∈E(G),则u在线性序列中出现在v之前。通常,这样的线性序列称为满足拓扑次序(Topological Order)的序列,简称拓扑序列。简单的说,由某个集合上的一个偏序得到该集合上的一个全序,这个操作称之为拓扑排序。
什么意思呢?
俗话说的好:
实践是真理的试金石
那么,就让我们举一个例子吧!
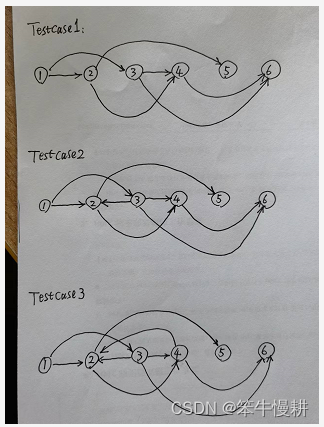
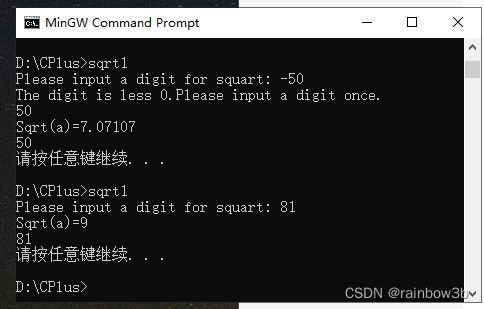
如图,1、2、3、4、5几个点组成了一个图。

那么,1,2,4,3,6,5或1,2,4,3,5,6就是它的拓扑序
但是,这是如何实现的呢?请看下面的算法原理。
算法原理
下面我将使用图文结合的方式演示拓扑排序的算法原理。
还是上面那张图。

首先,将入度为0的点入队。上图中是点1。

然后,用宽搜遍历队列。
对每个点的每轮遍历步骤如下:
- 将这个点出队,并加入拓扑数组中
- 遍历这个点的所有出度
- 将其出度点的入度数量减少一
- 如果其出度点入度为0,入队
那么,一轮下来,就变成这样子了:

以此类推。
遍历到点3时,是这样的:

……
然后,就没有然后了,一切结束。

如图所示,其拓扑序为1,2,4,3,5,6。当然,也可以是1,2,4,3,6,5。
算法实现
这可以变为以下的问题。我称为拓扑排序元问题。
给你一个有向无环图,请输出它的拓扑序(m条有向边,n个结点)
建图(邻接表存图)
首先,我们要建图
这里采用邻接表建图。
邻接表是什么?
以点为一个结点,用其邻接点建表
怎么这么朦胧?好吧,偷懒了,自己查百度……
看到这里,就默认你会了建图操作。那么,放一下代码。
(此处设定为m条有向边)
for(int i=1;i<=m;i++)
{int x,y;scanf("%d%d",&x,&y);rd[y]++;e[x].push_back(y);
}
rd[y]++ 是什么意思?请往后看。
入队
上面提到,首先,将入度为0的点入队。
那么,我们就遍历一遍n个点,当遇到入度为0的点时,入队。
如何判断入度为0?
这时前面的 rd数组 就有用了。它是用于统计入度数的。
而前面为何是rd[y]++?
因为是 x指向y,因此y入度数加1
入队操作
非常简单!这里为了省力,用了STL容器
只需要**q.push(i)**一下就可以了
代码
queue<int>q;for(int i=1;i<=n;i++){if(rd[i]==0) q.push(i);//入度为0,入队 }
核心部分
这部分的过程,我在前面是这样说的:
用宽搜遍历队列。
那就宽搜。
宽搜
没遍历到一个点,就将其弹出,并压入拓扑数组。
对每个点的操作
我在前面这样说:
对每个点的每轮遍历步骤如下:
1.将这个点出队,并加入拓扑数组中
2.遍历这个点的所有出度
3.将其出度点的入度数量减少一
4.如果其出度点入度为0,入队
那就照着做嘛。
很简单,实在看不懂代码中有注释。
代码
while(!q.empty()){int x=q.front();q.pop();topu.push_back(x);//推入拓扑数组 for(auto y:e[x]){rd[y]--;//删掉一条边 if(rd[y]==0)//入度为0 {q.push(y);//入队 }}}
好,大功告成!
算法元代码
上面没看懂的话,看下面的代码,含有注释。
#include<bits/stdc++.h>
using namespace std;
const int NN=5005;
int n,m,rd[NN];
//rd[i]表示i点的入度数
vector<int>e[NN],topu;
//e作为邻接表存储用,topu储存拓扑序
void tuopu()
{queue<int>q;for(int i=1;i<=n;i++){if(rd[i]==0) q.push(i);//入度为0,入队 }while(!q.empty()){int x=q.front();q.pop();topu.push_back(x);//推入拓扑数组 for(auto y:e[x]){rd[y]--;//删掉一条边 if(rd[y]==0)//入度为0 {q.push(y);//入队 }}}
}
int main()
{scanf("%d%d",&n,&m);for(int i=1;i<=m;i++){int x,y;scanf("%d%d",&x,&y);rd[y]++;//x指向y,因此y入度数加1 e[x].push_back(y);//加边 }tuopu();for(auto x:topu){printf("%d ",x);//输出拓扑序 }
}
总结
拓扑排序就是这回事:
首先,将入度为0的点入队。
然后,用宽搜遍历队列。
在此之后,对每个点进行如下操作:
1.将这个点出队,并加入拓扑数组中
2.遍历这个点的所有出度
3.将其出度点的入度数量减少一
4.如果其出度点入度为0,入队
下一篇文章,我将会详细讲解拓扑排序相关例题。
好,期待三连~~