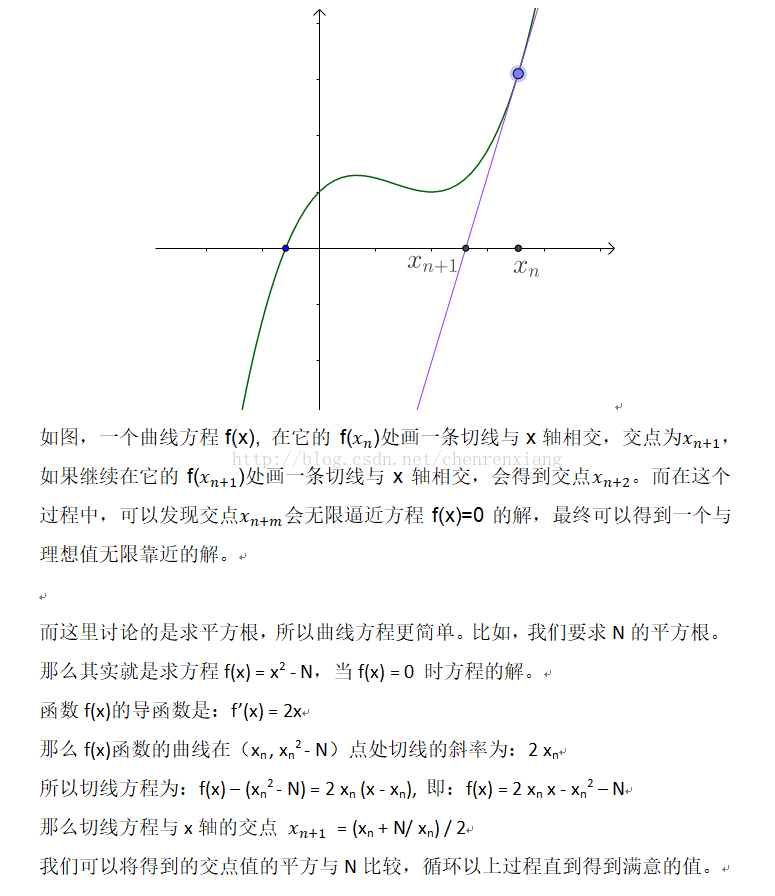
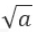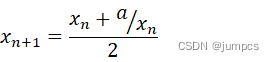拓扑排序

article/2025/10/1 7:53:39

拓扑排序

一、拓扑排序的定义：

先引用一段百度百科上对于拓扑排序的定义：

对一个有向无环图 ( Directed Acyclic Graph 简称 DAG ) G 进行拓扑排序，是将 G
中所有顶点排成一个线性序列，使得图中任意一对顶点 u 和 v ，若边 < u , v > ∈ E ( G )，则 u 在线性序列中出现在 v
之前。通常，这样的线性序列称为满足拓扑次序 ( Topological Order )
的序列，简称拓扑序列。简单的说，由某个集合上的一个偏序得到该集合上的一个全序，这个操作称之为拓扑排序。

什么意思呢，总结起来有三个要点：
1.有向无环图；
2.序列里的每一个点只能出现一次；
3.任何一对 u 和 v ，u 总在 v 之前（这里的两个字母分别表示的是一条线段的两个端点，u 表示起点，v 表示终点）；

二、拓扑排序的过程

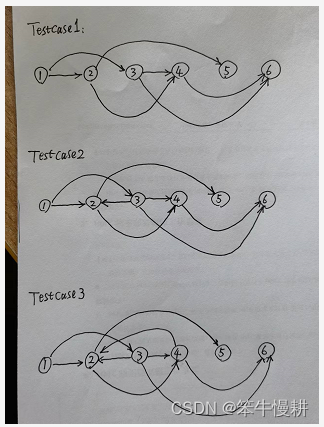
这里以下面这个有向无环图为例，分析一下拓扑排序的具体过程。
在这里插入图片描述

首先，我举一个例子，比如打游戏时，刚开始一个游戏，你一定要先打第一关，因为只有打通了第一关，才能解锁下一关或下几关，而不能上来就打第二关。特别地，第一关时不需要之前打任何一关，最后一关打完不会解锁任何一关。
回到图中我举的例子，1 号端点就相当于第一关，而 6 号端点就相当于是最后一关。所以我们就知道了：
1.找一个入度为零（不需其他关卡通关就能解锁的）的端点，如果有多个，则从编号小的开始找；
2.将该端点的编号输出；
3.将该端点删除，同时将所有由该点出发的有向边删除；
4.循环进行 2 和 3 ，直到图中的图中所有点的入度都为零；
5.拓扑排序结束；

那么我现在就以上图为例，详细分析一下过程；

第一步：输出 “ 1 ”；
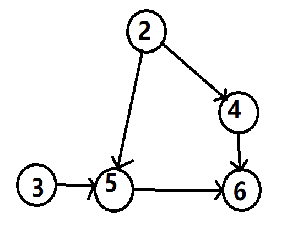
在这里插入图片描述

第二步：输出 “ 2 ”；
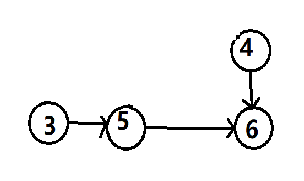
在这里插入图片描述
第三步：输出 “ 3 ”；

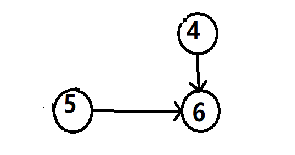
第四步：输出 “ 4 ”；

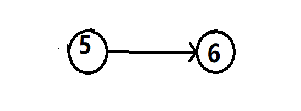
第五步：输出 “ 5 ”；

第六步：输出 “ 6 ”，排序结束。
所以，最终拓扑排序的结果是
1 2 3 4 5 6
三、拓扑排序在具体题目中应用

下面以最大食物链计数为例实际应用一下拓扑排序。

题目背景
你知道食物链吗？Delia生物考试的时候，数食物链条数的题目全都错了，因为她总是重复数了几条或漏掉了几条。于是她来就来求助你，然而你也不会啊！写一个程序来帮帮她吧。

题目描述
给你一个食物网，你要求出这个食物网中最大食物链的数量。

（这里的“最大食物链”，指的是生物学意义上的食物链，即最左端是不会捕食其他生物的生产者，最右端是不会被其他生物捕食的消费者。）

Delia 非常急，所以你只有 11 秒的时间。

由于这个结果可能过大，你只需要输出总数模上 8011200280112002 的结果。

输入格式
第一行，两个正整数 n、mn、m，表示生物种类 nn 和吃与被吃的关系数 mm。

接下来 mm 行，每行两个正整数，表示被吃的生物A和吃A的生物B。

输出格式
一行一个整数，为最大食物链数量模上 8011200280112002 的结果。

输入输出样例
输入
5 7
1 2
1 3
2 3
3 5
2 5
4 5
3 4
输出
5

【补充说明】数据中不会出现环，满足生物学的要求。（感谢 @AKEE ）

代码及分析如下：

`#include<bits/stdc++.h>
#include<algorithm>
#include<iostream>
#include<cstring>
#include<cstdlib>
#include<cstdio>
#include<vector>
#include<cmath>
#include<queue>
#include<deque>
#include<stack>
#include<set>
#include<map>
using namespace std;
int read(){int X=0,w=0;char ch=0;while(!isdigit(ch)){w|=ch=='-';ch=getchar();}while(isdigit(ch)){X=(X<<3)+(X<<1)+(ch^48);ch=getchar();}return w?-X:X;
}
char F[200];
void write(int x){if(x==0){putchar('0');return;}int cnt=0,tmp=x>0?x:-x;if(x<0){putchar( '-' );}while(tmp>0){F[cnt++]=tmp%10+'0';tmp/=10;}while(cnt>0){putchar(F[--cnt]);}
}
int n,m,ans;
const int mod=80112002;
const int N=0x3f3f3f;
queue<int> q;//拓扑排序模板所需队列； 
vector<int> p[N];//存每条有向边的起点和重点； 
int in[N],out[N],num[N];//每个点的入度和出度和伪食物链的个数； 
int main()
{n=read(),m=read();for(int i=1;i<=m;i++){int x=read(),y=read();in[y]++;//右端点入度+1;out[x]++;//左端点出度+1;p[x].push_back(y);//将这条有向边存起来;}for(int i=1;i<=n;i++){//寻找入度为零的点(源头生产者);if(in[i]==0){num[i]=1;//初始化;q.push(i);//加到队列当中；}}while(q.empty()==0){int sum=q.front();q.pop();int len=p[sum].size();for(int i=0;i<len;i++){//枚举以该点为起点的所有线段的终点;int now=p[sum][i];//取出目前枚举到的点;in[now]--;//将这个点的入度-1(因为目前要删除第tot个点)； num[now]=(num[now]+num[sum])%mod;//更新到下一个点的路径数量； if(in[now]==0){q.push(now);//如果这个点的入度为零了,那么加入队列； }}}for(int i=1;i<=n;i++){//寻找出度为0的点(尽头消费者);if(out[i]==0){ans=(ans+num[i])%mod;}}write(ans);return 0;
}`