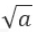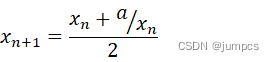一个实例

//java实现的sqrt类和方法
public class sqrt {public static double sqrt(double n){if (n<0) return Double.NaN;double err = 1e-15;double t = n;while (Math.abs(t - n/t) > err*t)t = (n/t + t)/2;return t;}public static void main(String[] args){sqrt a  = new sqrt();System.out.println(a.sqrt(2));}
}
//2的平方根的求解结果
>>1.414213562373095

迭代简介

迭代，是一种数值方法，具体指从一个初始值，一步步地通过迭代过程，逐步逼近真实值的方法。
与之相对的是直接法，也就是通过构建解析解，一步求出问题的方法。

通常情况下，我们总是喜欢一步得到问题的结果，因此直接法总是优先考虑的。
但是，当遇到复杂的问题时，特别在未知量很多，方程非线性时，无法得到直接解法（例如五次方程并没有解析解）。
这时候，我们需要使用迭代算法，一步步逼近，得到问题的答案。

迭代算法，通常需要考虑如下问题：
- 确定迭代变量
- 确定迭代关系式
- 确定迭代终止条件

牛顿迭代法

牛顿迭代法简介

牛顿迭代法，求解如下问题的根$x$

$$f(x) = 0$$

求解方法如下：

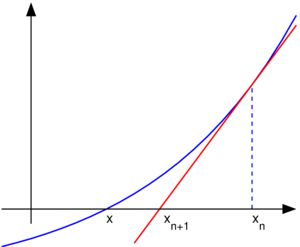
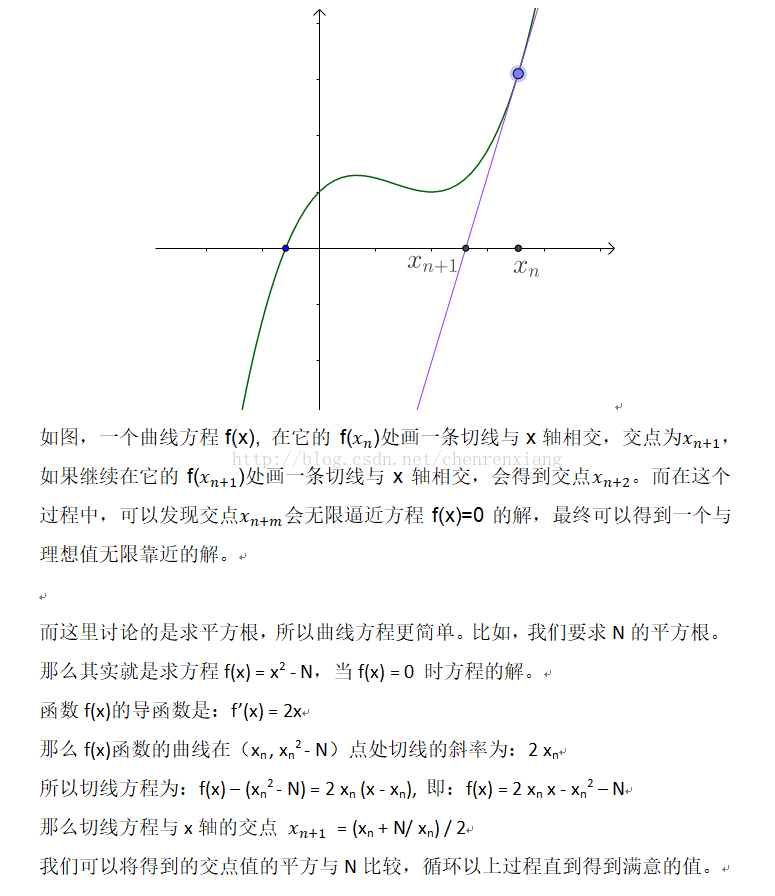
$$x_{n+1} = x_n - \frac{f(x_n)}{f'(x_n)}$$

方法中，迭代变量是根$x$，迭代关系式如上，迭代终止条件是$\vert f(x_n)-0 \vert <error$。

牛顿迭代法需要满足的条件是：
$f'(x)$是连续的，并且待求的零点$x$是孤立的。
那么，在零点$x$周围存在一个区域，只要初始值$x_0$位于这个邻域内，那么牛顿法必然收敛。
并且，如果$f'(x)$不为0，那么牛顿法将具有平方收敛的特性，也就是，每迭代一次，其结果的有效倍数将增加一倍。

简单推导

由

$$f'(x_n) = \frac{dy}{dx} = \frac{f(x_n)}{x_n - x_{n+1}}$$

有

$$x_{n+1} = x_n -\frac{f(x_n)}{f'(x_n)}$$

对于平方根问题，假设$f(x) = x^2 -n$，代入上式，有

$$x_{n+1} = \frac{1}{2} (x_n + \frac{n}{x_n})$$

其图像含义是：通过对接近零点的领域点做切线，不断逼近零点，最终十分靠近零点。

泰勒公式推导

上面的式子，同样，可以用泰勒公式推导出来。

$$f(x_n + \epsilon) = f(x_n) + f'(x_n)\epsilon + \frac{1}{2}f''(x)\epsilon^2+...$$
只取等号右边的前两项，有
$$\epsilon = \frac{f(x_n+\epsilon)-f(x_n)}{f'(x_n)}$$
两边同时加上 $x_n$，有
$$x_{n+1} = x_n + \epsilon = x_n +\frac{f(x_n+\epsilon)-f(x_n)}{f'(x_n)}=x_n +\frac{f(x_{n+1})-f(x_n)}{f'(x_n)}$$
最终， $f(x_{n+1}=0)$，假设 $f(x) = x^2 -n$，上式同样可以化成
$$x_{n+1} = \frac{1}{2} (x_n + \frac{n}{x_n})$$

本质上，牛顿迭代法就是利用了泰勒公式的前两项和，是泰勒公式的简化。

延伸与应用

同样的，牛顿迭代法同样可以求n次方根，对于$f(x)=x^m - n$
有

$$x_{n+1}=x_n-\frac{x_n}{m}(1-a{x_n}^{-m})$$