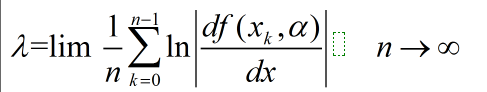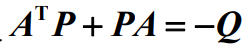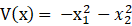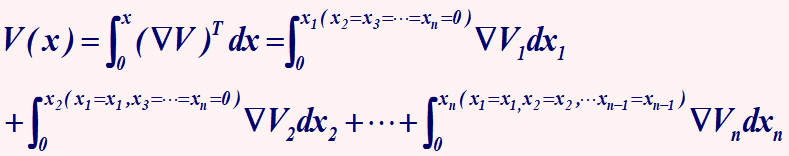简介

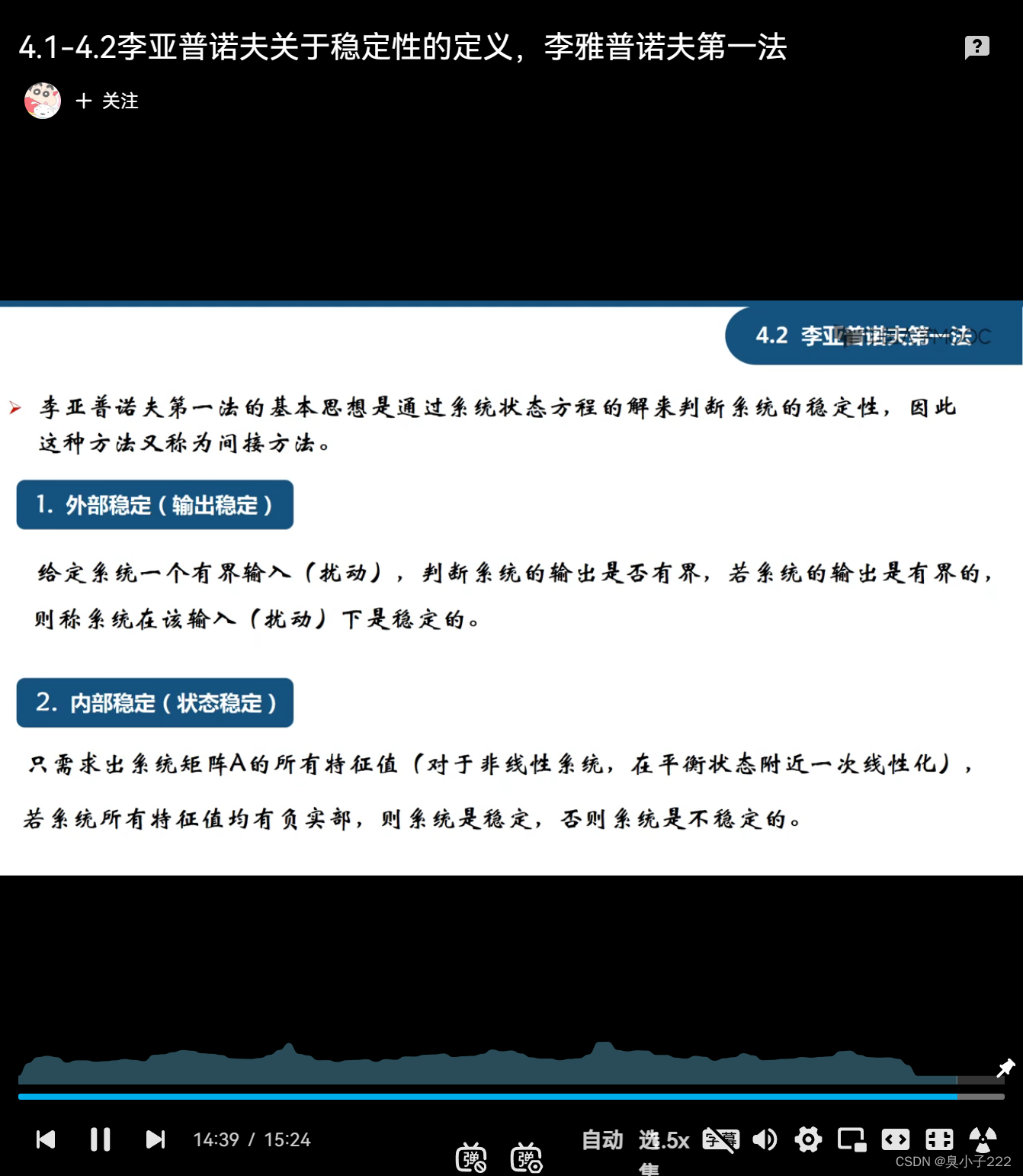
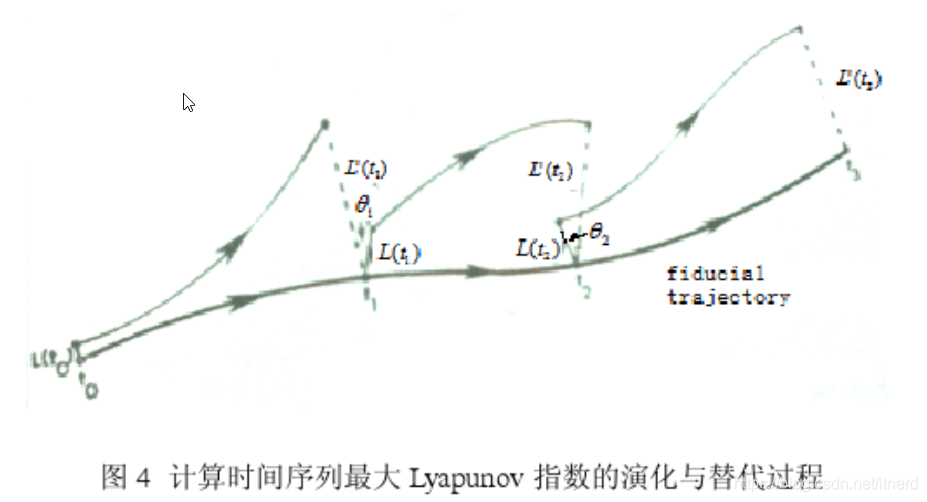
     李雅普诺夫指数是衡量混沌系统的一个重要参数，下面截图是对其具体解释。

代码实现：

clc;
clear; global kk;e=0ina1=0;final2=10;for kk=ina1:1:final2kk
InitialTime=0;	%Initial time
FinalTime=500;	%Final time
TimeStep=0.1;		%Time step
RelTol=1e-5;		%Relative tolerance
AbsTol=1e-6;		%Absolute toleranceDiscardItr=150;	%Iterations to be discarded
UpdateStepNum=10;	%Lyapunov exponents updating steps
linODEnum=9;	%No. of linearized ODEs
ic=[1 1 1];	%Initial conditions%Dimension of the linearized system (total: d x d ODEs)
d=sqrt(linODEnum);
%Initial conditions for the linearized ODEs
Q0=eye(d);
IC=[ic(:);Q0(:)];
ICnum=length(IC);		%Total no. of initial coniditions
%One iteration: Duration for updating the LEs
Iteration=UpdateStepNum*TimeStep;	
DiscardTime=DiscardItr*Iteration+InitialTime;T1=InitialTime;
T2=T1+Iteration;
TSpan=[T1:TimeStep:T2];
%Absolute tolerance of each components is set to the same value
options=odeset('RelTol',RelTol,'AbsTol',ones(1,ICnum)*AbsTol);%Initialize variables
n=0;		%Iteration counter
k=0;		%Effective iteration counter% (discarded iterations are not counted)
Sum=zeros(1,d);
xData=[];
yData=[];A=[];%Main loop
while (1)n=n+1;%Integration[t,X]=ode45('lyaphychaossf',TSpan,IC,options);    [rX,cX]=size(X);L=cX-linODEnum;      %No. of initial conditions for %the original systemfor i=1:dm1=L+1+(i-1)*d;m2=m1+d-1;A(:,i)=(X(rX,m1:m2))';end%QR decompositionif d>1%The algorithm for 1st-order system doesn't require%QR decomposition[Q,R]=qr(A);if T2>DiscardTimeQ0=Q;elseQ0=eye(d);endelseR=A;end%in the following calculation, so discard this step.permission=1;for i=1:dif R(i,i)==0permission=0;break;endend%To determine the Lyapunov exponentsif (T2>DiscardTime & permission)k=k+1;T=k*Iteration;TT=n*Iteration+InitialTime;%There are d Lyapunov exponentsSum=Sum+log(abs(diag(R))');Lambda=Sum/T;%Display the calculated Lyapunov exponents every 10 stepsif rem(k,10)==0Lambda  % Lambda is the calculated Lyapunov exponentsT2	 %Current timexData=[xData;TT]; %store the data to plotyData=[yData;Lambda];endend%If calculation is finished , exit the loop.if (T2>=FinalTime)%Show the final results (for making sure the final results being shown if DisplayStep>1)if (T2>DiscardTime & permission)Lambda
%         LD      %the Lyapunov dimensionendbreak;end%Update the initial conditions and time span for the next iterationic=X(rX,1:L);T1=T1+Iteration;T2=T2+Iteration;TSpan=[T1:TimeStep:T2];IC=[ic(:);Q0(:)];
end		%End of main loop
pp=length(yData(:,1));
e=e+1;
ll(e,1)= yData(pp,1);
ll(e,2)= yData(pp,2);
ll(e,3)= yData(pp,3);
%ll(e,4)= yData(pp,4);
endbb=ina1:1:final2;
plot(bb, ll(:,1),bb, ll(:,2),bb, ll(:,3));grid;

 [t,X]=ode45('lyaphychaossf',TSpan,IC,options);    %词句调用的'lyaphychaossf'为一份.m文件，文件内容为chen系统的方程转换的雅克比行列式。

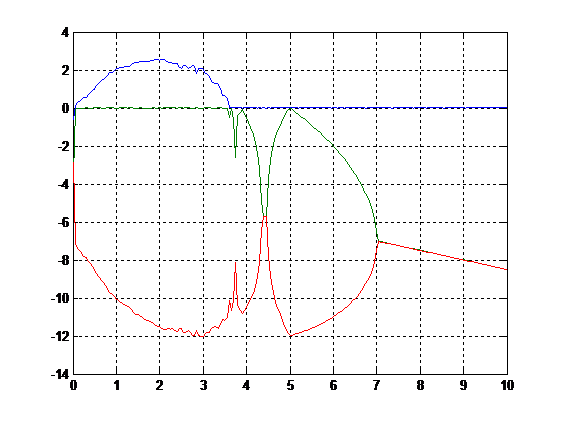
结果如下图：

可看出，此仿真程序仿真出的图示与理论分析结果一致。