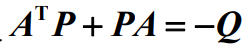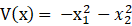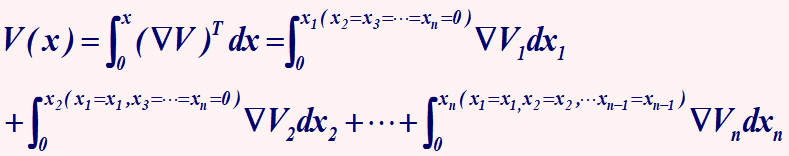李雅普诺夫稳定性

在数学和自动控制领域中，李雅普诺夫稳定性（英语：Lyapunov stability，或李亚普诺夫稳定性）可用来描述一个动力系统的稳定性。如果此动力系统任何初始条件在 {\displaystyle x_{0}} $86f21d0e31751534cd6584264ecf864a6aa792cf$ 转存失败重新上传取消 $x_{0}$ 附近的轨迹均能维持在 {\displaystyle x_{0}} $86f21d0e31751534cd6584264ecf864a6aa792cf$ 转存失败重新上传取消 $x_{0}$ 附近，那么该系统可以称为在{\displaystyle x_{0}} $86f21d0e31751534cd6584264ecf864a6aa792cf$ 转存失败重新上传取消 $x_{0}$ 处李雅普诺夫稳定。

若任何初始条件在 {\displaystyle x_{0}} $86f21d0e31751534cd6584264ecf864a6aa792cf$ 转存失败重新上传取消 $x_{0}$ 附近的轨迹最后都趋近{\displaystyle x_{0}} $86f21d0e31751534cd6584264ecf864a6aa792cf$ 转存失败重新上传取消 $x_{0}$ ，那么该系统可以称为在{\displaystyle x_{0}} $86f21d0e31751534cd6584264ecf864a6aa792cf$ 转存失败重新上传取消 $x_{0}$ 处渐近稳定。指数稳定可用来保证系统最小的衰减速率，也可以估计轨迹收敛的快慢。[1]

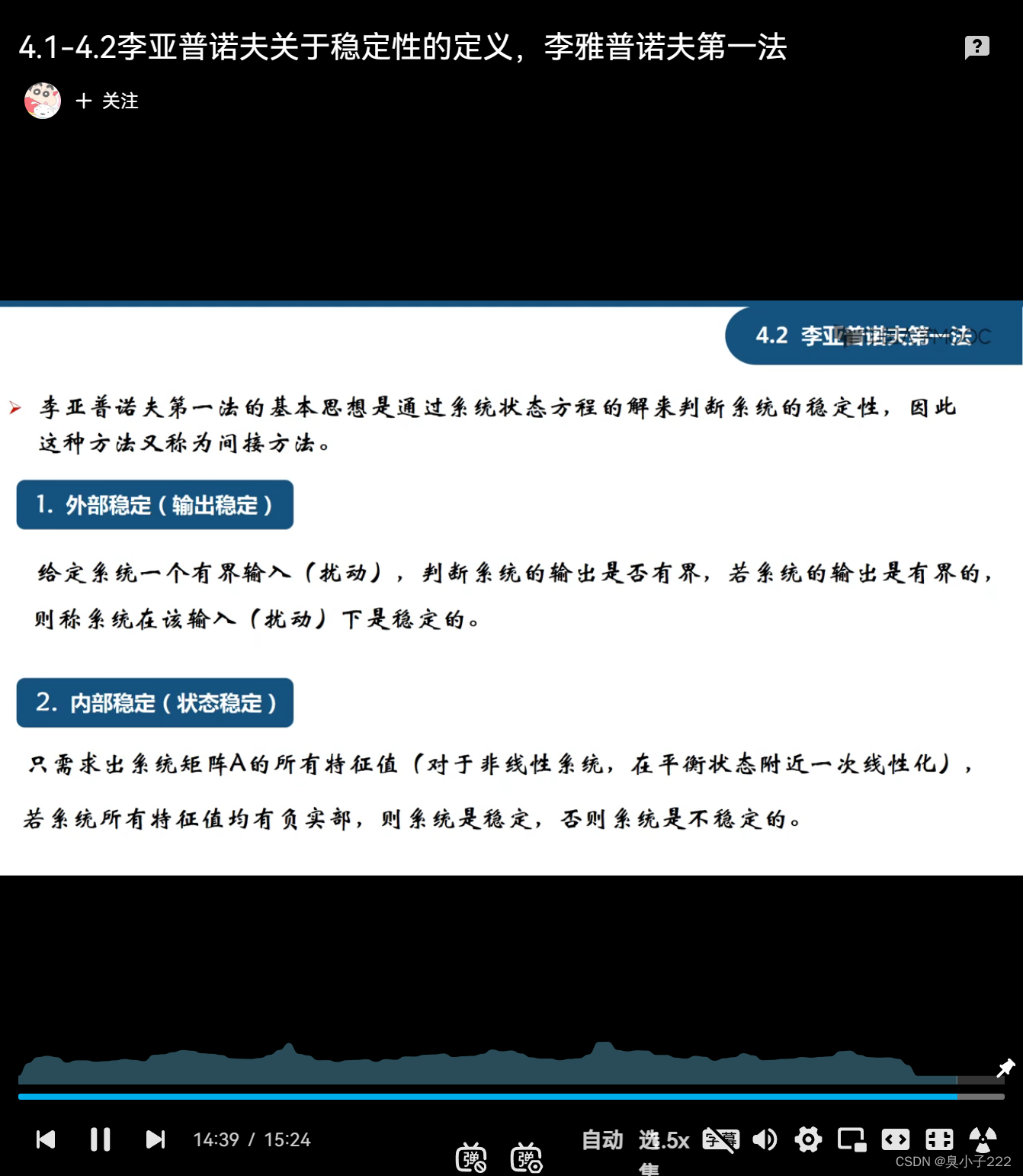
李雅普诺夫稳定性可用在线性及非线性的系统中。不过线性系统的稳定性可由其他方式求得，因此李雅普诺夫稳定性多半用来分析非线性系统的稳定性。李亚普诺夫稳定性的概念可以延伸到无限维的流形，即为结构稳定性，是考虑微分方程中一群不同但“接近”的解的行为。输入-状态稳定性（ISS）则是将李雅普诺夫稳定性应用在有输入的系统。

历史[编辑]

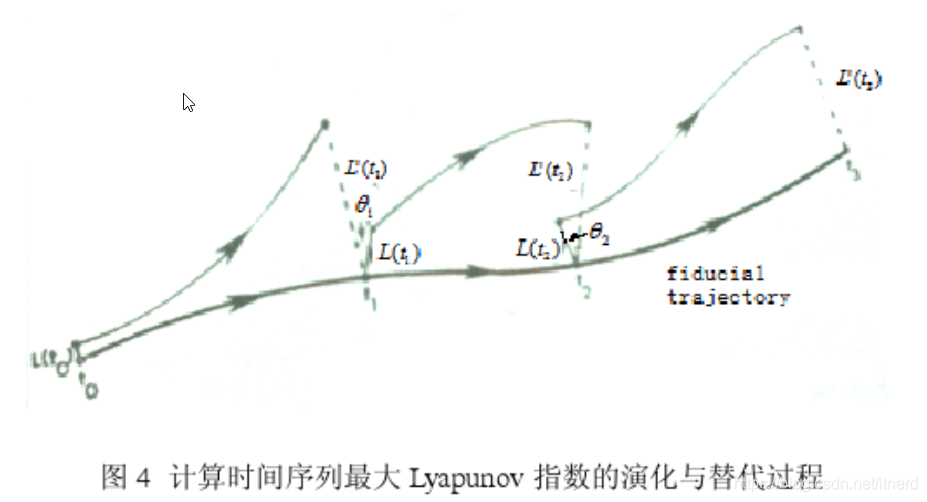
这一稳定性以俄国数学家亚历山大·李亚普诺夫命名，他在1892年发表了他的博士论文《运动稳定性的一般问题》，文中给出了稳定性的科学概念、研究方法和相关理论。李雅普诺夫考虑到针对非线性系统修改稳定理论，修正为以一个稳定点线性化的系统为基础的线性稳定理论。他的作品最初以俄文发行，后翻译为法文，但多年来默默无闻。人们对它的兴趣突然在冷战初期（1953至1962年）开始，因当所谓的“李雅普诺夫第二方法”被认为适用于航空航天制导系统的稳定性，而这系统通常包含很强的非线性，其他方法并不适用。大量的相关出版物自那时起开始出现，并进入控制系统文献中。最近李雅普诺夫指数的概念（与李雅普诺夫稳定性第一种方法）引起了广泛兴趣，并与混沌理论结合了起来。

连续时间系统下的定义[编辑]

给定一个完备的赋范向量空间E（例如{\displaystyle \mathbb {R} ^{n}} $c510b63578322050121fe966f2e5770bea43308d$ 转存失败重新上传取消 $\mathbb {R} ^{n}$ ），设U是E的开子集。考虑一个自治的非线性动力系统：

{\displaystyle {\dot {x}}=f(x(t)),\;\;\;\;x(t_{0})=x_{0}} $178b5ff2069f3bf370f215e967db54a13c605f60$ 转存失败重新上传取消 ${\dot {x}}=f(x(t)),\;\;\;\;x(t_{0})=x_{0}$ ,

其中{\displaystyle x(t)\in U} $4a1801eca94d66e13247ada17a941d079a183234$ 转存失败重新上传取消 $x(t)\in U$ 是系统的状态向量，{\displaystyle f:U\rightarrow E} $b35428af747bddb18af36bdcbdebbc7f0c6f6841$ 转存失败重新上传取消 $f:U\rightarrow E$ 是U上的连续函数。

假设函数f有一个零点：f(a) = 0，则常数函数：x = a是动力系统的驻定解（或称平衡解）。称a是动力系统的平衡点。

称点a李雅普诺夫稳定（简称稳定），如果对每个{\displaystyle \epsilon >0} $568095ad3924314374a5ab68fae17343661f2a71$ 转存失败重新上传取消 $\epsilon >0$ ，均存在{\displaystyle \delta =\delta (\epsilon )>0} $cff71046f7732a232f7fcefe6b236c5838c1e650$ 转存失败重新上传取消 $\delta =\delta (\epsilon )>0$ ，使得对所有满足{\displaystyle \|x_{0}-a\|<\delta } $f73024b4117bd935c4618614da312ab2587f51c0$ 转存失败重新上传取消 $\|x_{0}-a\|<\delta$ 的{\displaystyle x_{0}} $86f21d0e31751534cd6584264ecf864a6aa792cf$ 转存失败重新上传取消 $x_{0}$ ，只要{\displaystyle t\geqslant t_{0}} $beaa76a0ce79c74a5377dd2a034260b8d24ee518$ 转存失败重新上传取消 $t\geqslant t_{0}$ ，就有{\displaystyle \|x(t)-a\|<\epsilon } $d07d6219d37f8318ac86da220d8860078c891888$ 转存失败重新上传取消 $\|x(t)-a\|<\epsilon$ 。
称点a渐近稳定，如果点a李雅普诺夫稳定，且存在{\displaystyle \delta >0} $595d5cea06fdcaf2642caf549eda2cfc537958a9$ 转存失败重新上传取消 $\delta >0$ ，使得对所有满足 {\displaystyle \|x_{0}-a\|<\delta } $f73024b4117bd935c4618614da312ab2587f51c0$ 转存失败重新上传取消 $\|x_{0}-a\|<\delta$ 的{\displaystyle x_{0}} $86f21d0e31751534cd6584264ecf864a6aa792cf$ 转存失败重新上传取消 $x_{0}$ ，{\displaystyle \lim _{t\rightarrow \infty }x(t)=a} $550de3e8b93a59397066163f0e03d793392b0bbd$ 转存失败重新上传取消 $\lim _{{t\rightarrow \infty }}x(t)=a$ 。
称点a指数稳定，如果点a渐近稳定，且存在 {\displaystyle \alpha ,\beta ,\delta >0} $07a3ff6b2899a5d6f9e4af535218739a841655f1$ 转存失败重新上传取消 $\alpha ,\beta ,\delta >0$ 使得对所有满足{\displaystyle \|x_{0}-a\|<\delta } $f73024b4117bd935c4618614da312ab2587f51c0$ 转存失败重新上传取消 $\|x_{0}-a\|<\delta$ 的{\displaystyle x_{0}} $86f21d0e31751534cd6584264ecf864a6aa792cf$ 转存失败重新上传取消 $x_{0}$ ，只要{\displaystyle t\geqslant t_{0}} $beaa76a0ce79c74a5377dd2a034260b8d24ee518$ 转存失败重新上传取消 $t\geqslant t_{0}$ ，就有{\displaystyle \|x(t)-a\|\leq \alpha \|x_{0}-a\|e^{-\beta t}} $911987543c5c06a5c8a085a02e1776874b4762b4$ 转存失败重新上传取消 $\|x(t)-a\|\leq \alpha \|x_{0}-a\|e^{{-\beta t}}$ 。

它们的直观几何意义是：

平衡点为李雅普诺夫稳定的，表示若动力系统状态函数（微分方程的解函数）的初值“足够接近”平衡点，则它会永远维持在平衡点附近任意小的范围里（距平衡点的距离不超过任意选择的正实数 {\displaystyle \epsilon } $c3837cad72483d97bcdde49c85d3b7b859fb3fd2$ 转存失败重新上传取消 $\epsilon$ ）。
渐近稳定的意思是，初值足够接近平衡点的状态函数，不但维持在平衡点附近，而且最后会收敛到平衡点。
指数稳定的意思是，状态函数不但最后会收敛到平衡点，且收敛速度不慢于某种指数递减的速度。

设有状态函数x，其初始取值为{\displaystyle x(t_{0})=x_{0}} $aabccfdf83c824bd305a2b9d7554bfc7d30e4763$ 转存失败重新上传取消 $x(t_{0})=x_{0}$ 。称{\displaystyle {\bar {x}}=\{x(t);\;t\geqslant t_{0}\}} $f7ca946946b4ca2b5cc2a6bdc33f3bfd65f1e3ea$ 转存失败重新上传取消 ${\bar {x}}=\{x(t);\;t\geqslant t_{0}\}$ 为x的轨迹。如果对所有初始值与x足够接近的状态函数y，两者的轨迹会趋于相同：

{\displaystyle \lim _{t\to \infty }\|y(t)-x(t)\|\longrightarrow 0.} $3f9c4bcc4ce34744d9104897fa705f59dc1aff2d$ 转存失败重新上传取消 $\lim _{{t\to \infty }}\|y(t)-x(t)\|\longrightarrow 0.$

则称x的轨迹有（局部）吸引性（attractive）。若上述条件对所有y均成立，则称x有全局吸引性（globally attractive）。

如果x的轨迹有吸引性，并且稳定，则x渐近稳定。不过，x有吸引性不表示它的轨迹渐近稳定。

迭代系统下的定义[编辑]

离散时间系统下稳定性的定义和连续时间系统下的定义几乎相同。以下为其定义，不过使用的是较多数学书籍上使用的定义。

给定度量空间{\displaystyle (X,d)} $cb4d7a16bca9e216c0221b43a1c3377aa5e358b8$ 转存失败重新上传取消 $(X,d)$ 。设{\displaystyle f\colon X\to X} $773c98269d8a3c82725e5cb650243666484b528b$ 转存失败重新上传取消 $f\colon X\to X$ 为一连续函数。称点{\displaystyle a\in X} $f6201478b1190a333ea731849684429a697638dc$ 转存失败重新上传取消 $a\in X$ 为李雅普诺夫稳定，如果对任意{\displaystyle \epsilon >0} $568095ad3924314374a5ab68fae17343661f2a71$ 转存失败重新上传取消 $\epsilon >0$ ，都存在{\displaystyle \delta >0} $595d5cea06fdcaf2642caf549eda2cfc537958a9$ 转存失败重新上传取消 $\delta >0$ ，使得只要{\displaystyle x\in X} $3e580967f68f36743e894aa7944f032dda6ea01d$ 转存失败重新上传取消 $x \in X$ 满足{\displaystyle d(x,a)<\delta } $87560695b82ae88d6f524e6c500173085db69795$ 转存失败重新上传取消 $d(x,a)<\delta$ ，就有

{\displaystyle \forall n\in \mathbb {N} ,\;\;d(f^{n}(x),f^{n}(a))<\epsilon .} $0f06726c33a84efb4d3f88b08bdea0ce00fb353f$ 转存失败重新上传取消 $\forall n\in {\mathbb {N}},\;\;d(f^{n}(x),f^{n}(a))<\epsilon .$

称点a渐近稳定，如果a是李雅普诺夫稳定的点，而且在稳定点集合的内部，即存在{\displaystyle \delta >0} $595d5cea06fdcaf2642caf549eda2cfc537958a9$ 转存失败重新上传取消 $\delta >0$ ，使得只要{\displaystyle x\in X} $3e580967f68f36743e894aa7944f032dda6ea01d$ 转存失败重新上传取消 $x \in X$ 满足{\displaystyle d(x,a)<\delta } $87560695b82ae88d6f524e6c500173085db69795$ 转存失败重新上传取消 $d(x,a)<\delta$ ，就有

{\displaystyle \lim _{n\to \infty }d(f^{n}(x),f^{n}(a))=0} $9cd792e2b9b20be0368a4f221fbcc9a139563010$ 转存失败重新上传取消 $\lim _{{n\to \infty }}d(f^{n}(x),f^{n}(a))=0$

李雅普诺夫稳定性理论[编辑]

对于微分方程解之稳定性的研究称为稳定性理论。而李雅普诺夫稳定性定理只提供了稳定性的充份条件。

李雅普诺夫稳定性第二定理[编辑]

考虑一个函数 V(x) : Rn → R 使得

{\displaystyle V(x)\geq 0} $7aaf7d9324436b55831d7469bd55dbbb6bf2dce1$ 转存失败重新上传取消 $V(x)\geq 0$ 只有在 {\displaystyle x=0} $953917eaf52f2e1baad54c8c9e3d6f9bb3710cdc$ 转存失败重新上传取消 $x=0$ 处等号成立（正定函数）
{\displaystyle {\dot {V}}(x(t))<0} $4429b9af4a834b8b12e562791bf832d266c9d5c1$ 转存失败重新上传取消 ${\dot {V}}(x(t))<0$ （负定）

则V(x)称为李雅普诺夫候选函数（Lyapunov function candidate），且系统（依李雅普诺夫的观点）为渐近稳定。

上式中 {\displaystyle V(0)=0} $0ffc80c79788cb45deb8877c217f57be8e1eedbd$ 转存失败重新上传取消 $V(0)=0$ 是必要的条件。否则，{\displaystyle V(x)=1/(1+|x|)} $8393dd949fc4686868522b8d5a0276680589f5e0$ 转存失败重新上传取消 $V(x)=1/(1+|x|)$ 可以用来“证明” {\displaystyle {\dot {x}}(t)=x} $dc4f34667baed402f3c7bf493acdf0d369c04cfe$ 转存失败重新上传取消 ${\dot x}(t)=x$ 有区域性稳定。另一个称为径向无界性（radial unboundedness）的条件则是用来得到全域渐近稳定的结果。

此种分析方式可类比为考虑一物理系统（如弹簧及质量的系统）及其中的能量。若系统能量随时间递减，且减少的能量不会恢复，而此系统最后一定会静止于某个特定的状态。最后的状态称为吸引子。不过针对一个物理系统，找到表达其精确能量的函数不一定容易，而且针对抽象数学系统、经济系统或生物系统，上述能量的概念又不一定适用。

利用李雅普诺夫的分析方式，可在不知道系统实际能量的情形下，证明系统的稳定性。不过前提是可以找到满足上述限制的李雅普诺夫函数。

例如考虑以下的系统

{\displaystyle {\dot {x}}=-x^{3}\,} $a0325fa0a43c2b9122182da04b640a5e2c7cad8e$ 转存失败重新上传取消 ${\dot {x}}=-x^{3}\,$

希望用李雅普诺夫函数来确认{\displaystyle x=0\,} $41dfd404b94b20856e246e74091140d601931838$ 转存失败重新上传取消 $x=0\,$ 附近的稳定性。令

{\displaystyle V(x)=0.5x^{2}\,} $21b14d2a9fa16a25a383d1f00c7face6e98bad08$ 转存失败重新上传取消 $V(x)=0.5x^{2}\,$

{\displaystyle V(x)} $4ab3e825c2bf9c80d11d12e070a4626d48e03c61$ 转存失败重新上传取消 $V(x)$ 本身为正定函数．而V(x)的导函数如下

{\displaystyle {\dot {V}}(x(t))={\partial V \over \partial x}(-x^{3})=-x^{4}\,} $1fc6be04b2ca1f0d681c0be9ab3e3bac48a66b71$ 转存失败重新上传取消 ${\dot {V}}(x(t))={\partial V \over \partial x}(-x^{3})=-x^{4}\,$

为负定函数，因此上述系统在{\displaystyle x=0\,} $41dfd404b94b20856e246e74091140d601931838$ 转存失败重新上传取消 $x=0\,$ 附近为渐近稳定。

线性系统状态空间模型的稳定性[编辑]

一个线性的状态空间模型

{\displaystyle {\dot {\textbf {x}}}=A{\textbf {x}}} $a6c812ec4d414ceadba420c3f18ab31a32d03192$ 转存失败重新上传取消 ${\dot {{\textbf {x}}}}=A{\textbf {x}}$

为渐近稳定（其实是指数稳定），若

{\displaystyle A^{T}M+MA+N=0} $16928707f668ae21b8b424307fe6cb7712873f3c$ 转存失败重新上传取消 $A^{{T}}M+MA+N=0$

的解存在。

其中 {\displaystyle N=N^{T}>0} $9ed17273c937c4b3c625024a5ff453a29805afa6$ 转存失败重新上传取消 $N=N^{{T}}>0$ 且 {\displaystyle M=M^{T}>0} $d9e5be76ddb960db13f20f83e010fc16e14fdec0$ 转存失败重新上传取消 $M=M^{{T}}>0$ （正定矩阵）。（对应的李雅普诺夫函数为{\displaystyle V(x)=x^{T}Mx} $5b7964693981d1a98a8bbc3cbeea87b8d97eb10a$ 转存失败重新上传取消 $V(x)=x^{T}Mx$ ）

有输入值系统的稳定性[编辑]

一个有输入（或受控制）的系统可以下式表示

{\displaystyle {\dot {\textbf {x}}}={\textbf {f(x,u)}}} $2391f7c32f7fbe8559c9a833b96f6810f9a33b02$ 转存失败重新上传取消 ${\dot {{\textbf {x}}}}={\textbf {f(x,u)}}$