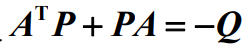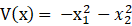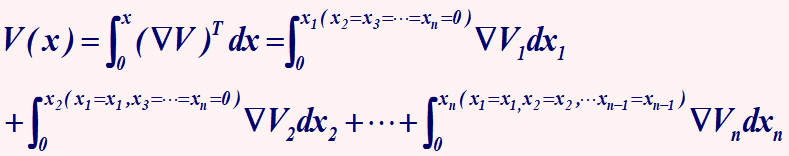
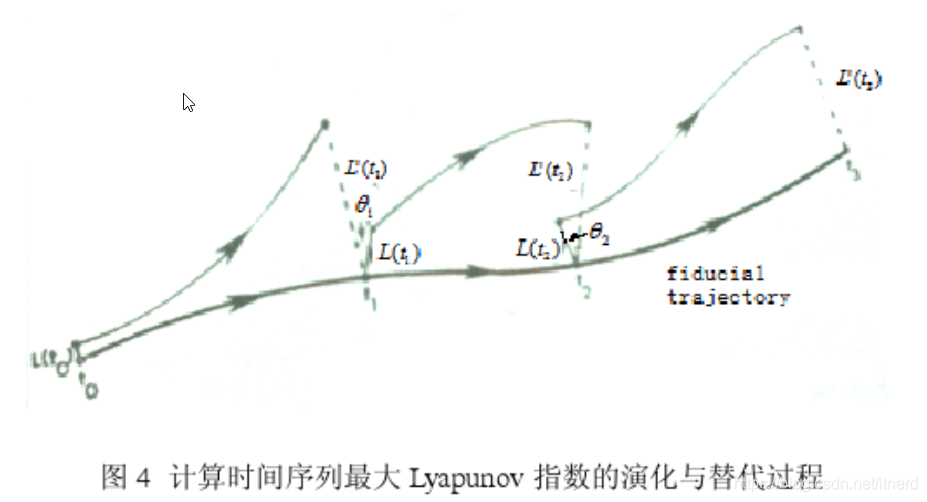
参考原理:
Lyapunov 指数的计算与仿真:https://wenku.baidu.com/view/ae8e4f80680203d8ce2f2476.html
Lorenz 系统的动力学方程
function dX = Lorenz(t,X,params) a = params(1);
b = params(2);
c = params(3);x=X(1);
y=X(2);
z=X(3);dX = zeros(3,1);
dX(1)=a*(y-x);
dX(2)=x*(b-z)-y;
dX(3)=x*y-c*z;end
使用 G. Benettin 计算方法
Z=[];
a=10;
c=8/3;
d0=1e-7;
bs = linspace(0,300,301);
transient = 50;
for b=bsparams = [a,b,c];lsum=0; x=1;y=1;z=1; % #初始基准点x1=1;y1=1;z1=1+d0; % #初始偏离点for i=1:100 [T1,Y1]=ode45(@(t,X) Lorenz(t,X,params),[0 1],[x;y;z]); [T2,Y2]=ode45(@(t,X) Lorenz(t,X,params),[0 1],[x1;y1;z1]); n1=length(Y1);n2=length(Y2); x=Y1(n1,1);y=Y1(n1,2);z=Y1(n1,3); x1=Y2(n2,1);y1=Y2(n2,2);z1=Y2(n2,3); d1=sqrt((x-x1)^2+(y-y1)^2+(z-z1)^2); % #新的偏离点在上一次计算的两轨迹末端的连线上,且距离仍等于d0x1=x+(d0/d1)*(x1-x); y1=y+(d0/d1)*(y1-y); z1=z+(d0/d1)*(z1-z); % #舍弃暂态过程的数据,因为初始基准点不一定在吸引子上if i> transientlsum=lsum+log(d1/d0); end end Z=[Z lsum/(i-transient)];
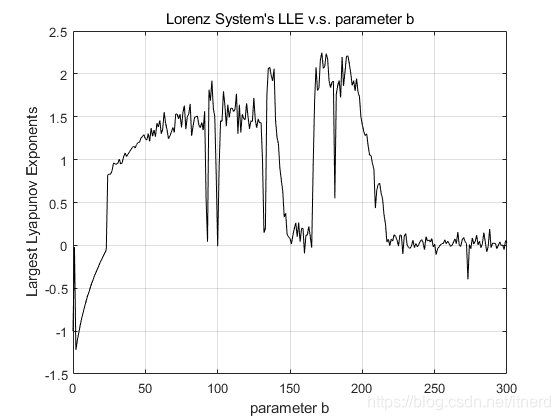
end plot(bs,Z,'-k');
title('Lorenz System''s LLE v.s. parameter b')
xlabel('parameter b'),ylabel('Largest Lyapunov Exponents');
grid on;
代码二
clear;
yinit = [0.1,0.1,0.1];
orthmatrix = [1 0 0;0 1 0;0 0 1];y = zeros(12,1);
% 初始化输入
y(1:3) = yinit;
y(4:12) = orthmatrix;
tstart = 0; % 时间初始值
tstep = 1e-3; % 时间步长
wholetimes = 1e5; % 总的循环次数
steps = 10; % 每次演化的步数
iteratetimes = wholetimes/steps; % 演化的次数
mod = zeros(3,1);
lp = zeros(3,1);
% 初始化三个Lyapunov指数
Lyapunov1 = zeros(iteratetimes,1);
Lyapunov2 = zeros(iteratetimes,1);
Lyapunov3 = zeros(iteratetimes,1);
for i=1:iteratetimestspan = tstart:tstep:(tstart + tstep*steps); [T,Y] = ode45(@(t,y) Lorenz_ly(t,y), tspan, y);% 取积分得到的最后一个时刻的值y = Y(size(Y,1),:);% 重新定义起始时刻tstart = tstart + tstep*steps;y0 = [y(4) y(7) y(10);y(5) y(8) y(11);y(6) y(9) y(12)];%正交化y0 = ThreeGS(y0);% 取三个向量的模mod(1) = sqrt(y0(:,1)'*y0(:,1));mod(2) = sqrt(y0(:,2)'*y0(:,2));mod(3) = sqrt(y0(:,3)'*y0(:,3));y0(:,1) = y0(:,1)/mod(1);y0(:,2) = y0(:,2)/mod(2);y0(:,3) = y0(:,3)/mod(3);lp = lp+log(abs(mod));%三个Lyapunov指数Lyapunov1(i) = lp(1)/(tstart);Lyapunov2(i) = lp(2)/(tstart);Lyapunov3(i) = lp(3)/(tstart);y(4:12) = y0';
end
% 作Lyapunov指数谱图
figure,
i = 1:iteratetimes;
plot(i,Lyapunov1,i,Lyapunov2,i,Lyapunov3)%G-S正交化
function A = ThreeGS(V) % V 为3*3向量
v1 = V(:,1);
v2 = V(:,2);
v3 = V(:,3);
a1 = zeros(3,1);
a2 = zeros(3,1);
a3 = zeros(3,1);
a1 = v1;
a2 = v2-((a1'*v2)/(a1'*a1))*a1;
a3 = v3-((a1'*v3)/(a1'*a1))*a1-((a2'*v3)/(a2'*a2))*a2;
A = [a1,a2,a3];
endfunction dX = Rossler_ly(t,X)
% Rossler吸引子,用来计算Lyapunov指数
% a=0.15,b=0.20,c=10.0
% dx/dt = -y-z,
% dy/dt = x+ay,
% dz/dt = b+z(x-c),
a = 0.20;
b = 0.20;
c = 5.7;
x=X(1); y=X(2); z=X(3);
% Y的三个列向量为相互正交的单位向量
Y = [X(4), X(7), X(10);X(5), X(8), X(11);X(6), X(9), X(12)];
% 输出向量的初始化,必不可少
dX = zeros(12,1);
% Rossler吸引子
dX(1) = -y-z;
dX(2) = x+a*y;
dX(3) = b+z*(x-c);
% Rossler吸引子的Jacobi矩阵
Jaco = [0 -1 -1;1 a 0;z 0 x-c];
dX(4:12) = Jaco*Y;
endfunction dX = Lorenz_ly(t,X)
% Lorenz 吸引子,用来计算Lyapunov指数
a = 10;
b = 28;
c = 8/3;
x=X(1); y=X(2); z=X(3);
% Y的三个列向量为相互正交的单位向量
Y = [X(4), X(7), X(10);X(5), X(8), X(11);X(6), X(9), X(12)];
% 输出向量的初始化,必不可少
dX = zeros(12,1);
% Lorenz 吸引子
dX(1)=a*(y-x);
dX(2)=x*(b-z)-y;
dX(3)=x*y-c*z;
% Lorenz 吸引子的Jacobi矩阵
Jaco = [-a a 0;b-z -1 -x;y x -c];
dX(4:12) = Jaco*Y;
end