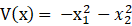0 背景和思路
**系统稳定:**系统储存的总能量持续地减小,直至耗尽,系统状态就会趋于平衡态
**稳定性考察:**考察一个正值的能量函数 V ( x ) V(\boldsymbol{x}) V(x) 和它的变化率 V ˙ ( x ) \dot{V}(\boldsymbol{x}) V˙(x) 来判断。若 V ˙ ( x ) \dot{V}(\boldsymbol{x}) V˙(x) 始终为负,则系统稳定。
**困难:**对于一般的动态系统,并不是总能明确地定义一个能量函数
**解决方案:**用一个正定的标量函数作为系统的广义能量函数
这个标量函数是什么:运用李雅普诺夫第二方法判断系统稳定性时,常常采用二次型的标量函数。所谓二次型函数,是指形如:
V ( x ) = x T P x V(\boldsymbol{x})=\boldsymbol{x}^TP\boldsymbol{x} V(x)=xTPx
这里P是实对称矩阵。设:
[ P 11 P 12 ⋯ P 1 n P 21 P 22 ⋯ P 2 n ⋮ ⋮ ⋮ P n 1 P n 2 ⋯ P n n ] \begin{bmatrix} P_{11}&P_{12}&\cdots&P_{1n}\\ P_{21}&P_{22}&\cdots&P_{2n}\\ \vdots&\vdots&&\vdots\\ P_{n1}&P_{n2}&\cdots&P_{nn} \end{bmatrix} ⎣⎢⎢⎢⎡P11P21⋮Pn1P12P22⋮Pn2⋯⋯⋯P1nP2n⋮Pnn⎦⎥⎥⎥⎤
则V的正定性可以用西尔维斯特(Sylvester) 准则来判断:
(1)二次型正定:即P矩阵正定:顺序主子式都大于0
(2)二次型(或P)负定:充要:P的主子式满足:
Δ 2 i − 1 < 0 , Δ 2 i > 0 , i = 1 , 2 , ⋯ \Delta_{2i-1}<0,\quad\Delta_{2i}>0,\quad i=1,2,\cdots Δ2i−1<0,Δ2i>0,i=1,2,⋯
注:
要求正定,则说明V是正值能量函数,要求二次型,则符合能量特征
1 李雅普诺夫第二方法
取非线性定常系统状态方程为:
x ˙ ( t ) = F ( x ( t ) ) \dot{\boldsymbol{x}}(t)=F(\boldsymbol{x}(t)) x˙(t)=F(x(t))
系统平衡状态:
x e = 0 \boldsymbol{x}_e=0 xe=0
定理1:
(寻找李雅普诺夫函数,使得系统渐近稳定)
- 对于具有连续一阶偏导数的标量函数 V ( x ) V(\boldsymbol{x}) V(x),如果 V ( x ) V(\boldsymbol{x}) V(x) 正定, V ( x ) V(\boldsymbol{x}) V(x) 的导数负定,则系统平衡状态是渐近稳定的,这样的 V ( x ) V(\boldsymbol{x}) V(x) 就是系统的一个李雅普诺夫函数。
- 如果在 1 成立的情况下, V ( x ) V(\boldsymbol{x}) V(x) 还满足径向无界条件:
lim ∣ ∣ ∣ x ∣ ∣ → ∞ V ( x ) = ∞ , w h e r e ∣ ∣ x ∣ ∣ = ∑ i = 1 n x i 2 \lim_{|||\boldsymbol{x}||\rightarrow\infty}V(\boldsymbol{x})=\infty, \; where \; ||\boldsymbol{x}||=\sqrt{\sum\limits_{i=1}^n\boldsymbol{x}_i^2} ∣∣∣x∣∣→∞limV(x)=∞,where∣∣x∣∣=i=1∑nxi2
那么平衡状态在整个状态空间中是大范围渐近稳定的。
问题:在定理1中,如果V的导数是半负定的,一般只能确定系统平衡状态在李雅普诺夫意义下是稳定的,但不能确定其渐近稳定性。
解决方案:加一个限制条件,见定理2。
定理2:
(没找到满足定理1的李雅普诺夫函数,但是找到了自身正定、导数半负定的V,也想实现渐近稳定性)
如果V在系统状态方程的任一非零解的状态运动轨迹上不恒为0,那么系统的平衡状态也是渐近稳定的(#跟减函数相似)。如果V径向无界,那么系统是大范围渐近稳定的。

定理3:
(判断系统的不稳定性)
如果找到了有连续一阶偏导数的标量函数V,满足V正定,V的导数也正定,那么系统平衡状态是不稳定的。
3 李雅普诺夫稳定性分析
对于只有唯一平衡状态的线性定常系统,平衡状态的大范围稳定性与系统的稳定性是一回事,因此就不加区分了。下面将分别介绍用李雅普诺夫第二方法(下称李二法)来分析线性定常连续时间系统和线性定常离散时间系统的稳定性。
(1)线性定常连续时间系统
状态方程:
x ˙ ( t ) = A x ( t ) \dot{\boldsymbol{x}}(t)=A\boldsymbol{x}(t) x˙(t)=Ax(t)
系统唯一平衡态:
x e = 0 \boldsymbol{x}_e=0 xe=0
李函数变化率:
V ˙ ( x ) = x T ˙ P x + x T P x ˙ = ( A x ) T P x + x T P A x = x T ( A T P + P A ) x \begin{aligned} \dot{V}(\boldsymbol{x})&=\dot{\boldsymbol{x}^T}P\boldsymbol{x}+\boldsymbol{x}^TP\dot{\boldsymbol{x}}\\ &=(A\boldsymbol{x})^TP\boldsymbol{x}+\boldsymbol{x}^TPA\boldsymbol{x}\\ &=\boldsymbol{x}^T(A^TP+PA)\boldsymbol{x} \end{aligned} V˙(x)=xT˙Px+xTPx˙=(Ax)TPx+xTPAx=xT(ATP+PA)x
记
Q = − ( A T P ) + P A Q=-(A^TP)+PA Q=−(ATP)+PA
为了使系统渐近稳定,Q应该正定。
问题:有时候P选得不好,Q既不是正定的也不是负定的,就不能用李二法判断系统稳定性了。
解决方案:实际用李二法的时候,一般先确定一个正定的Q,然后求解下面的李方程:
A T P + P A = − Q A^TP+PA=-Q ATP+PA=−Q
再找到正定的P。只要系统是渐近稳定的,那么这个李方程就一定存在正定解。也就是说,已知系统渐近稳定,那么一定存在李函数。这和前面用李函数判断渐近稳定性刚好反过来。这也就有了定理4。
定理4:
线性定常连续时间系统渐近稳定的充要条件:对任意给定的正定矩阵Q,存在正定矩阵P为李方程的解。
因为Q是任意的,所以一般来说,Q取单位阵,最简单了。
(2)线性定常离散时间系统
系统状态方程:
x ( k + 1 ) = A x ( k ) \boldsymbol{x}(k+1)=A\boldsymbol{x}(k) x(k+1)=Ax(k)
系统唯一平衡态:
x e = 0 \boldsymbol{x}_e=0 xe=0
李函数:
V ( x ) = x T P x V(\boldsymbol{x})=\boldsymbol{x}^TP\boldsymbol{x} V(x)=xTPx
因为是离散时间系统,所以用 V ( x ( k + 1 ) ) − V ( x ( k ) V(\boldsymbol{x}(k+1))-V(\boldsymbol{x}(k) V(x(k+1))−V(x(k) 作为变化率:
Δ V ( x ) = V ( x ( k + 1 ) ) − V ( x ( k ) ) = x T ( k + 1 ) P x ( k + 1 ) − x T ( k ) P x ( k ) = x T ( k ) A T P A x ( k ) − x T ( k ) P x ( k ) = x T ( k ) ( A T P A − P ) x ( k ) \begin{aligned} \Delta V(\boldsymbol{x}) &=V(\boldsymbol{x}(k+1))-V(\boldsymbol{x}(k)) \\ &=\boldsymbol{x}^{\mathrm{T}}(k+1) \boldsymbol{P} \boldsymbol{x}(k+1)-\boldsymbol{x}^{T}(k) \boldsymbol{P} \boldsymbol{x}(k) \\ &=\boldsymbol{x}^{\mathrm{T}}(k) \boldsymbol{A}^{\mathrm{T}} \boldsymbol{P} \boldsymbol{A} \boldsymbol{x}(k)-\boldsymbol{x}^{\mathrm{T}}(k) \boldsymbol{P} \boldsymbol{x}(k) \\ &=\boldsymbol{x}^{\mathrm{T}}(\boldsymbol{k})\left(\boldsymbol{A}^{\mathrm{T}} \boldsymbol{P} \boldsymbol{A}-\boldsymbol{P}\right) \boldsymbol{x}(k) \end{aligned} ΔV(x)=V(x(k+1))−V(x(k))=xT(k+1)Px(k+1)−xT(k)Px(k)=xT(k)ATPAx(k)−xT(k)Px(k)=xT(k)(ATPA−P)x(k)
同样设:
Q = − ( A T P A − P ) Q=-(A^TPA-P) Q=−(ATPA−P)
为了让系统渐近稳定,Q应该是正定的。和连续时间系统一样,一般也是先确定Q,然后求解李方程:
A T P A − P = − Q A^TPA-P=-Q ATPA−P=−Q
找到正定的P。同样,有定理5:
定理5:
线性定常离散时间系统渐近稳定的充要条件:对任意给定的正定矩阵Q,存在正定矩阵P,成为李方程的解。
同样,一般取Q为单位阵。
一些例题