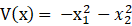1. 背景和思路

系统稳定：系统储存的总能量持续地减小，直至耗尽，系统状态就会趋于平衡态
稳定性考察：考察一个正值的能量函数$V(x)$和它的变化率$\dot{V}(x)$来判断。若$\dot{V}(x)$始终为负，则系统稳定。
困难：对于一般的动态系统，并不是总能明确地定义一个能量函数
解决方案：用一个正定的标量函数作为系统的广义能量函数
这个标量函数是什么：运用李雅普诺夫第二方法判断系统稳定性时，常常采用二次型的标量函数。所谓二次型函数，是指形如
$$V(x)=x^{T}Px$$
的函数，这里P是实对称矩阵。设

则V的正定性可以用西尔维斯特(Sylvester) 准则来判断：
（1）二次型正定：即P矩阵正定：顺序主子式都大于0
（2）二次型（或P）负定：充要：P的主子式满足：

注：
要求正定，则说明V是正值能量函数，要求二次型，则符合能量特征。

2. 李雅普诺夫第二方法

取非线性定常系统状态方程为：
$$\dot{x}(t)=F(x(t))$$
系统平衡状态为：$x_e=0$
定理1：
（寻找李雅普诺夫函数，使得系统渐近稳定）
（1）对于具有连续一阶偏导数的标量函数V(x)，如果V(x)正定，V(x)的导数负定，则系统平衡状态是渐近稳定的，这样的V(x)就是系统的一个李雅普诺夫函数。
（2）如果在（1）成立的情况下，V(x)还满足径向无界条件：

那么平衡状态在整个状态空间中是大范围渐近稳定的。（意义见后面例题）
问题：在定理1中，如果V的导数是半负定的，一般只能确定系统平衡状态在李雅普诺夫意义下是稳定的，但不能确定其渐近稳定性。
解决方案：加一个限制条件，见定理2。
定理2：
（没找到满足定理1的李雅普诺夫函数，但是找到了自身正定、导数半负定的V，也想实现渐近稳定性）
如果V在系统状态方程的任一非零解的状态运动轨迹上不恒为0，那么系统的平衡状态也是渐近稳定的（#跟减函数相似）。如果V径向无界，那么系统是大范围渐近稳定的。

定理3：
（判断系统的不稳定性）
如果找到了有连续一阶偏导数的标量函数V，满足V正定，V的导数也正定，那么系统平衡状态是不稳定的。

3. 李雅普诺夫稳定性分析

对于只有唯一平衡状态的线性定常系统，平衡状态的大范围稳定性与系统的稳定性是一回事，因此就不加区分了。下面将分别介绍用李雅普诺夫第二方法（下称李二法）来分析线性定常连续时间系统和线性定常离散时间系统的稳定性。
（1）线性定常连续时间系统
状态方程：
$$\dot{x}(t)=Ax(t)$$
系统唯一平衡态：$x_e=0$
李函数变化率：

记

为了使系统渐近稳定，Q应该正定。
问题：有时候P选得不好，Q既不是正定的也不是负定的，就不能用李二法判断系统稳定性了。
解决方案：实际用李二法的时候，一般先确定一个正定的Q，然后求解下面的李方程：
$$A^{T}P+PA=-Q$$
再找到正定的P。只要系统是渐近稳定的，那么这个李方程就一定存在正定解。也就是说，已知系统渐近稳定，那么一定存在李函数。这和前面用李函数判断渐近稳定性刚好反过来。这也就有了定理4。
定理4：
线性定常连续时间系统渐近稳定的充要条件：对任意给定的正定矩阵Q，存在正定矩阵P为李方程的解。
因为Q是任意的，所以一般来说，Q取单位阵，最简单了。
（2）线性定常离散时间系统
系统状态方程：$x(k+1)=Ax(k)$
系统唯一平衡态：$x_e=0$
李函数：$V(x)-=-x^{T}Px$
因为是离散时间系统，所以用V(x(k+1))-V(x(k))作为变化率：

同样设：$Q=-(A^{T}PA-P)$
为了让系统渐近稳定，Q应该是正定的。和连续时间系统一样，一般也是先确定Q，然后求解李方程：
$$A^{T}PA-P=-Q$$
找到正定的P。同样，有定理5：
定理5：
线性定常离散时间系统渐近稳定的充要条件：对任意给定的正定矩阵Q，存在正定矩阵P，成为李方程的解。
同样，一般取Q为单位阵。

4. 例题

1. 判断非线性定常系统稳定性：

首先这是二维系统。P是自己选的，要找一个2*2的矩阵。
先确定稳态：两个x的导数都为0，解出来是x1=x2=0，所以稳态是[0,0]’。
P取为I2，得到李雅普诺夫函数：

只要选正定的P，那么V(x)就是正定的，要验证的只是它的导数的负定性：

计算的时候代入x1和x2的导数的表达式就可以。这里a>0，V的导数是负定的。所以平衡状态是渐近稳定的。
另外，当||x||无穷的时候，V也无穷，所以系统在整个状态空间中是大范围渐近稳定的。
大范围渐近稳定的意义：

2. 判断非线性定常系统稳定性：

平衡状态：[0,0]’。
选择P=I2，李雅普诺夫函数：

导数：

只有在x2=0和x2=-1两条直线上，导数为0，所以V的导数是半负定的。

3. 判断线性定常系统稳定性：

平衡状态：[0,0]’
李雅普诺夫函数：

变化率：

所以平衡状态是不稳定的。
4. 判断线性定常系统稳定性：

唯一平衡状态：原点。
取Q为单位阵，则李方程为：

整理成方程组：

因为P是对称的，所以

从而：

利用西尔韦斯特准则，可以得到：

所以P是正定的。所以系统是渐近稳定的。
但这里的Q是指定的，按理说要对任意给定的Q都存在P作为方程的解才行啊，不应该用一般的形式来证明吗？不需要，因为既然找到了合适的P，使得V正定，V的变化率负定，那么系统已经是渐近稳定的了。
5. 求线性定常离散时间系统的稳定性条件：

取Q为单位阵，解李方程：

写成方程组：

考虑P的对称性，解得：

要让P正定，必须满足：

解不等式得到：

这就是线性定常离散时间系统渐近稳定的充要条件了。这和用离散时间系统稳定性代数判据得到的结论是一样的。

5. 参考文献

[1] 田玉平，蒋珉，李世华．自动控制原理[M]．北京：科学出版社，2006