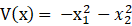稳定性描述系统受到外界干扰，平衡工作状态被破坏后，系统偏差调节过程的收敛性，它是系统正常工作的必要条件。
  经典控制理论用代数判据、奈奎斯特判据、对数频率判据、特征根判据来判断线性定常系统的稳定性，用相平面法来判断二阶非线性系统的稳定性。这些稳定性判据无法满足以多变量、非线性、时变为特征的现代控制系统对稳定性分析的要求。
  李雅普诺夫建立了基于状态空间描述的稳定性理论，提出了依赖于线性系统微分方程的解来判断稳定性的第一方法(间接法)和利用经验和技巧来构造李雅普诺夫函数借以判断稳定性的第二方法(直接法)。李雅普诺夫提出的这一理论是确定系统稳定性的更一般的理论，不仅适用于单变量、线性、定常系统，还适用于多变量、非线性、时变系统。

一、李雅普诺夫稳定性概念

  忽略输入之后，非线性时变系统的状态方程为

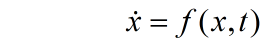
  式中，x为n维状态向量；t为时间变量；f为维函数，假定方程的解为

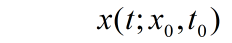
  x0和t0分别是初始状态的状态向量和时刻。

1、平衡状态

  如果对于所有的t，满足：

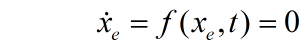
  的状态xe称为平衡状态(平衡点)。平衡状态的各分量不再随时间变化。若已知状态方程，让x的一阶导为0所得到的解x就是平衡点。对于线性定常系统，只要矩阵A非奇异，系统就有唯一的零解，即仅存在一个位于状态空间原点的平衡状态。至于非线性系统，解可能有多个，由系统状态方程决定。
  控制系统李雅普诺夫稳定性理论所指的稳定性是关于平衡状态的稳定性，反映了系统在平衡状态附近的动态行为。鉴于实际线性系统往往只有一个平衡状态，平衡状态的稳定性能够表征整个系统的稳定性。对于具有多个平衡状态的非线性系统来说，由于各平衡状态的稳定性一般不同，需要逐个加以考虑，还需要结合初始条件下的系统运动轨迹来考虑。

2、李雅普诺夫稳定性定义(通俗理解)

（1）李雅普诺夫稳定性(局部稳定)：
  如果平衡状态xe受到扰动后，仍然停留在xe 附近，我们就称xe 在李雅普诺夫意义下是稳定的，也就是说系统初始状态离平衡状态的距离是在 xe 的领域内，过了有限时间，系统动态方程的解离平衡状态的距离仍在epsilon的领域内。如果 delta与t0无关，则称这个平衡状态是一致稳定的。

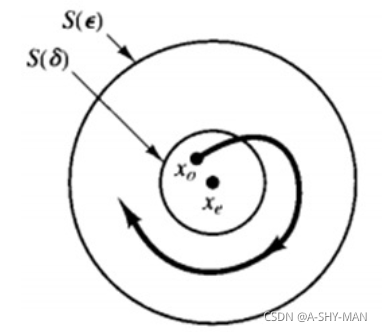
（2）渐进稳定性
  如果平衡状态 xe 受到扰动后，最终都会收敛到 xe ，我们就称 xe 在李雅普诺夫意义下是渐进稳定的，也就是说不仅需要满足李亚普诺夫意义下的稳定性的要求，同时最后这个解要无限逼近平衡状态/平衡点，最后收敛。

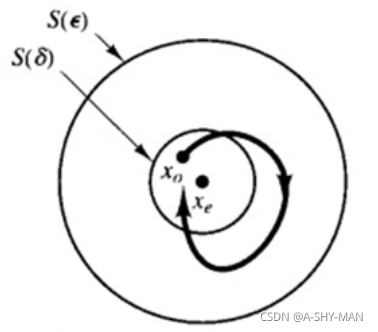
（3）大范围稳定性(全局稳定)
  如果平衡状态 xe 受到任何扰动后，最终都会收敛到 xe ，我们就称 xe 在李雅普诺夫意义下是大范围内渐进稳定的，也就是说从状态空间上任意一点出发，最后都能收敛到平衡状态/平衡点。

（4）不稳定性
  如果平衡状态 xe 受到某种扰动后，状态开始偏离 xe ，我们就称 xe 在李雅普诺夫意义下是不稳定的。

二、李雅普诺夫稳定性间接判别法(第一方法)

间接法是利用状态方程的解的特性来判断系统稳定性的方法，它适用于线性定常、线性时变及可线性化的非线性系统。

  线性定常系统的特征值判据：

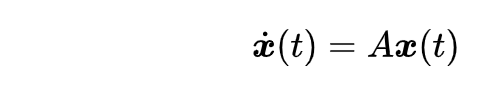
  上述系统渐进稳定的充分必要条件是：系统矩阵A的全部特征值位于复平面左半部。

三、李雅普诺夫稳定性直接判别法(第二方法)

直接法是利用李雅普诺夫函数直接对平衡状态稳定性进行判断，无需求出系统状态方程的解，它适用于各种控制系统。

  一个非常天才的想法,稳定的系统能量总是不断被耗散的,随着时间的推移，系统迟早会到达稳定状态。实际系统的能量函数表达式相当的难找，因此李雅普诺夫引入了广义能量函数，称之为李雅普诺夫函数。

  李雅普诺夫函数：与x1，x2…xn及t相关，是一个标量函数，记为V(x,t)。考虑到能量总大于0，故为正定函数，能量衰减用V(x,t)的一阶导数表示。不过迄今为止没有形成构造李雅普诺夫函数的通用方法，需要经验和技巧。实践表明，对于大多数系统，可先尝试一下的二次型函数作为李雅普诺夫函数。

判断定理：

定理一：V(x,t)正定；V’(x,t)负定；原点渐进稳定。

定理一：V(x,t)正定；V’(x,t)负半定，且在非零状态不恒为0；原点渐进稳定。

定理一：V(x,t)正定；V’(x,t)负半定，且在非零状态恒为0；原点李雅普诺夫稳定。

定理一：V(x,t)正定；V’(x,t)正定；原点不稳定。