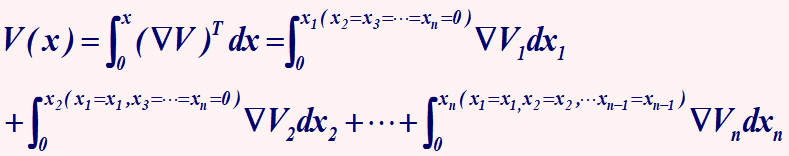原始论文

M.T. Rosenstein, J.J. Collins, and C.J. De Luca. A practical method for calculating largest Lyapunov exponents from small data sets. Physica D, 65:117-134, 1993.

下载地址：https://www.physionet.org/content/lyapunov/1.0.0/

python 相关代码

• NonLinear Time Series Analysis（nolitsa）
  
• NOnLinear measures for Dynamical Systems (nolds)
  

混沌系统的常见指标

区分确定性混沌系统与噪声已成为许多不同领域的重要问题。

对于实验产生的时间序列，可以计算这些混沌系统的指标：

• 相关维数（$D_2$），
• Kolmogorov 熵
• Lyapunov 特征指数。

相关维度是对系统复杂程度的估计，熵和特征指数是对混沌程度的估计。

最大李亚普诺夫指数的含义

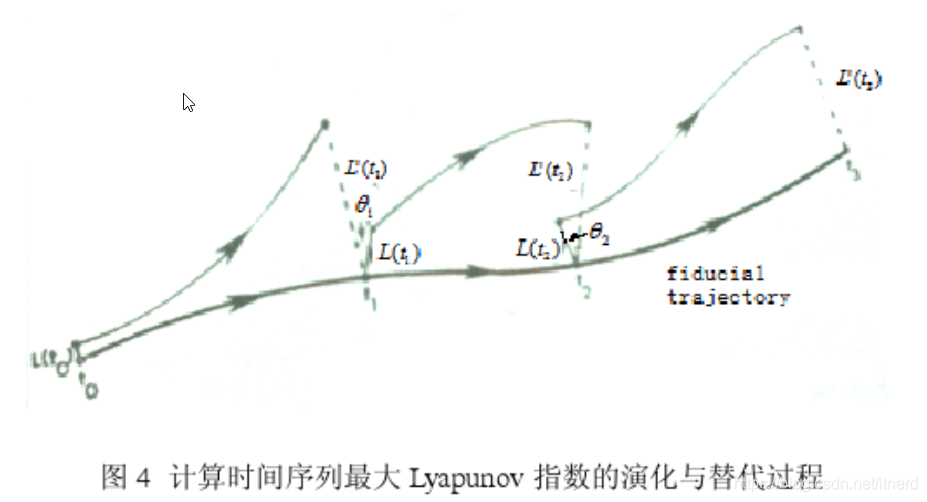
LLE 描述了相空间中相近的两点（初始间距为$C$）随时间推移指数分离的速率：
$$d(t)=C{e}^{{\lambda }_{1}t}$$其中$d(t)$表示分离距离，$C$表示初始间距，${\lambda }_1$ 为最大李氏指数。

算法流程图

python 代码模块

最近邻

import numpy as npfrom scipy import stats
from scipy.spatial import cKDTree as KDTree
from scipy.spatial import distancedef neighbors(y, metric='chebyshev', window=0, maxnum=None):"""Find nearest neighbors of all points in the given array.Finds the nearest neighbors of all points in the given array usingSciPy's KDTree search.Parameters----------y : ndarrayN-dimensional array containing time-delayed vectors.metric : string, optional (default = 'chebyshev')Metric to use for distance computation.  Must be one of"cityblock" (aka the Manhattan metric), "chebyshev" (aka themaximum norm metric), or "euclidean".window : int, optional (default = 0)Minimum temporal separation (Theiler window) that should existbetween near neighbors.  This is crucial while computingLyapunov exponents and the correlation dimension.maxnum : int, optional (default = None (optimum))Maximum number of near neighbors that should be found for eachpoint.  In rare cases, when there are no neighbors that are at anonzero distance, this will have to be increased (i.e., beyond2 * window + 3).Returns-------index : arrayArray containing indices of near neighbors.dist : arrayArray containing near neighbor distances."""if metric == 'cityblock':p = 1elif metric == 'euclidean':p = 2elif metric == 'chebyshev':p = np.infelse:raise ValueError('Unknown metric.  Should be one of "cityblock", ''"euclidean", or "chebyshev".')tree = KDTree(y)n = len(y)if not maxnum:maxnum = (window + 1) + 1 + (window + 1)else:maxnum = max(1, maxnum)if maxnum >= n:raise ValueError('maxnum is bigger than array length.')dists = np.empty(n)indices = np.empty(n, dtype=int)for i, x in enumerate(y):for k in range(2, maxnum + 2):dist, index = tree.query(x, k=k, p=p)valid = (np.abs(index - i) > window) & (dist > 0)if np.count_nonzero(valid):dists[i] = dist[valid][0]indices[i] = index[valid][0]breakif k == (maxnum + 1):raise Exception('Could not find any near neighbor with a ''nonzero distance.  Try increasing the ''value of maxnum.')return np.squeeze(indices), np.squeeze(dists)

maximum Lyapunov exponent

def mle(y, maxt=500, window=10, metric='euclidean', maxnum=None):"""Estimate the maximum Lyapunov exponent.Estimates the maximum Lyapunov exponent (MLE) from amulti-dimensional series using the algorithm described byRosenstein et al. (1993).Parameters----------y : ndarrayMulti-dimensional real input array containing points in thephase space.maxt : int, optional (default = 500)Maximum time (iterations) up to which the average divergenceshould be computed.window : int, optional (default = 10)Minimum temporal separation (Theiler window) that should existbetween near neighbors (see Notes).maxnum : int, optional (default = None (optimum))Maximum number of near neighbors that should be found for eachpoint.  In rare cases, when there are no neighbors that are at anonzero distance, this will have to be increased (i.e., beyond2 * window + 3).Returns-------d : arrayAverage divergence for each time up to maxt.Notes-----This function does not directly estimate the MLE.  The MLE should beestimated by linearly fitting the average divergence (i.e., theaverage of the logarithms of near-neighbor distances) with time.It is also important to choose an appropriate Theiler window so thatthe near neighbors do not lie on the same trajectory, in which casethe estimated MLE will always be close to zero."""index, dist = utils.neighbors(y, metric=metric, window=window,maxnum=maxnum)m = len(y)maxt = min(m - window - 1, maxt)d = np.empty(maxt)d[0] = np.mean(np.log(dist))for t in range(1, maxt):t1 = np.arange(t, m)t2 = index[:-t] + t# Sometimes the nearest point would be farther than (m - maxt)# in time.  Such trajectories needs to be omitted.valid = t2 < mt1, t2 = t1[valid], t2[valid]d[t] = np.mean(np.log(utils.dist(y[t1], y[t2], metric=metric)))return d

RANSAC 拟合曲线

需要先安装 sklearn 库

def poly_fit(x, y, degree, fit="RANSAC"):# check if we can use RANSACif fit == "RANSAC":try:# ignore ImportWarnings in sklearnwith warnings.catch_warnings():warnings.simplefilter("ignore", ImportWarning)import sklearn.linear_model as sklinimport sklearn.preprocessing as skpreexcept ImportError:warnings.warn("fitting mode 'RANSAC' requires the package sklearn, using"+ " 'poly' instead",RuntimeWarning)fit = "poly"if fit == "poly":return np.polyfit(x, y, degree)elif fit == "RANSAC":model = sklin.RANSACRegressor(sklin.LinearRegression(fit_intercept=False))xdat = np.asarray(x)if len(xdat.shape) == 1:# interpret 1d-array as list of len(x) samples instead of# one sample of length len(x)xdat = xdat.reshape(-1, 1)polydat = skpre.PolynomialFeatures(degree).fit_transform(xdat)try:model.fit(polydat, y)coef = model.estimator_.coef_[::-1]except ValueError:warnings.warn("RANSAC did not reach consensus, "+ "using numpy's polyfit",RuntimeWarning)coef = np.polyfit(x, y, degree)return coefelse:raise ValueError("invalid fitting mode ({})".format(fit))

例子：计算洛伦兹系统的最大李雅普诺夫指数

import warnings
from nolitsa import data, lyapunov
import numpy as np
import matplotlib.pyplot as pltdt = 0.01
x0 = [0.62225717, -0.08232857, 30.60845379]
x = data.lorenz(length=4000, sample=dt, x0=x0,sigma=16.0, beta=4.0, rho=45.92)[1]
plt.plot(range(len(x)),x)
plt.show()# Choose appropriate Theiler window.
meanperiod = 30
maxt = 250
d = lyapunov.mle(x, maxt=maxt, window=meanperiod)
t = np.arange(maxt) *dt
coefs = poly_fit(t, d, 1)
print('LLE = ', coefs[0])plt.title('Maximum Lyapunov exponent for the Lorenz system')
plt.xlabel(r'Time $t$')
plt.ylabel(r'Average divergence $\langle d_i(t) \rangle$')
plt.plot(t, d, label='divergence')
plt.plot(t, t * 1.50, '--', label='slope=1.5')
plt.plot(t, coefs[1] +coefs[0]* t, '--', label='RANSAC')
plt.legend()
plt.show()