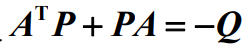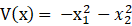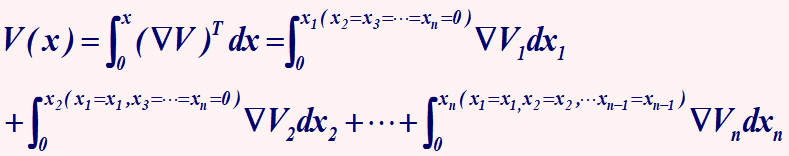研一上学期在现代控制理论课程学习中,接触到了一种题型,“用李雅普诺夫判据判断系统稳定性”,其中判断给定非线性系统大范围渐近稳定上来就是四个步骤,记录一下自己的理解。
不论述完整内容,仅表达一些问题看法和思考角度。
基本知识:
李雅普诺夫稳定性定理:
正定;
负定;
- 当
时,
,
则证明给定的非线性系统原点平衡状态大范围渐进稳定。
那么,选取的候选Lyapunov函数正定易知,这个
你让他乖乖负定还真难搞。总有些不乖的情况,
半负定/负半定了,上述李雅普诺夫判据不好用了。
第一个理解点:
- 正定:
;
- 负定:
;
- 半负定(有省略):说白了,本来只有x=0能让我的导数为0。现在除了0以外,有其他奇怪的点让导数为0了。
没有科学家们解决不了的问题,于是出现了广义能量函数。只要:
,
然后巴拉巴拉,系统还是大范围渐近稳定的。什么意思啊,怎么就不恒为零就可以了?
第二个理解点:
系统的能量是衰减的,最终都会衰减到零。
有奇怪的点让我的导数为零,系统能量不衰减了?我还没衰减到零啊喂!
把奇怪的点带到状态方程中看一看,发现使得状态方程为零的点还是只有原点而已。哦还好还好,奇怪的点只是让我系统的能量一段时间不变化、不衰减而已(即不恒为零中等于零的时候),最终我系统的能量还是会衰到零的,这在控制系统里还是比较常见的。所以,系统:我还是大范围渐近稳定的~( ̄▽ ̄)~*。
封面图片来自:知乎 J Pan
如果此篇文章对您有帮助,记得评论告诉我:) 您的点赞和收藏是对写作者最大的鼓励~