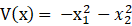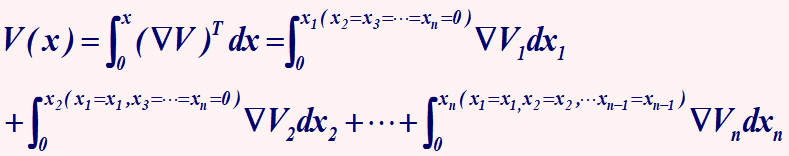如何理解和计算Lyapunov exponent spectrum?
1、这是我听到最接近人话的描述。
混沌运动的基本特点是运动对初始条件极为敏感,两个极为靠近的初始值所产生的轨迹,随着时间推移将按照指数方式分离。李娜诺普指数就是描述这一现象的量。
2、


结论:

-----

----
计算方法来了:




求解指数的这一块内容,实在没有看懂,必须得结合code
------------------

% 计算李雅普诺夫指数
clear all;
hold on
alpha0=3:0.001:4;
N=1000;
for j=1:length(alpha0)
alpha=alpha0(j);
x0=0.1;%初始值
s=0;
for ii=1:N
df=alpha-2*alpha*x0;
s=s+log(abs(df));%lambda叠加
x0=alpha*x0*(1-x0);%x迭代
end
Lm(j)=s/N;% 指数
end
plot(alpha0,Lm,'r')
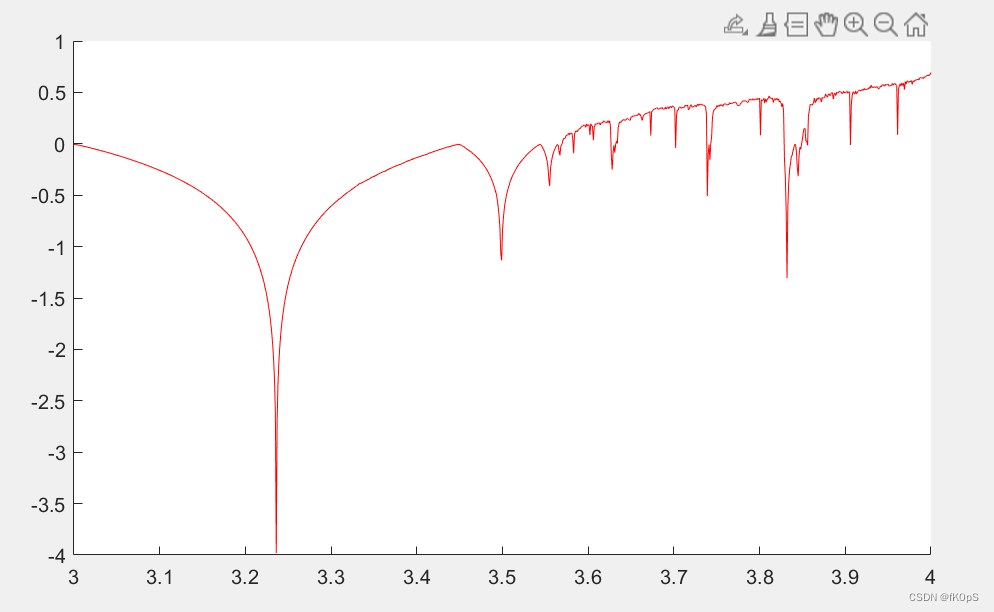
当alph大于3.6的时候,系统已经要进入混沌态了,此时lamda大于0
下图的展示更加直观;

-------------------
李雅普诺夫指数_百度百科

----
matlab 计算 Lorenz 系统最大李雅普诺夫指数_颹蕭蕭的博客-CSDN博客_最大李雅普诺夫指数


这个是计算李雅普诺夫指数的真实code
matlab 计算 Lorenz 系统最大李雅普诺夫指数_颹蕭蕭的博客-CSDN博客_最大李雅普诺夫指数