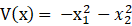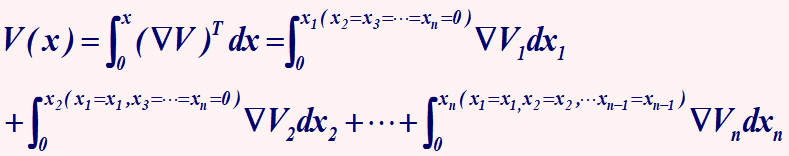李雅普诺夫稳定性matlab仿真程序

李雅普诺夫稳定性判别有两种方法，直接法和间接法。直接法是求解状态方程的特征多项式，判断极点位置，全在左半平面则稳定。间接法是最常用的判断稳定性方法，无需求解，只要构造一个广义李雅普诺夫函数V，使得V正定，而V负定（半负定还需进一步判断），但是V的构造常常不容易，计算机求解常用.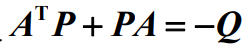

一、直接法

以四阶状态方程为例

A=[-3 -6 -2 -1;1 0 0 0;0 1 0 0;0 0 0 1];
B=[1;0;0;0];
C=[0 0 1 1];		%状态矩阵
[~,namda]=eig(A);   %求解特征值
P=diag(namda);
real(P)  			%特征值取实部
if(P<0)a='特征值实部均小于0，系统在平衡点渐进稳定'
elsea='存在特征值实部大于0，系统不稳定'
end

二、间接法

以三阶状态方程矩阵为例

A=[1 -3.5 4.5;2 -4.5 4.5;-1 1.5 -2.5];
B=[-0.5 -0.5 -0.5];
C=[1 0 1];				%状态方程矩阵
Q=eye(3);
P=lyap(A.',Q)
if(P(1,1)>0&&det(P(1:2,1:2))>0&&det(P)>0)a='P正定，故系统在平衡位置渐进稳定'
elsea='P非正定，故系统在平衡位置不稳定'
end

matlab内部已经有封装好的函数，直接调用就可以。