ER模型
数据库设计是牵一发而动全身的。那有没有什么办法提前看到数据库的全貌呢?比如需要哪些数据表、数据表中应该有哪些字段,数据表与数据表之间有什么关系、通过什么字段进行连接,等等。这样我们才能进行整体的梳理和设计。
其实,ER模型就是一个这样的工具。ER模型也叫作实体关系模型,是用来描述现实生活中客观存在的事物、事物的属性,以及事物之间关系的一种数据模型。在开发基于数据库的信息系统的设计阶段,通常使用ER模型来描述信息需求和信息特性,帮助我们理清业务逻辑,从而设计出优秀的数据库。
1.ER模型包括哪些要素
ER模型中有三个要素,分别是实体、属性和关系。
实体,可以看做是数据对象,往往对应于现实生活中的真实存在的个体。在ER模型中,用矩形来表示。实体分为两类,分别是强实体和弱实体。强实体是指不依赖于其他实体的实体;弱实体是指对另一个实体有很强的依赖关系的实体。
属性,则是指实体的特性。比如超市的地址、联系电话、员工数等。在ER模型中用椭圆形来表示。
关系,则是指实体之间的联系。比如超市把商品卖给顾客,就是一种超市与顾客之间的菱形。在ER模型中用菱形来表示。
注意:实体和属性不容易区分。这里提供一个原则:我们要从系统整体的角度出发去看,可以独立存在的是实体,不可再分的是属性。也就是说,属性不能包含其他属性。也就是说,属性不能包含其他属性。
2、关系的类型
在ER模型的3个要素中,关系又可以分为3种类型,分别是一对一、一对多、多对多。
一对一∶指实体之间的关系是一一对应的,比如个人与身份证信息之间的关系就是一对一的关系。一个人只能有一个身份证信息,一个身份证信息也只属于一个人。
一对多∶指一边的实体通过关系,可以对应多个另外一边的实体。相反,另外一边的实体通过这个关系,则只能对应唯一的一边的实体。比如说,我们新建一个班级表,而每个班级都有多个学生,每个学生则对应一个班级,班级对学生就是一对多的关系。
多对多∶指关系两边的实体都可以通过关系对应多个对方的实体。比如在进货模块中,供货商与超市之间的关系就是多对多的关系,一个供货商可以给多个超市供货,一个超市也可以从多个供货商那里采购商品。再比如一个选课表,有许多科目,每个科目有很多学生选,而每个学生又可以选择多个科目,这就是多对多的关系。
3、建模分析
ER模型看起来比较麻烦,但是对我们把控项目整体非常重要。如果你只是开发一个小应用,或许简单设计几个表够用了,一旦要设计有一定规模的应用,在项目的初始阶段,建立完整的ER模型就非常关键了。开发应用项目的实质,其实就是建模。
我们设计的案例是电商业务,由于电商业务太过庞大且复杂,所以我们做了业务简化,比如针对SKU(StockKeepingUnit,库存量单位)和SPU(Standard Product Unit,标准化产品单元)的含义上,我们直接使用了SKU,并没有提及SPU的概念。本次电商业务设计总共有8个实体,如下所示:
- 地址实体
- 用户实体
- 购物车实体
- 评论实体
- 商品实体
- 商品分类实体
- 订单实体
- 订单详情实体
其中,用户和商品分类是强实体,因为它们不需要依赖其他任何实体。而其他属于弱体,因为它们虽然都可以独立存在,但是它们都依赖用户这个实体,因此都是弱实体。知道了这些要素,我们就可以给电商业务创建ER模型了,如图:
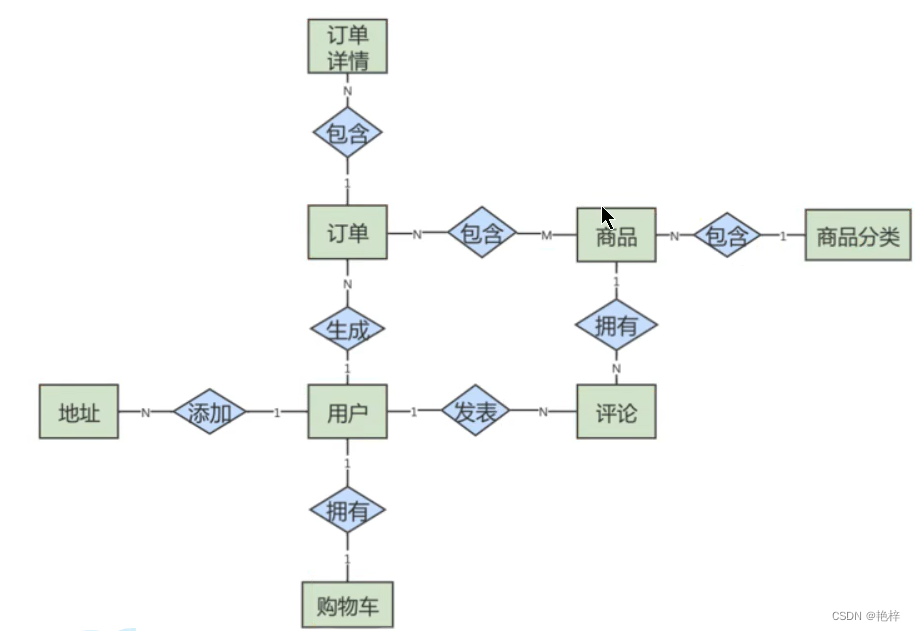
4、ER模型细化
有了这个ER模型,我们就可以从整体上理解电商的业务了。刚刚的ER模型展示了电商业务的框架,但是只包括了订单,地址,用户,购物车,评论,商品,商品分类和订单详情这八个实体,以及它们之间的关系,还不能对应到具体的表,以及表与表之间的关联。我们需要把属性加上,用椭圆来表示,这样我们得到的ER模型就更加完整了。
因此,需要进一步去设计一下这个ER模型的各个局部,也就是细化下电商的具体业务流程,然后把它们综合到一起,形成一个完整的ER模型。这样可以帮助我们理清数据库的设计思路。
接下来,再分析一下各个实体都有哪些属性,如下所示:
(1)地址实体包括用户编号、省、市、地区、收件人、联系电话、是否是默认地址。
(2)用户实体包括用户编号、用户名称、昵称、用户密码、手机号、邮箱、头像、用户级别。
(3)购物车实体包括购物车编号、用户编号、商品编号、商品数量、图片文件url。
(4)订单实体包括订单编号、收货人、收件人电话、总金额、用户编号、付款方式、送货地址、下单时间。
(5)订单详情实体包括订单详情编号、订单编号、商品名称、商品编号、商品数量。
(6)商品实体包括商品编号、价格、商品名称、分类编号、是否销售,规格、颜色。
(7)评论实体包括评论id、评论内容、评论时间、用户编号、商品编号
(8)商品分类实体包括类别编号、类别名称、父类别编号
这样细分之后,就可以重新设计电商业务了,ER模型如图:
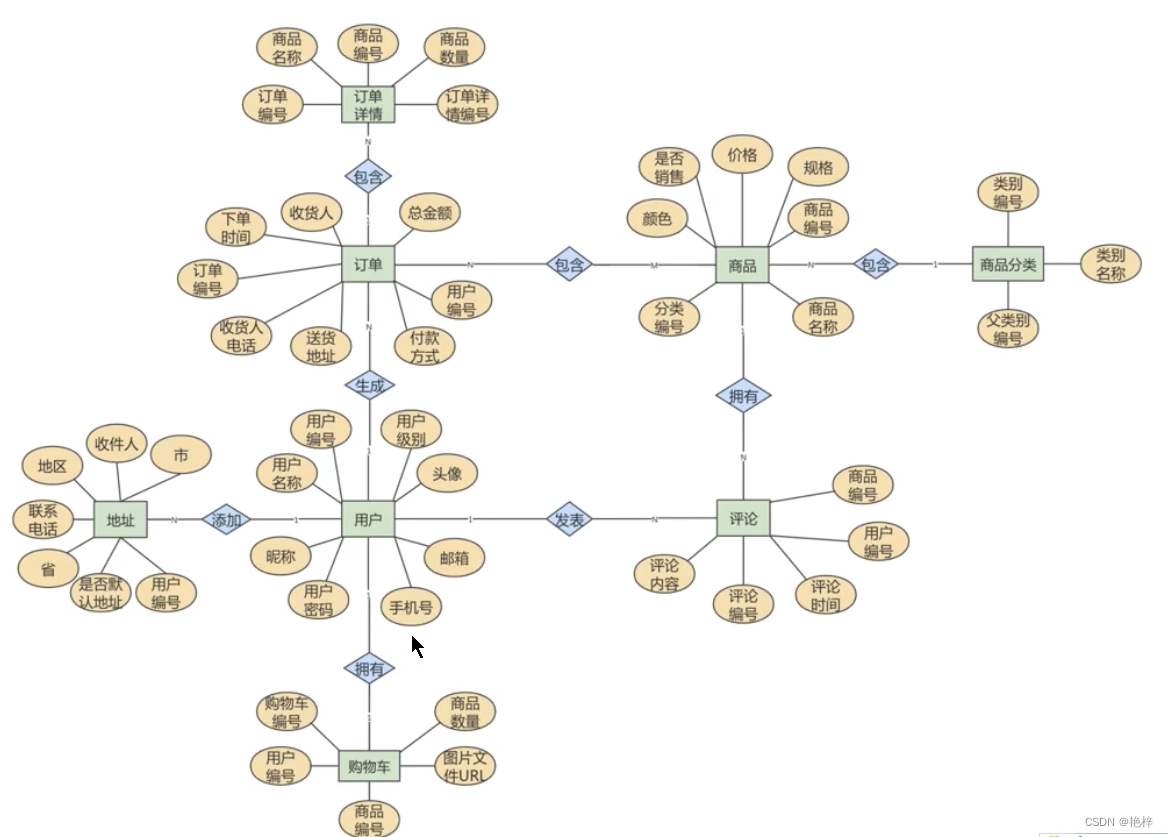
5、ER模型图转换成数据表
通过描绘ER模型,我们已经理清了业务逻辑,现在,我们就要进行非常重要的一步了:把绘制好的ER模型,转换成具体的数据表,下面介绍下转换的原则:
(1)一个实体通常转换成一个数据表;
(2)一个多对多的关系,通常也转换成一个数据表;
(3)一个1对1,或者1对多的关系,往往通过表的外键来表达,而不是设计一个新的数据表;(4)属性转换成表的字段。