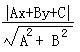一、（低通）采样定理

• 如何从抽样信号中恢复原连续信号、在什么条件下才可以无失真地由采样信号恢复原连续信号，著名的采样定理对此作了明确的回答。

• 采样定理在通信系统、信息传输理论、数字信号处理等方面占有十分重要的地位，该定理在连续时间信号与系统和离散时间信号与系统、数字信号与系统之间架起了一座桥梁。

• 该定理从理论上回答了为什么可以用数字信号处理手段解决连续时间信号与系统问题。

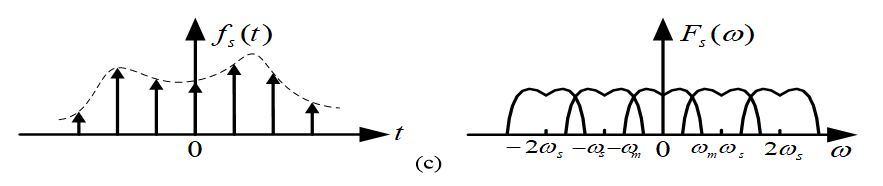
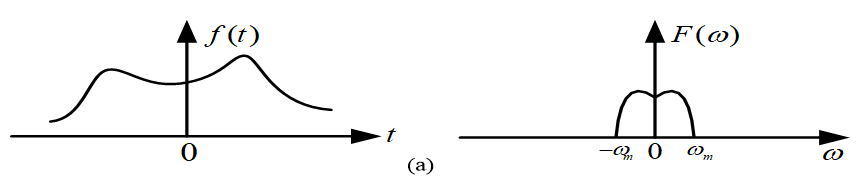
抽样信号的频谱及频谱混叠现象

1、连续信号及其频谱

2、高抽样频率时的抽样信号及其频谱 

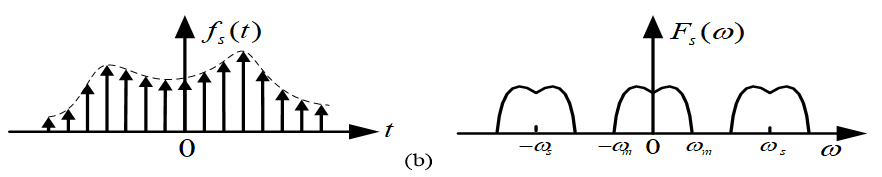
3、低抽样频率时的抽样信号及其频谱

不满足抽样定理时产生频率混叠现象

时域抽样定理：

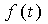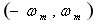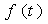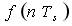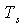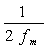时域抽样定理表明，一个频谱受限的信号， 如果频谱只占据的范围，则信号 可以用等间隔的抽样值唯一地表示，只要抽样间隔不大于， 其中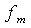为信号的最高频率，或者说，抽样频率满足条件。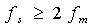

通常把满足抽样定理要求的最低抽样频率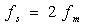称为奈奎斯特频率，把最大允许的抽样间隔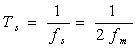称为奈奎斯特间隔。

 

---

二、带通采样定理

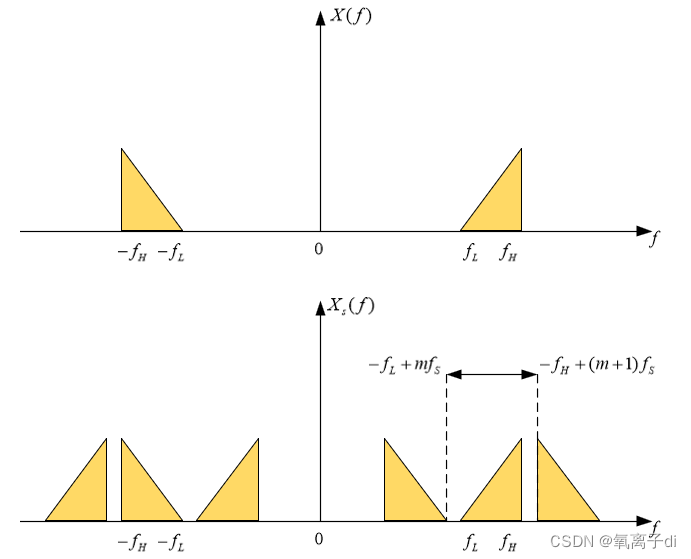
实际中遇到的许多信号是带通型信号。如果采用低通抽样定理的抽样速率fs≥2fH，对于频率限制在fL与fH之间的带通型信号抽样，肯定能满足频谱不混叠的要求。但这样选择fs太高了，它会使0~fL一大段频谱空隙得不到利用，抽样后的信号速率很高，降低了信道的利用率。

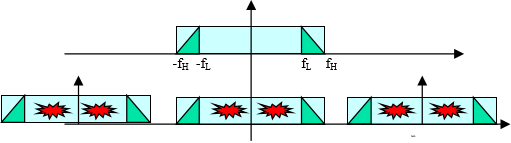
那么，能否降低抽样频率？

对带限信号采样时，若其下限频率fL, 上限频率为fH时:

为使采样后的频域不发生混叠，需要使信号负频域的分量经过m-1次和m次平移后得到的频谱曲线不能与信号原本的正频域分量重叠，因此必须满足下式：

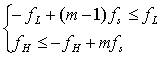
对上式进行变换，可得

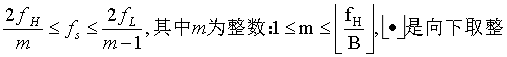
从上面的结论中可以看出，当m取1时，正好是奈奎斯特采样定理。对于带通信号，没有必要使采样频率高于信号频率上限的两倍，若信号最高频率f_H为信号带宽的整数倍时，采样频率只需大于或等于信号带宽的两倍即可，而不会发生频谱混叠。

fs的计算例子，以30M-40M的信号为例，fH=40M，fL=30M，B=10M；当：

                    m=1时，80M<=fs<=∞；（低通采样定理）

                    m=2时，40M<=fs<=60M；

                    m=3时，26.6M<=fs<=30M；

                    m=4时，20M<=fs<=20M；（m取得最大值）

以上3个区间内的任意频率都可以进行频谱不混叠的带通采样。