前言

2022年电赛F题-信号调制度测量装置说明中提到带通采样定律。

低通采样定理在《信号与系统》教材中进行了详细的讨论，但未对带通信号的采样定理进行描述，国内樊昌信和曹丽娜老师编写的《通信原理》第10章第2小节有所描述，但没有详细的公式推导，容易给初学者产生~~超过该最低采样频率即不会产生频谱混叠的假象~~

一、采样定理？

芯片只能处理数字信号，而现实生活中的很多信号是模拟信号，因此需要将模拟信号转换为数字信号。在转换过程中需要三个步骤：采样、量化、编码。

采样：又称为抽样或取样，把时间连续的信号转换为时间不连续的脉冲。该脉冲信号称为采样信号，采样信号在时间轴上是离散的，但在幅度（y轴）上仍是连续的。把采样信号变为在时间上离散，在幅度上也离散的过程叫作量化。
量化：是一个数值分层过程，即四舍五入过程。
编码：是将量化后的数字信号的幅值，变换成一组组对应的二进制数组。

第一步的采样最为关键，关系到模数转换，再到数模转换。经过几次变换，传输的信号还要保持不变，这样的通信才算完整可靠。

采样定理说明采样频率与信号频谱之间的关系，是连续信号离散化的基本依据。其采样频率能捕获连续时间信号的所有信息。

1.低通采样定理（奈奎斯特采样）

低通采样定理（奈奎斯特采样）是要求大于信号的最高上限频率的两倍
提示：此采样定理是万能的，理论上可利用此定理对带通信号采样。

2.带通采样定理

带通信号的采样频率在某时，小于低通采样频率也能无失真恢复原信号

二、频谱混叠

对一个连续时域信号，采样后变为时域离散但幅值连续的采样信号。根据傅里叶理论，连续非周期信号对应的频域曲线是非周期连续的波形，而离散非周期信号对应的频域曲线是周期连续的波形。

所以采样本质就是对原信号进行周期性的频谱搬移。故采样频率没选好，就会使周期性频谱搬移过程中造成频谱混叠，既然频谱和原信号的频谱对不上了，故就无法无失真恢复原信号了，总之，频域波形不出现重叠是无失真传输的重要保障。
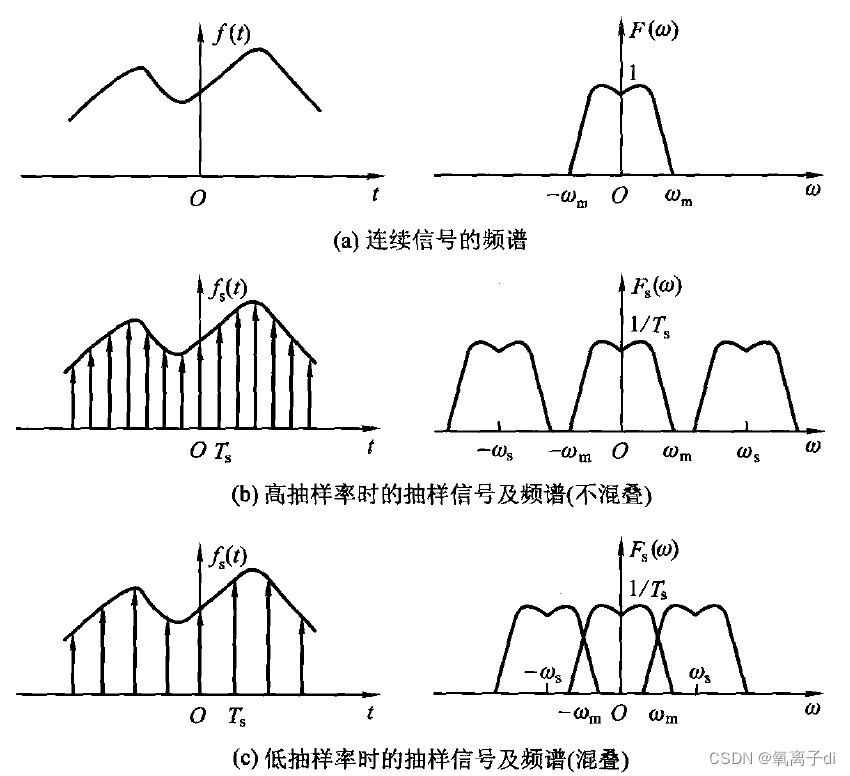
在这里插入图片描述
设采样角频率是 $w_s$ ，原信号的最高上限角频率是 $w_m$

由上图可见采样就是以周期 $T_s$ 进行频谱搬移，显然， $\ w_s\geqslant 2w_m$ 就不会造成频率混叠，这就是奈奎斯特采样。物理上解释，一个频带受限信号波形不可能短时间产生独立的，实质的变化，最高变化速度受最高频率分量的限制，因而为了保留这一频率分量的信息，故一周期内至少采样两次。

三、带通采样定理

奈奎斯特采样定理讨论的是频谱分布在( 0, $f_H$ )上的基带信号的采样问题。但对于接收机，接收信号大多为调制的射频信号，射频信号的频率上限远高于基带信号的频率上限，且仅分布在有限的( $f_L$ , $f_H$ )范围内。

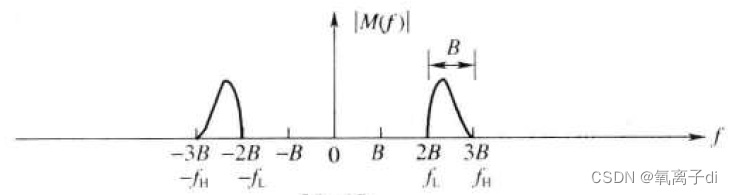
上图为带通信号的频谱图（一般都是已调信号）

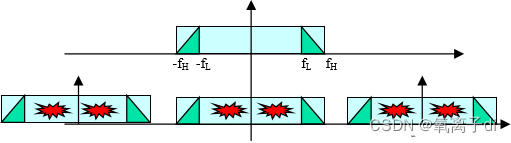
请添加图片描述
对带通信号采用低通抽样定理抽样，也不会造成频谱混叠，但会发现0~ $f_L$ 区间频谱没有使用，且一般 $f_H$ 很大，所以采样率很高，大大降低了信道的利用率

现实生活中信号带宽 $B$ 并不一定很宽可能为几M，但 $f_H$ 可能为几十个G，AD也难以实现如此高的采样率，这时，低通采样定理已经不能满足实际中的使用要求，从而催生了带通采样的应用。

带通采样定理：设带通信号频带仅在( $f_L$ ~ $f_H$ )之间，信号带宽即为 $B=\ f_H-\ f_L$ ，则最小采样速率 $f_{s}=2B(1+\frac{k}{n} )$ ，其中 $k$ 为 $\frac{f_{H}}{B}$ 的小数部分， $n$ 为 $\frac{f_{H}}{B}$ 的整数部分
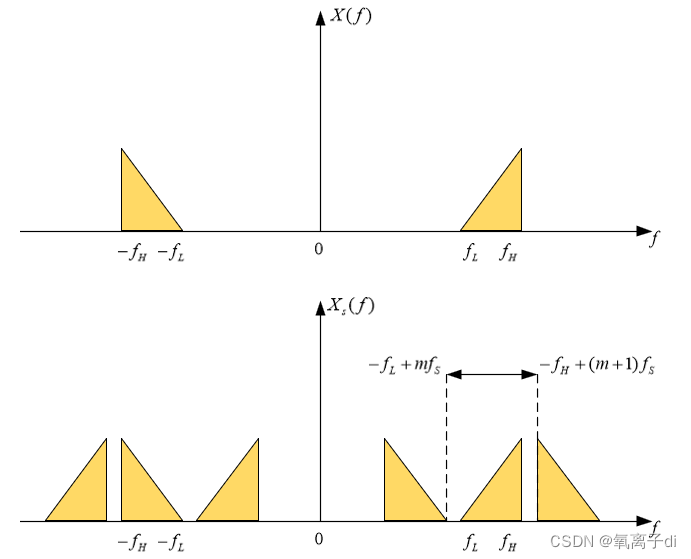
在这里插入图片描述
现推导带通采样定理：
由于带限信号频谱具有轴对称性，故只需分析一边。如上图，为避免频谱混叠，
$\begin{cases}-f_{L}+mf_{s} \le f_{L} \\f_{H}\le -f_{H}+(m+1)f_{s} \end{cases}$

不难求得采样频率 $f_{s}$ 的取值范围
$\frac{2f_{H}}{m+1} \le f_{s}\le \frac{2f_{L}}{m}$ ，( $m$ 为非负整数，其含义是m次频移)

显然 $f_{s}$ 存在的条件是 $\frac{2f_{H}}{m+1} \le \frac{2f_{L}}{m}$ ，化简可知 $\ m \le \left \lfloor \frac{f_{L}}{f_{H}-f_{L}} \right \rfloor$ ，（ $\left \lfloor ·\right \rfloor$ <->向下取整）

$\ m$ 的意义：在[ $\ 0$ ~ $f_L$ ]范围内容纳的频谱数
解释：
设 $m_{max}$ 在[ $\ 0$ ~ $f_L$ ]范围内最多容纳的频谱数， $m_{max}$ 必须为整数
则 $\ m_{max}\times (f_{H}-f_{L}) \le f_{L}$ ，即 $\ m_{max}\times B \le f_{L}$

现推导最小采样频率：
最小采样频率即为 $\frac{2f_{H}}{m+1}$ ，且 $\ m=m_{max}=[ \frac{f_{L}}{f_{H}-f_{L}} ]$

①当 $f_{H}$ 不是带宽B的整数倍时，可用 $\ f_H=n\times B +k\times B$ 表达，其中 $n$ 为 $\frac{f_{H}}{B}$ 的整数部分， $k$ 为 $\frac{f_{H}}{B}$ 的小数部分

$\ m_{max}+1= \frac{f_{H}}{f_{H}-f_{L}}= \frac{f_H}{B}=n$

故 $\frac{2f_{H}}{m_{max}+1} = \frac{2f_H}{n}=2B(1+\frac {k}{n})$

②当 $f_{H}$ 是带宽B的整数倍时，可用 $\ f_H=n\times B 表达，其中n$ 为 $\frac{f_{H}}{B}$ 的整数部分
同理可知， $\frac{2f_{H}}{m_{max}+1} = \frac{2f_H}{n}=2B$

四、带通采样的限制条件

只允许在其中一个频带上存在信号，而不允许在不同的频带同时存在信号，否则将会引起信号混叠。

五、误区

本人建议在利用带通采样的时候，用不等式 $\frac{2f_{H}}{m+1} \le f_{s}\le \frac{2f_{L}}{m}$ 确定采样频率。

千万不要也不能理解为采样频率超过最小值 $\frac{2f_{H}}{m+1}$ 后，就不会产生频谱混叠。
带通采样定理的采样频率的取值是不连续的分段区间，故应注意与低通信号的最小采样频率进行区别理解。

六、总结

带通采样的核心就是频谱搬移，搬移到低频带上进行采样。故带通采样大大降低了所需的采样频率，为后面的实时处理奠定了基础。另外，当对于一个频率很高的射频信号采样时，如果采样频率设的太低，对提高采样量化的信噪比是不利的。所以，在可能的情况下，带通采样频率应该尽可能选的高一些，使瞬时采样带宽尽可能宽。

七、参考资料

Cheeky_man.低通采样定理与带通采样定理
数字化的重要理论：带通采样定理
[1]王兵锐,张新刚,马晓普.通信教学研究中带通采样的统一推导与验证[J].现代信息科技,2019,3(24):55-57.DOI:10.19850/j.cnki.2096-4706.2019.24.017.
[2]黄喜军,陈辉金.带通信号采样定理的教学浅析[J].电气电子教学学报,2011,33(04):104-105.