CSDN话题挑战赛第2期
参赛话题:学习笔记
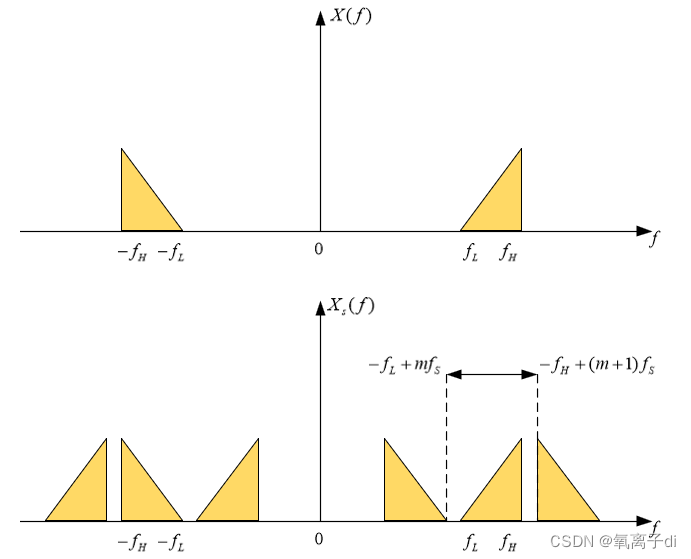
数据采集的最主要功能之一是将外部模拟信号转换为离散信号传递到计算机中去,这一过程被称为采样。采样频率或采样率,即每秒采集所得的数据个数,对于采样过程是一个至关重要的参数,确定了合适的采样频率,才可能在数据采集设备允许的性能范围和硬设备成本下,进行正确而可靠的采样。
过高的采样频率显然会增加采集设备的工作负担及软件计算的工作量,另外也会增加硬件采购成本。而过低的采样频率不足以正确恢复原始信号,采样定理(又称奈奎斯特定理,Nyquist定理)指出,采样频率必须至少是原始信号中所包含最高频率的两倍时,所得到的采样信号才能包含原始信号所有频率分量的全部信息,否则从采样信号恢复原信号时将发生畸变。
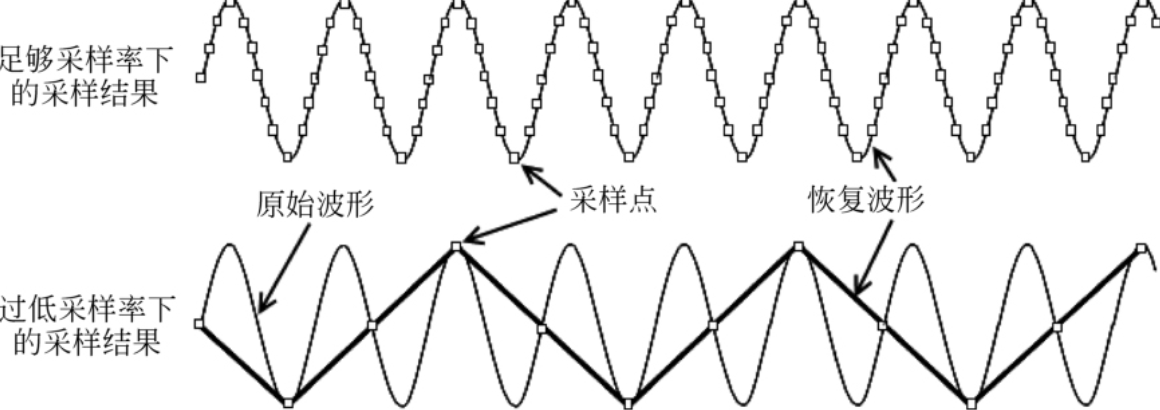
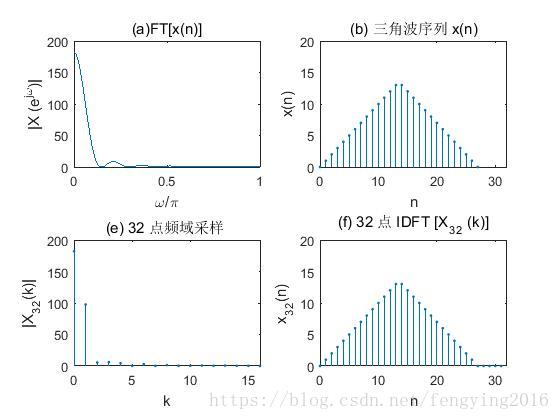
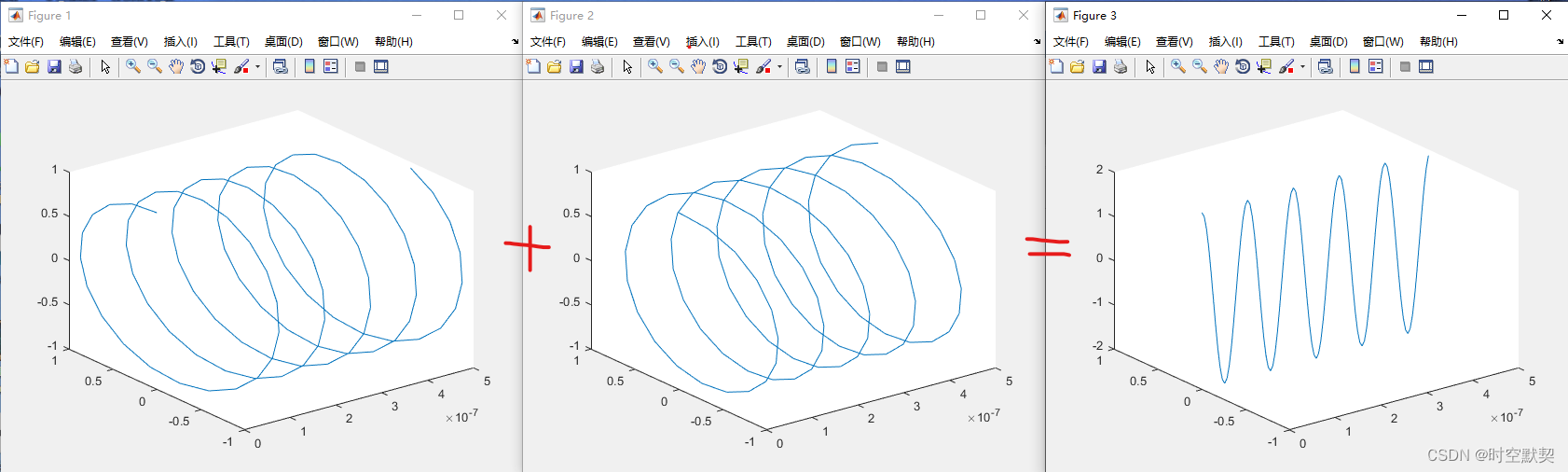
分别使用足够的采样频率和过低的采样频率,所得到的采样信号结果,可以看出,采样频率过低时得到的信号有可能导致错误的恢复结果,即信号畸变。
这种信号畸变也称混叠(alias),理论上只要采样频率达到信号所包含最高频率的2倍以上就可避免混叠,但是工程应用上往往要留出一些裕量,一般取5~10倍,如果对信号处理效果有更高要求,甚至还需取得更高。
在实际应用中,即使已经知道待采集信号的最大频率值,但受环境噪声和通道干扰影响,(如交流输电线路的50Hz信号干扰,以及附近电焊或超声波焊接可能带来的超高频干扰),会带来很高频率的干扰信号,混杂于有用信号中从而产生混叠,影响采集效果。
为解决此类问题,通常在采样器和模拟/数字转换器(ADC)之间加一个低通滤波器,可以保证低频信号通过并且衰减高频信号,从而保证所有频率分量都在适当的范围内。
执行这种功能的滤波器常被称为抗混叠滤波器,许多数据采集卡或数据采集设备都已经通过硬件方式实现了抗混叠滤波器。
一个理想的抗混叠滤波器的频响特性是呈阶跃式的,如图所示,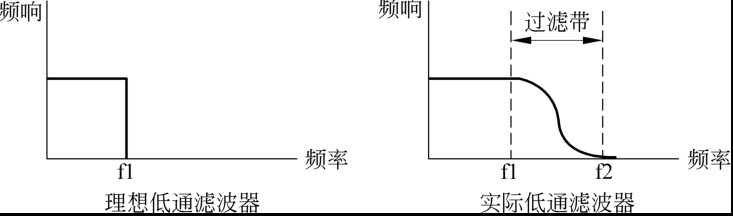
但实际上理想滤波器无法以有限的成本实现,所以一般应用的是频响特性具有过渡带的滤波器
对于低于频率f1的所有信号都可以不受衰减地通过,而高于频率f2的所有信号都被阻挡,在f1和f2之间的信号按照过渡带特性部分衰减地通过。显然,f2应该在采样频率的一半以内,才不致产生混叠,实际应用中更需多留出些余量。
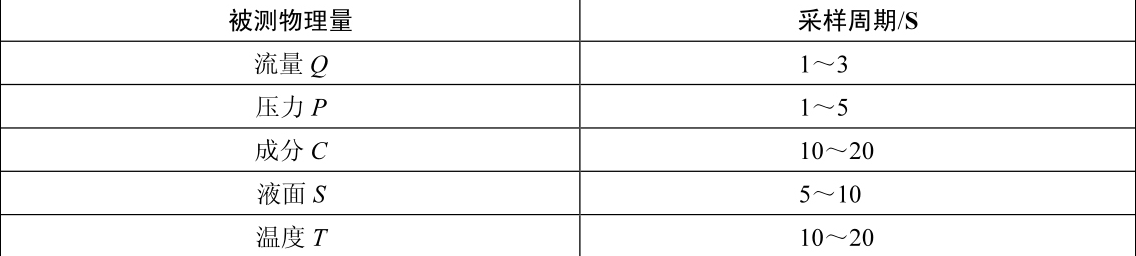
在实际工作中,考虑到实际的模拟低通滤波器不可能有理想的截止特性,在其截止频率fh之后总有一定的过渡带,故采样频率常选为(3~4)fh,甚至更高。采样频率的选择是一个非常重要的问题,由于被测对象多种多样,采样频率的选择又是一个比较困难的问题。数据采集在各领域的应用已十分普遍,对采样频率的选取也积累了很多经验,表列出了一些被测物理量采样频率选取的经验实现范围。