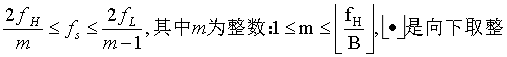连续时间采样及采样定理—

一、实验目的

1、掌握连续时间信号离散化的方法（即采样）,并能利用Matlab编程加以仿真实现;
2、掌握连续时间信号的傅立叶变换和离散时变换的仿真实现方法；
3、学会利用傅里叶变换和离散时间信号的傅立叶变换的方法对连续时间信进行频谱的分析;
4、掌握连续时间信号经理想采样后信号的频谱变化;
5、验证带限信号的时域采样定理，并加深对定理及与其相关的概念、名词的理解

二、实验原理

1、连续时间信号的采样
连续时间信号xa(t)以时间间隔T (即采样周期)采样后所得到的离散时间信号可表示为xa(nT),即xa(t)只保留t=nT时的值，这里n只能取整数。从数学观点而言，时间间隔T对离散时间信号的各采样点只起间隔大小的作用，对顺序无作用，因而xa(nT)还可表示为x(n)。则采样后所得到的离散时间信号x(n)与其对应的连续时间信号xo (t)的关系可表示为:
x(n)=xa(t)|t=nT
对连续时间信号进行采样得到离散时间信号的过程，在Matlab中以对e 100进行均匀采样为例，可用如下代码来进行实现:

Ts=0.0005;%设置采样周期
n=-25:1:25; %设置采样的起始时刻点
x=ex1(1000*abs(n*Ts));%按公式给定的连续时间信号得到离散时间信号xn

2、采样后信号频谱的变化
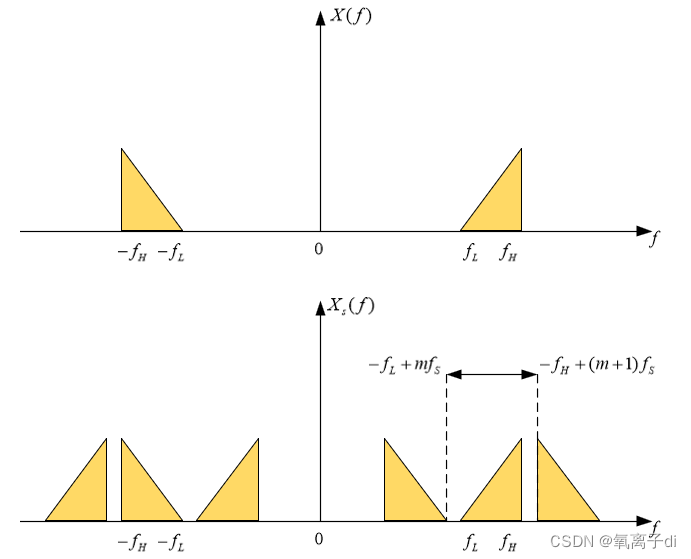
从频域的角度来看，采样前后的信号频谱也是不一样的，采样后的信号频谱Xs(jΩ)是采样之前的信号频谱Xa(jΩ)的周期延拓，延拓周期为2π/T。同时，Xs(jΩ)的幅度是Xa(jΩ)的幅度的fs=1/T倍。即:
在这里插入图片描述

假定Xa(jΩ)是带限信号,画出了上述的关系:
在这里插入图片描述

3、时域采样定理
从频域的角度分析，并结合图2.1，要保证信号采样不丢失信息，则需避免频谱的混叠失真。那么，在被采样信号是带限信号的前提下，对采样周期了(或采样频率f) 就要有一定的要求，这要求即为时域采样定理。时域采样定理也称为奈奎斯特采样定理，可描述为:对一个有限带宽信号进行采样，如果采样顿率大于或等于信号最高频幸两倍时，得到的采样信号频请是原信号频增无混叠失真的周期延拓，因此可以由采样后的信号恢复原信号。
4、傅立叶变换的计算机计算方法
信号的频域分析是信号分析的基本手段之一。对信号进行频谱分析，从数学上讲就是进行傅立叶变换，对于连续时间信号而言，傅立叶变换公式是积分形式，具体如下:
X(jΩ)=∫_(-∞)^(+∞)▒〖x(t) e^(-jΩt) dt〗

而对于离散时间信号(序列)而言，傅立叶变换公式为求和的形式，具体如下:
X(e^jω )=∑_(n=-∞)^n∞▒〖x(n) e^(-jωn) 〗

不管是连续时间信号还是离散时间信号，频谱一般都是关于频率的连续函数，即均为连续谱。在Matlab中，积分一般采用离散化的求和方式进行近似计算，而求和则可借助矩阵乘法进行。因而中的积分和公式(2-4) 中的求和都可以借助矩阵乘法运算进行实现，具体计算及画图程序示例如下:
(1)连续时间信号的傅立叶变换

Dt=-0.0005;t=-0.005:Dt:0.005;
Xa=exp(-1000*abs(t));%生成连续时间信号
Wmax=2*pi*2000;500;k=0:1:K;W=k*Wmax/K;
Xa=xa*exp(-j*t’*W)*Dt%/续时间信号的傅位叶变换
Xa=abs(Xa);
W=_flipIr(W),W(2:501)]; Xa=[fliplr(Xa),Xa(2:501)];
plot(W/(2*pi* 1000),Xa* 1000);
xlabel(频率(KHZ) ); ylabel(Xa(jW));

(2)离散时间信号的傅里叶变换

Ts=0.0005;n=-25:1:25;
x-exp(-1000* abs(n* Ts)); %对连续时间信号进行理想采样
K=500;k=0:1 :K;w=pi*k/K;
X=x*exp(j*n'*w); %离散时间傅立叶变换
X= abs(X);
w=[-fliplIr(w),w(2:K+1)]; X=[flipIr(X),X(2:K+1)]; 
plot(w/pi,X); xlabel(频率(rad));ylabel(X1(w));

三、实验步骤、数据记录及处理

本实验以信号的采样为基础，借助傅立叶变换进行采样前后信号的频谱分析，在此基础上验证时域采样定理。具体的实验内容和实验步骤如下:
1、生成连续时间信号x(t)=-1000，绘制其在5ms到+5ms之间的波形，时间轴间隔为0.05ms。
2、编程实现x。(t)的傅立叶变换(即连续时间傅立叶变换)，并绘制其在-2KHz到+2KHz之间的幅度谱图，频率轴频率间隔设置为8Hz。
3、用采样频率f, = 5000Hz对x(t)=e-100进行理想采样，得到采样后离散时间信号x(n)，绘制出采样后的信号序列。
4、编程实现采样后离散时间信号x(n)的傅立叶变换(离散时间傅立叶变换)，并绘制其幅度谱图。
5、对采样前后的信号时域图形和频谱图进行分析，总结采样前后信号频谱之间的关系。
6、更改采样频率为f,=2000Hz和f,=1000Hz重复上述过程，对结果进行分析，并验证时域采样定理。

实验例程：

%连续时间信号生成
Dt=0.00005;t=-0.005:Dt:0.005;xa=exp(-1000*abs(t));
subplot(4,2,1);plot(t*1000,xa);xlabel('时间(毫秒)');ylabel('xa(t)');title('模拟信号');
%连续时间信号傅里叶变换
Wmax=2*pi*2000;K=500;k=0:1:K;W=k*Wmax/K;Xa=xa*exp(-j*t'*W)*Dt;Xa=real(Xa);W=[-fliplr(W),W(2:501)];Xa=[fliplr(Xa),Xa(2:501)];
subplot(4,2,2);plot(W/(2*pi*1000),Xa*1000);xlabel('频率(KHZ)');ylabel('Xa(jW)');title('连续时间傅里叶变换');
%1000HZ连续时间采样
fs=1000;Ts=1/fs;n1=-0.005/Ts:1:0.005/Ts;x1=exp(-1000*abs(n1*Ts));
subplot(4,2,3);stem(n1*Ts*1000,x1);ylabel('x1(n)');title('离散信号-fs=1000HZ');
%采样后傅里叶变换
K=500;k=0:1:K;w=pi*k/K;X1=x1*exp(-j*n1'*w);X1=real(X1);w=[-fliplr(w),w(2:K+1)];X1=[fliplr(X1),X1(2:K+1)];
subplot(4,2,4);plot(w/pi,X1);xlabel('频率(rad)');ylabel('X1(w)');title('离散傅里叶变换')
%2000HZ连续时间采样
fs=2000;Ts=1/fs;n1=-0.005/Ts:1:0.005/Ts;x1=exp(-1000*abs(n1*Ts));
subplot(4,2,5);stem(n1*Ts*1000,x1);ylabel('x1(n)');title('离散信号-fs=2000HZ');
%采样后傅里叶变换
K=500;k=0:1:K;w=pi*k/K;X1=x1*exp(-j*n1'*w);X1=real(X1);w=[-fliplr(w),w(2:K+1)];X1=[fliplr(X1),X1(2:K+1)];
subplot(4,2,6);plot(w/pi,X1);xlabel('频率(rad)');ylabel('X1(w)');title('离散傅里叶变换')
%5000HZ连续时间采样
fs=5000;Ts=1/fs;n1=-0.005/Ts:1:0.005/Ts;x1=exp(-1000*abs(n1*Ts));
subplot(4,2,7);stem(n1*Ts*1000,x1);ylabel('x1(n)');title('离散信号-fs=5000HZ');
%采样后傅里叶变换
K=500;k=0:1:K;w=pi*k/K;X1=x1*exp(-j*n1'*w);X1=real(X1);w=[-fliplr(w),w(2:K+1)];X1=[fliplr(X1),X1(2:K+1)];
subplot(4,2,8);plot(w/pi,X1);xlabel('频率(rad)');ylabel('X1(w)');title('离散傅里叶变换')

在这里插入图片描述

四、分析

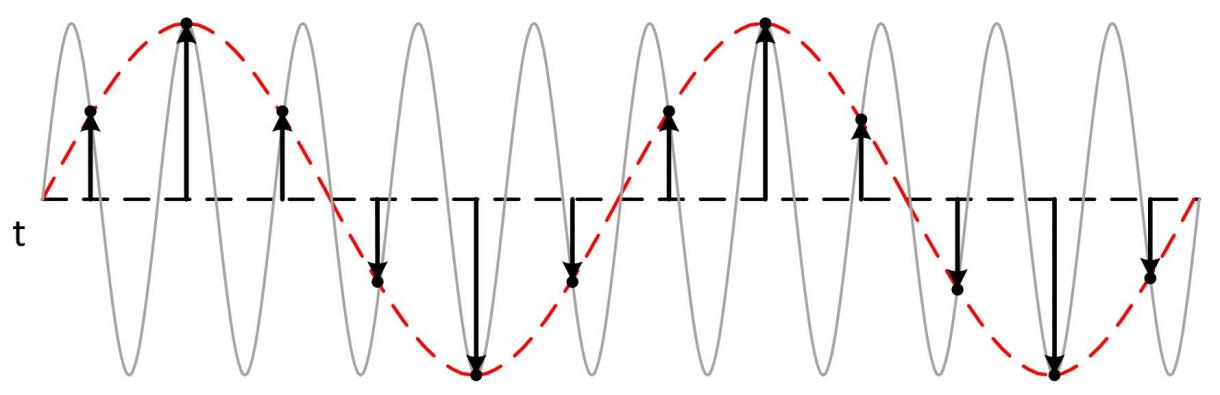
采样信号的频谱是原连续时间信号的频谱的周期性的复制（当然要保证采样满足奈奎斯特定理）。若采样周期为F，则采样后信号的频谱变成周期的了，周期为F，幅值变为原来的F倍，一个周期的形状和连续信号时的频谱一样。那么采样后离散信号的频谱应该[在满足采样定理]能反映出，原模拟信号的频谱，否则采样是没有意义的。采样后频谱是，原频谱的周期延拓，实际中需要将原来的高于有用频率的分量尽量滤除，增大采样频率来减少频谱的混叠。频带为F的连续信号f(t)可用一系列离散的采样值f(t1),f(t1±Δt)，f(t1±2Δt)，…来表示,只要这些采样点的时间间隔Δt≤1/(2F)，便可根据各采样值完全恢复原来的信号f(t)。这是时域采样定理的一种表述方式。时域采样定理的另一种表述方式是：当时间信号函数f(t)的最高频率分量为fM时,f(t)的值可由一系列采样间隔小于或等于1/(2fM)的采样值来确定,即采样点的重复频率f≥(2fM)。图为模拟信号和采样样本的示意图。时域采样定理是采样误差理论、随机变量采样理论和多变量采样理论的基础。