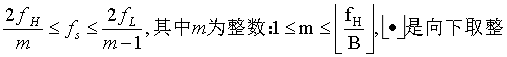1. 奈奎斯特采样定理是连接连续和离散的桥梁。现实世界中接触到的信号，比如电信号，光信号，声音信号等都是随时间连续变化的，称为连续信号。但对于计算机来说如要处理连续信号，这是无能为力的，必须要将连续信号转化为离散信号，这个过程就叫采样。采样后，计算机得到是离散的点，用这些离散的点代替连续的线必然有误差，那么怎样根据采样还原出原来的信号呢？奈奎斯特采样定理就出现了。奈奎斯特采样定理的内容是采样频率必须为大于等于2倍的最大频率分量，才能还原出原来的信号，它又叫低通采样定理。

        那么为什么采样频率大于等于最大频率分量2倍以上就能还原出信号呢？从时域上分析，采样频率大于它的两倍，相当于被采信号每个周期采样了两个点。最理想条件下，对于一个正（余）弦信号的曲线，两个点就能还原出原始信号，我们并不需要将曲线上面每一点都记录下来，只需要就一些特殊点就够了，比如相邻两个零点的位置（上图红色的两个点）或者相邻的波峰和波谷的位置（上图绿色的两个点），只要是按照正（余）弦信号的规则，就能够根据这些特殊点还原出正（余）弦信号，用香农信息论的观点来看就是这两个点已经包含了正（余）弦信号的信息熵，两个点足矣。理论上最理想条件上如下图：

        

        定量分析：上图所示正弦信号周期为1，两个采样点，无论是相邻的两个零点还是相邻的波峰与波谷位置的间隔都是0.5，因此，可知采样的周期为0.5，恰好为正弦信号周期的一半。从频谱来看，采样使频谱发生的周期性延拓，为了使延拓后的频谱不发生混叠，因此，采样周期必须为信号周期的2倍。

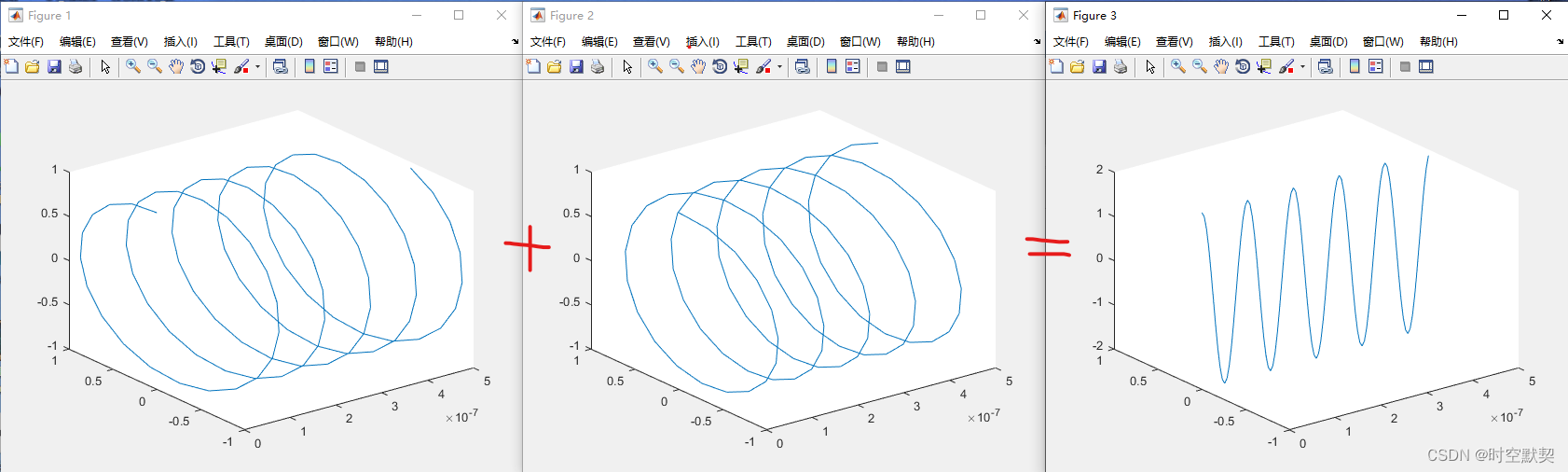
        同样频域上也能验证奈奎斯特采样定理，以频率f采样，相当于在频域以f为周期进行频谱的搬移。恢复出信号的条件：在频域上频谱不能混叠。在最理想条件上，采样频率必须大于等于它最高频率的两倍，这样频谱才不会混叠，下图能直观的展示：

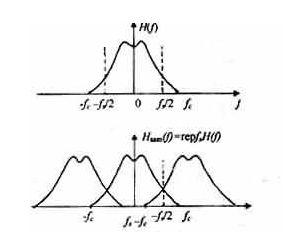
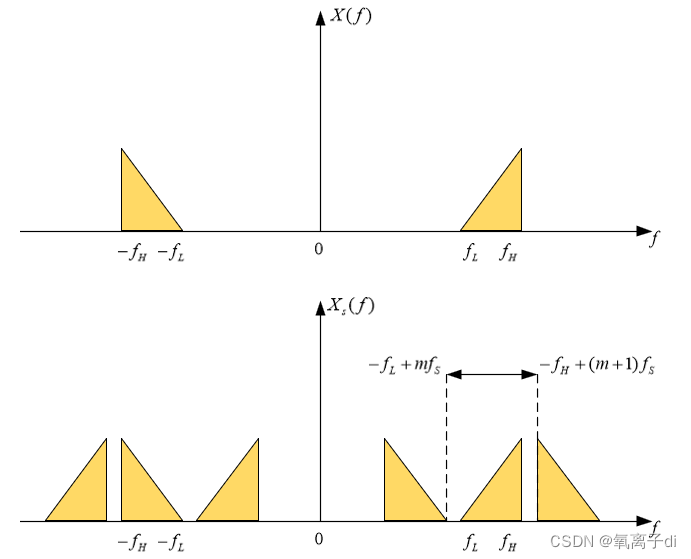
 2.奈奎斯特采样定理还有另一种表述形式，引申出带通采样定理。带通采样：对应带通信号，如果我们还是采用采样频率大于等于两倍的最大频率的策略，虽然这样采样后的信号的频谱仍是原信号频谱的周期延拓并不会出现混叠，理论上是可以再从采样信号中恢复出原信号的，但是这样做你会发现采样信号的频谱中有大量的空白，而带通抽样定理就是充分利用这些空白，通过数学计算得出合适的采用频率，在新的采样频率下采样可以使得采样后的信号的频谱中原来那些是空白的位置被放置了频率且没有混叠，这样不仅和低通采样定理一样没有信息的丢失，并且降低了对采样频率的要求，节省了资源。举个例子：设带通信号m(t),其频率限制在fL与fH之间，带宽为B=fH-fL，如果最小抽样速率fs=2fH/m,m是一个不超过fH/B的最大整数，那么m(t),可以完全由其抽样值确定。
对于单频信号时，其最低采样速率可以接近于0.因为信号带宽接近于0。