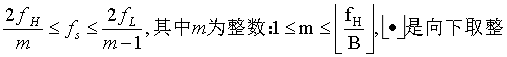数字信号处理:时域采样定理与频域采样定理
1.时域采样定理
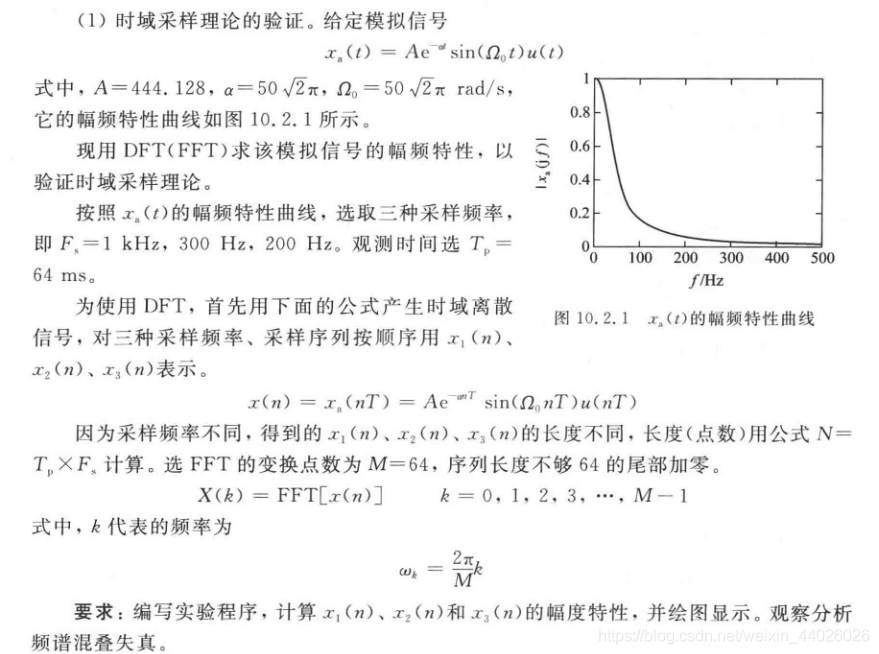
%初始参数
A=444.128;
alph=pi*50*2^0.5;
omega=pi*50*2^0.5;
M=64; %做64点fft变换
n=0:M-1;%采样频率fs为1000Hz
Fs1=1000;
T1=1/Fs1;
xn1=A*exp(-alph*n*T1).*sin(omega*n*T1); %对原函数的抽样取点
Xk1=fft(xn1,M); %fft变换后
Xk1=abs(Xk1); %取幅值
subplot(3,2,1);stem(n,xn1);
title('(a) Fs=1000Hz');xlabel('n');ylabel('xa(nT)');
subplot(3,2,2);plot(n,Xk1);
title('(b) Fs=1000Hz');xlabel('f/Hz');ylabel('幅度');%采样频率为300Hz
Fs2=300;
T2=1/Fs2;
xn2=A*exp(-alph*n*T2).*sin(omega*n*T2);
Xk2=fft(xn2,M);
Xk2=abs(Xk2);
subplot(3,2,3);stem(n,xn2);
title('(c) Fs=300Hz');xlabel('n');ylabel('xa(nT)');
subplot(3,2,4);plot(n,Xk2);
title('(d) Fs=300Hz');xlabel('f/Hz');ylabel('幅度');%采样频率为200Hz
Fs3=200;
T3=1/Fs3;
xn3=A*exp(-alph*n*T3).*sin(omega*n*T3);
Xk3=fft(xn3,M);
Xk3=abs(Xk3);
subplot(3,2,5);stem(n,xn3);
title('(e) Fs=200Hz');xlabel('n');ylabel('xa(nT)');
subplot(3,2,6);plot(n,Xk3);
title('(f) Fs=200Hz');xlabel('f/Hz');ylabel('幅度');

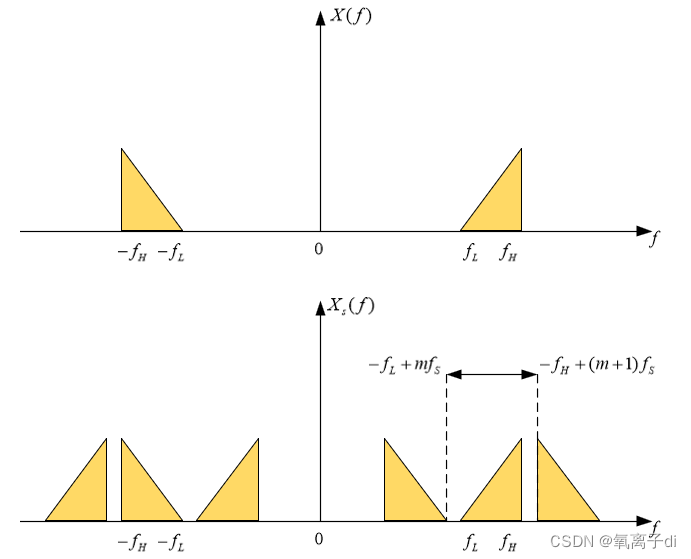
由结果图我们可以发现,当采样频率取1000Hz时,混叠还很小,而当采样频率取300Hz和200Hz时,混叠现象十分严重。所以我们可以得出,采样频率的取值Fs对于频谱是否重叠起着非常关键的作用。这样就验证了时域采样定理,采样频率 必须大于等于模拟信号最高频率的两倍以上,才能使采样信号的频谱不产生频谱混叠。
2.频域采样定理

M=27;N=32;
n=0:M;
%生成三角波序列x(n)
xa=0:floor(M/2);xb=ceil(M/2)-1:-1:0;
xn=[xa,xb];
%做fft变换
Xk=fft(xn,1024); %1024点fft用于近似序列FT[x(n)]
X32k=fft(xn,32);
x32n=ifft(X32k);
X16k=fft(xn,16);
x16n=ifft(X16k);
%作图
subplot(3,2,1);
k=0:1023;kk=2*k/1024;
plot(kk,abs(Xk));xlabel('w/\pi');ylabel('|X(e^j^\omega)|');
title('(a) FT[x(n)]');subplot(3,2,2);
stem(n,xn,'.'); %这样会变成实心点
xlabel('n');ylabel('x(n)');
title('(b) 三角波序列x(n)');subplot(3,2,3);
k=0:31;
stem(k,abs(X32k));xlabel('k');ylabel('|X_3_2(k)|');
title('(c) 32点频域采样');subplot(3,2,4);
stem(k,x32n);xlabel('n');ylabel('x_3_2(n)');
title('(d) 32点DFT');subplot(3,2,5);
k=0:15;
stem(k,abs(X16k));xlabel('k');ylabel('|X_1_6(k)|');
title('(e) 16点频域采样');subplot(3,2,6);
stem(k,x16n);xlabel('n');ylabel('x_1_6(n)');
axis([0,40,0,20]);%控制图像坐标范围
title('(f) 16点DFT');

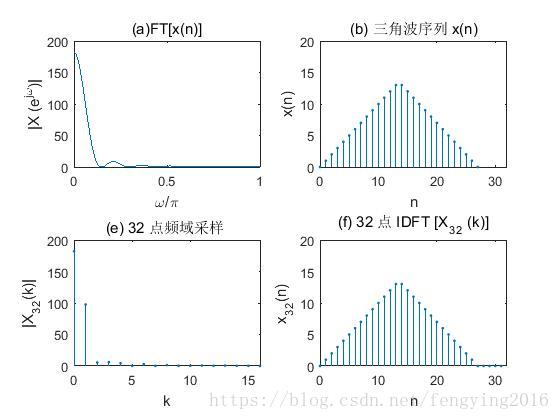
由上图(b)可知,三角波序列长度为26,即时域离散信号长度M为26。如图(f),当频域采样点数N(16)小于时域离散信号的长度M(26)时,将发生时域混叠失真。而如图(d),当频域采样点数N(32)大于时域离散信号的长度M(26)时,没有发生失真现象。由此验证了频域采样定理,即频域采样点数N必须大于时域离散信号的长度M(N>=M)。