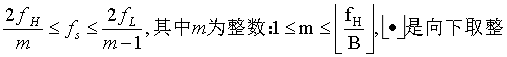一些闲话:
这是我本科生涯的最后一年了,过去三年毫无征兆地蒸发了一样,我的大四上有一门移动通信课,在实验课后我突发的迫切想要搭建一个完整的通信系统,所以我想趁着大四上最后一个月好好将我的知识进行总结,算是留给自己的一个纪念品。这是通信系统的第一站。
目录
一些闲话:
一、前言
二、联系实际
三、分析
四、数学过程
1.当 时:
2.当 时:
而 就被称为南奎斯特采样定律!
五、MATLAB 实现
一、前言
采样定理并不是复杂且难以理解的一个知识,但是它却是数字信号处理非常重要的一环,通过采样定理我们了解到,在理想状况下,满足什么条件的采样频率可以保证连续信号的离散处理能不失去原本的信息(也即能完好地将采样后的信号复原)。采样定理是美国电信工程师H.奈奎斯特在1928年提出的,要理解采样定理,只需要对连续时间傅里叶变换(CTFT:Continuous Time Fourier Transform)有足够的了解即可。想要加深对傅里叶变换的理解,可以看看这位Up主的视频。
纯干货数学推导_傅里叶级数与傅里叶变换_Part1_三角函数的正交性_哔哩哔哩_bilibili傅里叶级数,变换的数学基础。三角函数的正交性。******DR_CAN的论文预审/润色,留学文书,闪光点发掘以及科研咨询指导请参考:https://www.bilibili.com/read/cv3840089 https://www.bilibili.com/video/BV1Et411R78v?from=search&seid=10412896178040685619&spm_id_from=333.337.0.0本篇文章将从实际问题出发,引出采样,再分析怎么采样,最后通过数学推导得出采样定理。
https://www.bilibili.com/video/BV1Et411R78v?from=search&seid=10412896178040685619&spm_id_from=333.337.0.0本篇文章将从实际问题出发,引出采样,再分析怎么采样,最后通过数学推导得出采样定理。
二、联系实际
我们生活的空间中存在着极其多的信号,如果你细想,会发现很多东西在悄无声息地进行着。比如声信号,我们想要录下我们的歌声,并对其“充电”,使它如同被电鳗咬了一样,然后再放给别人听。我们是如何接收这些声信号,并将其放在电脑里进行一定的处理的呢?带着这个问题我们将进入这一章的内容。
或许在初中的时候,我们都学到过,声是一种波,波动传入麦克风里的某种传感器(Sensor)从而产生了连续的电信号,而这种连续的电信号,或者说模拟信号(Analogue Signal),是我们今天第一个主角。我们把它写作 。比如它长这样:

我们又知道,电脑里面处理的可不是这种模拟信号,而是一长串由0和1组成的比特流。比如它长这样: 000111010111000100101101
是什么过程让这两个看起来完全不是一个妈生的东西相互转换?答案是:采样(Sampling)和量化(Quantization)和编码(Coding)。本篇先讨论采样。
三、分析
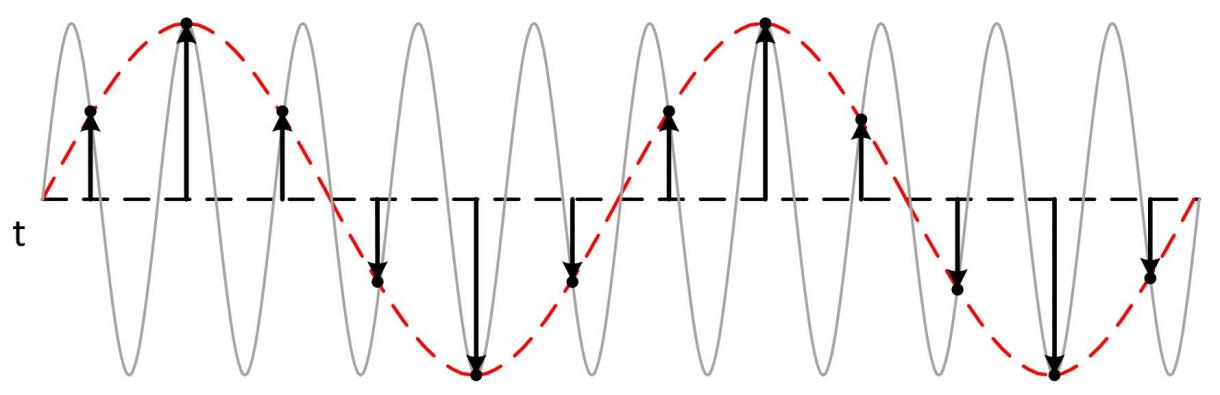
采样,顾名思义,采集样本,而对声信号也一样,我们无非就是想采集连续的电信号,让它能存在我们的设备里。你要知道一件事,我们存东西只能存在寄存器里,连续的信号可以说有无限个点,而寄存器是有限个的,所以我们必须得舍弃很多点,只隔一段时间采一个样本,隔一段时间再采一个样本。比如我们按Ts(采样间隔:Sampling Interval)采样,那么这时候它长这样:

经过保持(Hoding)它就长这样:

刚学到这里的朋友可以先不管这条往下看。看完再回来。提醒一下,实际中,S/H电路在很小的间隔
内跟踪模拟信号s(t),并且生成模拟信号在这个间隔内的平均值。所以由一个实际的S/H电路进行的平均运算等价于将连续时间信号通过一个频率响应为
的LTI离散时间系统。 具体可以看一本书第三章:Digital Signal Processing: A Computer-Based Approach. 但是如果跟踪周期
远小于采样周期Ts则上述影响可以忽略不计。
非常自然地,我们会想要尽可能地保留所有的信号点,所以理论上采样点越多越好。采样点越多,该声信号存储在设备中的信息就越多,我们将这个信号复原出来也就越逼近原信号。但是工程中总是要考虑成本问题,更高的采样频率意味着系统更高的复杂度。所以到底怎么样才能减小采样频率,又不失去信号的原有信息呢?答案是:保留频率信息即可。
在这里再推一篇文章,帮助你深入理解了Fourier Transform:
傅里叶分析之掐死教程(完整版)更新于2014.06.06 - 知乎作 者:韩 昊 知 乎:Heinrich 微 博:@花生油工人 知乎专栏:与时间无关的故事 谨以此文献给大连海事大学的吴楠老师,柳晓鸣老师,王新年老师以及张晶泊老师。 转载的同学请保留上面这句话,谢谢。如果还能保留文…![]() https://zhuanlan.zhihu.com/p/19763358
https://zhuanlan.zhihu.com/p/19763358
我的理解只有一句话,任何波形理论上都能通过足够充分的余弦波叠加而成,或者逼近。所以只需要足够的频率信息就能复原。
总结就是:采样只要保留足够的频率信息就能将原信号复原。
四、数学过程
根据上面的分析,一切需求变得明朗,又变成了数学问题。唉,工程师的生活就是那么枯燥无味。
设声信号:,对其采样其实就是拿很多个冲击函数和他相乘,它看起来是这样:

数学公式长这样:
所以推导过程如下:(不想打公式呜呜呜,字也写得丑呜呜呜)

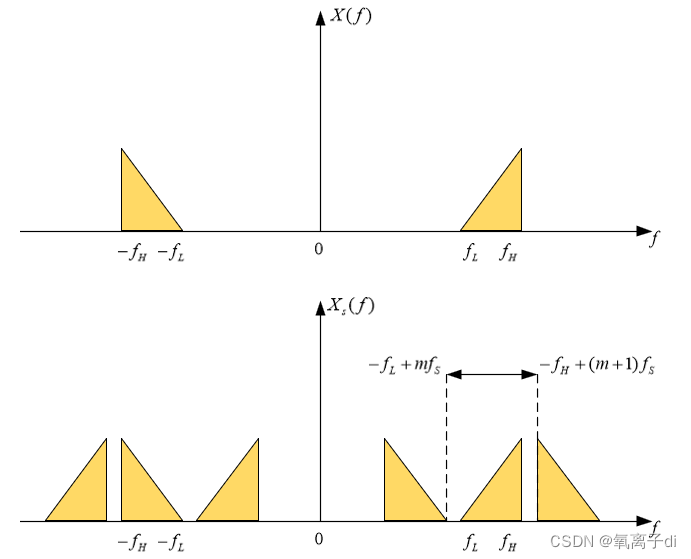
所以我们在公式上我们看到,时域的采样导致域的滑动叠加,假设
域的s(t)长这样:

注意!这里的频域应该是对称的,为什么? 因为语音信号是实信号,实信号的傅里叶变换是实偶奇虚的,也就是说,他的幅度响应(Magnitude Response)一定是对称的。推导如下:
所以滑动后有两种结果:
1.当  时:
时:

可以清晰看见,频域平移后无混叠,频率信息保存完好,通过低通滤波器(Low Pass Filter)即可漂亮地得到频域信息,然后通过内插(Interpolation)复原。 (内插以后再讲)
2.当 时:
时:

可以清晰地看见,频域平移后混叠,频率信息受到迫害,失真,导致无法通过滤波然后复原原本信号。
而  就被称为南奎斯特采样定律!
就被称为南奎斯特采样定律!
ok,让我把这篇文章封面送给南奎斯特!
五、MATLAB 实现
后续再填