频域采样定理

1、频域采样定理的主要内容是:
(a)对信号$x(n)$的频谱函数 $X (e^{jw} )$ 在$[0,2\pi )$上等间隔采样 N点，得到：

$$X_N(k)=X(e^{jw})|_{w=2\pi k/N}　，　　k=0,1,2,...,N-1$$

则N点IDFT$[X_N(k)]$得到的序列就是原序列$x(n)$以N为周期延拓后的主值区序列，公式为：

$$x_{N}(n)=IDFT[X_N(k)]_N=[\sum_{i=-\propto }^{\propto }x(n+iN)]R_N(n)$$

(b)频域采样点数N必须大于等于时域离散信号的长度M (即$N\geqslant M$)，才能使时域不产生混叠，且N点$IDFT[X_N(k)]$得到的序列$x_N(n)$ 就是原序列$x(n)$，即 $x_N(n)=x(n)$ 。如果$N > M$，$x_N(n)$比原序列多$N -M$个零点；如果$N < M$，则$x_N(n)=IDFT[X_N(k)]$发生了时域混叠失真，而且$x_N(n)$的长度也比 $x(n)$ 的长度短。
2、应用
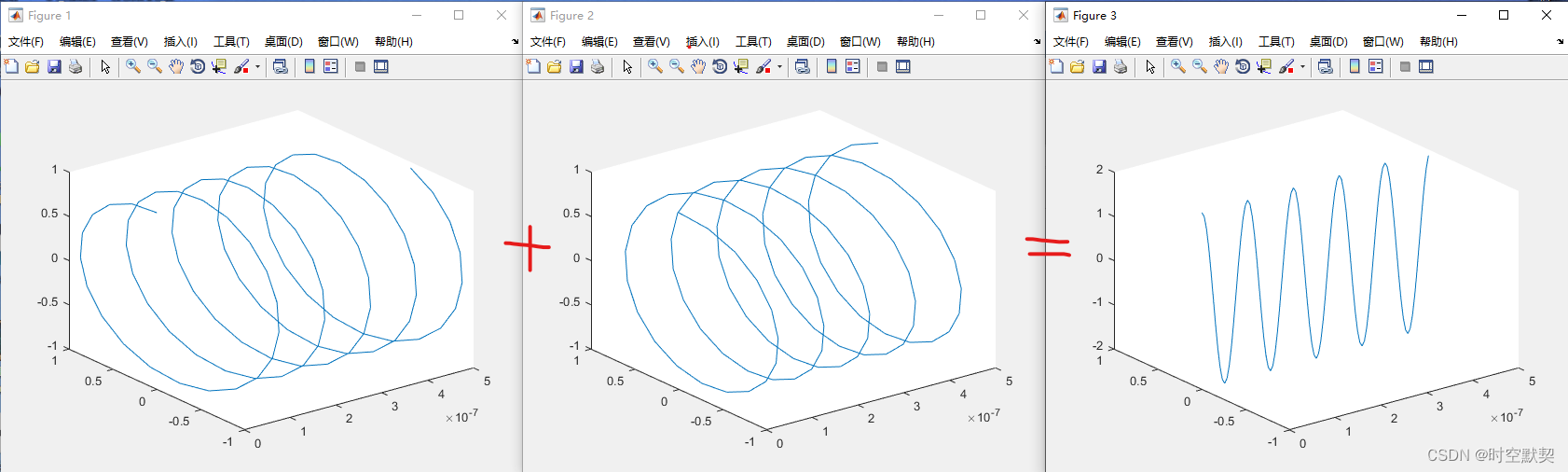
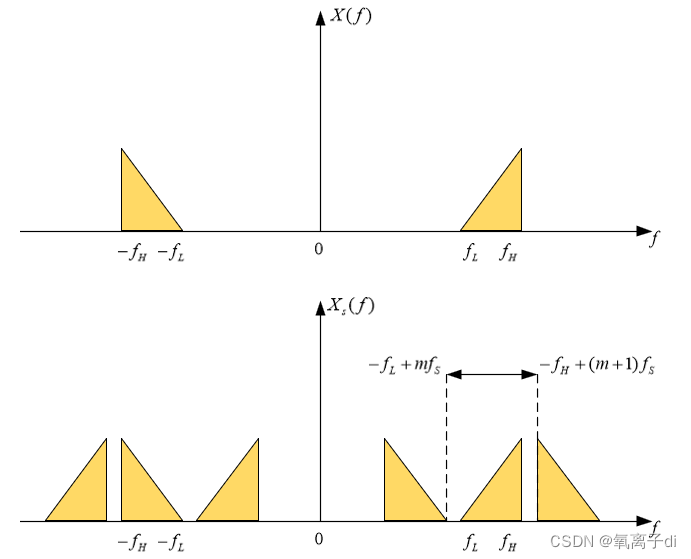
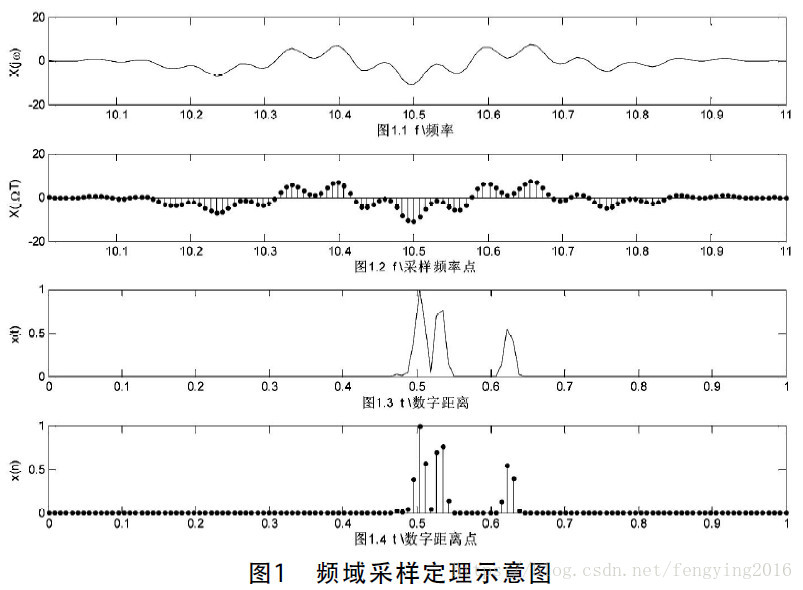
　　典型的频域采样定理应用是雷达目标距离像的提取。当雷达用不同的频率照射目标时，将会得到对应不同频率的反射回波的幅值。图1是频域采样定理的示意图。其中，图1.1为频域连续信号、图1.2为频域采样得到的数字信号、图1.3为连续傅立叶变换、图1.4为离散傅立叶变换。常见的雷达目标识别信号处理过程基本上都是基于频域采样定理展开的。
　　
3、频域采样定理的matlab验证
给定信号如下：

$$\left\{\begin{matrix} n+1，0\leqslant n\leqslant 13 \\ 27-n，14\leqslant n\leqslant 26 \\ 0，　　　其他　　　 \end{matrix}\right.$$
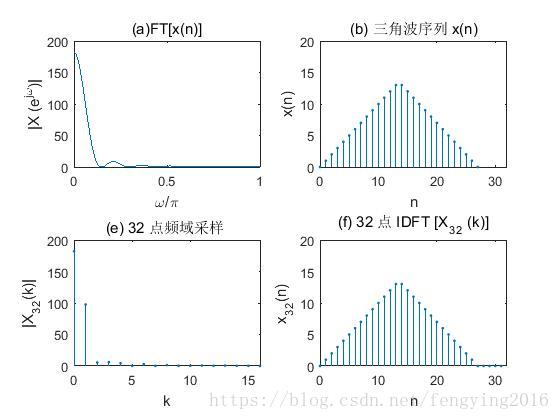
对频谱函数 $X（e^{jw}）=FT[x（n）]$在区间 $[0，2\pi]$上等间隔32 点采样，得到 $X_{32}（k）$。再对 $X_{32}（k）$进行32 点IFFT。分别画出 $X（e^{jw}）、X_{32}（k）$的幅度谱，并绘图显示 $x（n）、X_{32}（n）$的波形。

clear all;
M=27;N=32;n=0:M;%产生M长三角波序列 x(n)
xa=0:floor(M/2); 
xb= ceil(M/2)-1:-1:0; 
xn=[xa,xb];
Xk=fft(xn,1024); %1024 点FFT[x(n)],用于近似序列x(n)的TF
X32k=fft(xn,32) ;%32 点FFT[x(n)]
x32n=ifft(X32k); %32 点IFFT[X32(k)]得到x32(n)
subplot(2,2,2);stem(n,xn,'.');box on
title('(b) 三角波序列x(n)');xlabel('n');ylabel('x(n)');axis([0,32,0,20])k=0:1023;wk=2*k/1024; %
subplot(2,2,1);plot(wk,abs(Xk));title('(a)FT[x(n)]');
xlabel ('\omega/\pi');ylabel ('|X (e^j^\omega)|');axis([0,1,0,200])k=0:N-1;
subplot(2,2,3);stem(k,abs(X32k),'.');box on
title('(e) 32 点频域采样');xlabel('k');ylabel('|X_3_2(k)|');axis([0,16,0,200])n1=0:N-1;
subplot(2,2,4);stem(n1,x32n,'.');box on
title ('(f) 32 点 IDFT [X_3_2 (k)]');xlabel('n');ylabel('x_3_2(n)');axis([0,32,0,20])