文章目录
- 循环卷积
- 循环矩阵(Circulant Matrices)
- 循环矩阵与循环卷积的关系
- 线性卷积
循环卷积
循环矩阵(Circulant Matrices)
C = [ c 0 c 1 ⋯ c N − 1 c N − 1 c 0 ⋱ ⋮ ⋮ ⋱ ⋱ c 1 c 1 ⋯ c N − 1 c 0 ] ∈ R N × N (1) \boldsymbol{C}=\left[ \begin{matrix} c_0& c_1& \cdots& c_{N-1}\\ c_{N-1}& c_0& \ddots& \vdots\\ \vdots& \ddots& \ddots& c_1\\ c_1& \cdots& c_{N-1}& c_0\\ \end{matrix} \right] \in \mathbb R^{N \times N} \tag{1} C=⎣⎢⎢⎢⎢⎡c0cN−1⋮c1c1c0⋱⋯⋯⋱⋱cN−1cN−1⋮c1c0⎦⎥⎥⎥⎥⎤∈RN×N(1)
任意循环矩阵 C 1 , C 2 \boldsymbol C_1, \boldsymbol C_2 C1,C2, C 1 C 2 = C 2 C 1 \boldsymbol C_1 \boldsymbol C_2 = \boldsymbol C_2 \boldsymbol C_1 C1C2=C2C1也是循环阵(因此循环矩阵必然也是normal矩阵,因为 C C T = C T C \boldsymbol C \boldsymbol C^T= \boldsymbol C^T \boldsymbol C CCT=CTC)。循环阵可以表示为多项式形式:
C = c 0 I + c 1 P + ⋯ + c N − 1 P N − 1 (2) \boldsymbol C = c_0 \boldsymbol I + c_1 \boldsymbol P + \cdots + c_{N-1} \boldsymbol P^{N-1} \tag{2} C=c0I+c1P+⋯+cN−1PN−1(2)
其中 P \boldsymbol P P为循环移位矩阵(Circlic Shift Matrix) ,这里我们考虑up cyclic shit matrix (down cyclic shift matrix 类似),以 N = 4 N=4 N=4为例
P = [ 0 1 0 0 0 0 1 0 0 0 0 1 1 0 0 0 ] (3) \boldsymbol{P}=\left[ \begin{matrix} 0& 1& 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1\\ 1& 0& 0& 0\\ \end{matrix} \right] \tag{3} P=⎣⎢⎢⎡0001100001000010⎦⎥⎥⎤(3)
其循环移位过程可以从下式看出
P [ x 1 x 2 x 3 x 4 ] = [ 0 1 0 0 0 0 1 0 0 0 0 1 1 0 0 0 ] [ x 1 x 2 x 3 x 4 ] = [ x 2 x 3 x 4 x 1 ] (4) \boldsymbol P \left[ \begin{array}{c} x_1\\ x_2\\ x_3\\ x_4\\ \end{array} \right] = \left[ \begin{matrix} 0& 1& 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1\\ 1& 0& 0& 0\\ \end{matrix} \right] \left[ \begin{array}{c} x_1\\ x_2\\ x_3\\ x_4\\ \end{array} \right] = \left[ \begin{array}{c} x_2\\ x_3\\ x_4\\ x_1\\ \end{array} \right] \tag{4} P⎣⎢⎢⎡x1x2x3x4⎦⎥⎥⎤=⎣⎢⎢⎡0001100001000010⎦⎥⎥⎤⎣⎢⎢⎡x1x2x3x4⎦⎥⎥⎤=⎣⎢⎢⎡x2x3x4x1⎦⎥⎥⎤(4)
因为 P \boldsymbol P P是循环移位矩阵,所以
P N = I (5) \boldsymbol P^N = \boldsymbol I \tag{5} PN=I(5)
这里 N = 4 N=4 N=4。
根据式(2),不难得出, C \boldsymbol C C的特征向量与 P \boldsymbol P P的特征向量等价,因此我们主要分析 P \boldsymbol P P的谱特性。
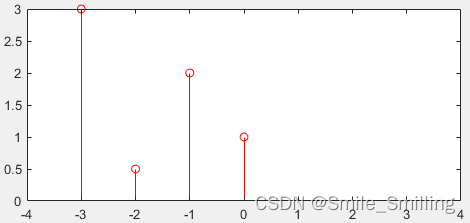
det ( P − λ I ) = det ( [ − λ 1 0 0 0 − λ 1 0 0 0 − λ 1 1 0 0 − λ ] ) = λ 4 − 1 = 0 ⇒ λ = 1 , − 1 , i , − i (5) \begin{aligned} \text{det} \left ( \boldsymbol P - \lambda \boldsymbol I \right ) &= \text{det} \left ( \left[ \begin{matrix} -\lambda& 1& 0& 0\\ 0& -\lambda& 1& 0\\ 0& 0& -\lambda& 1\\ 1& 0& 0& -\lambda\\ \end{matrix} \right] \right ) \\ & = \lambda^4 - 1 \\ & = 0 \\ \Rightarrow \lambda &= 1, -1, i, -i \end{aligned} \tag{5} det(P−λI)⇒λ=det⎝⎜⎜⎛⎣⎢⎢⎡−λ0011−λ0001−λ0001−λ⎦⎥⎥⎤⎠⎟⎟⎞=λ4−1=0=1,−1,i,−i(5)
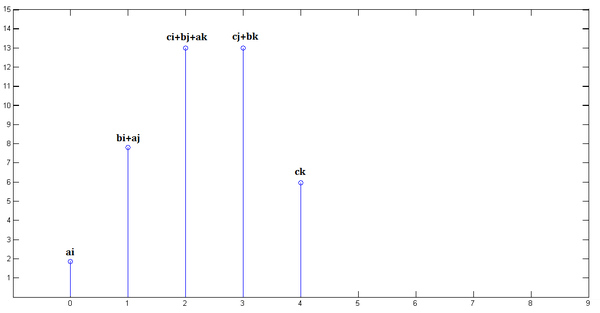
其特征值如下图所示
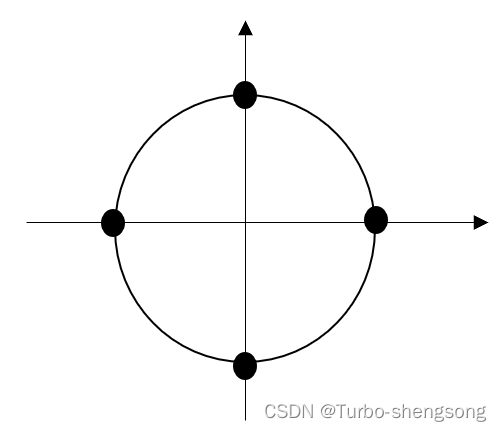
所对应的特征向量为
λ = 1 , [ 1 1 1 1 ] ; λ = − 1 , [ 1 − 1 1 − 1 ] ; λ = i , [ 1 i i 2 i 3 ] ; λ = − i , [ 1 − i ( − i ) 2 ( − i ) 3 ] (6) \lambda =1,\left[ \begin{array}{c} 1\\ 1\\ 1\\ 1\\ \end{array} \right] ; \lambda =-1,\left[ \begin{array}{c} 1\\ -1\\ 1\\ -1\\ \end{array} \right] ; \lambda =i,\left[ \begin{array}{c} 1\\ i\\ i^2\\ i^3\\ \end{array} \right] ; \lambda =-i,\left[ \begin{array}{c} 1\\ -i\\ \left( -i \right) ^2\\ \left( -i \right) ^3\\ \end{array} \right] \,\, \tag{6} λ=1,⎣⎢⎢⎡1111⎦⎥⎥⎤;λ=−1,⎣⎢⎢⎡1−11−1⎦⎥⎥⎤;λ=i,⎣⎢⎢⎡1ii2i3⎦⎥⎥⎤;λ=−i,⎣⎢⎢⎡1−i(−i)2(−i)3⎦⎥⎥⎤(6)
令
F = 1 2 [ 1 1 1 1 1 − 1 1 − 1 1 i i 2 i 3 1 − i ( − i ) 2 ( − i ) 3 ] (7) \boldsymbol{F}=\frac{1}{2} \left[ \begin{matrix} \begin{array}{c} 1\\ 1\\ 1\\ 1\\ \end{array}& \begin{array}{c} 1\\ -1\\ 1\\ -1\\ \end{array}& \begin{array}{c} 1\\ i\\ i^2\\ i^3\\ \end{array}& \begin{array}{c} 1\\ -i\\ \left( -i \right) ^2\\ \left( -i \right) ^3\\ \end{array}\\ \end{matrix} \right] \tag{7} F=21⎣⎢⎢⎡11111−11−11ii2i31−i(−i)2(−i)3⎦⎥⎥⎤(7)
对应的特征分解为
P = F [ 1 0 0 0 0 − 1 0 0 0 0 i 0 0 0 0 − i ] F H = F Λ F H (8) \begin{aligned} \boldsymbol P &= \boldsymbol F \left[ \begin{matrix} 1& 0& 0& 0\\ 0& -1& 0& 0\\ 0& 0& i& 0\\ 0& 0& 0& -i\\ \end{matrix} \right] \boldsymbol F^H \\ & = \boldsymbol F \boldsymbol \Lambda \boldsymbol F^H \end{aligned} \tag{8} P=F⎣⎢⎢⎡10000−10000i0000−i⎦⎥⎥⎤FH=FΛFH(8)
因此循环矩阵 C \boldsymbol C C的特征分解可以写为,
C = F ( c 0 I + c 1 Λ + c N − 1 Λ N − 1 ) F H (9 ) \boldsymbol C = \boldsymbol F \left ( c_0 \boldsymbol I + c_1 \boldsymbol \Lambda + c_{N-1} \boldsymbol \Lambda^{N-1} \right ) \boldsymbol F^H \tag{9 } C=F(c0I+c1Λ+cN−1ΛN−1)FH(9 )
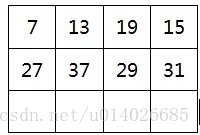
为了更好地理解,当 N = 8 N=8 N=8时,其特征值可以用下图表示
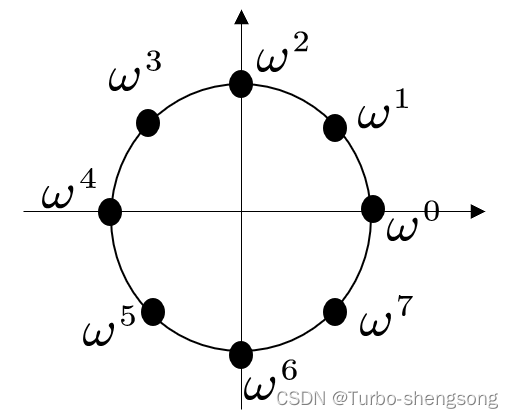
其中
ω = e 2 π i N , N = 8 (10) \omega = e^{\frac{2 \pi i}{N}} , \ \ N = 8 \tag{10} ω=eN2πi, N=8(10)
特征矩阵
F 8 = 1 8 [ 1 1 1 ⋯ 1 1 ω 1 ω 2 ⋯ ω 7 1 ω 2 ω 4 ⋯ ω 14 1 1 1 1 1 ω 3 ω 4 ω 5 ω 6 ω 7 ω 6 ω 8 ω 10 ω 12 ω 14 ⋯ ω 21 ⋯ ω 28 ⋯ ω 35 ⋯ ω 42 ⋯ ω 49 ] (11) \boldsymbol F_8 = \frac{1}{\sqrt 8} \left[ \begin{matrix} 1& 1& 1& \begin{matrix} \cdots& 1\\ \end{matrix}\\ 1& \omega ^1& \omega ^2& \begin{matrix} \cdots& \omega ^7\\ \end{matrix}\\ 1& \omega ^2& \omega ^4& \begin{matrix} \cdots& \omega ^{14}\\ \end{matrix}\\ \begin{array}{c} 1\\ 1\\ 1\\ \begin{array}{c} 1\\ 1\\ \end{array}\\ \end{array}& \begin{array}{c} \omega ^3\\ \omega ^4\\ \omega ^5\\ \begin{array}{c} \omega ^6\\ \omega ^7\\ \end{array}\\ \end{array}& \begin{array}{c} \omega ^6\\ \omega ^8\\ \omega ^{10}\\ \begin{array}{c} \omega ^{12}\\ \omega ^{14}\\ \end{array}\\ \end{array}& \begin{array}{c} \begin{matrix} \cdots& \omega ^{21}\\ \end{matrix}\\ \begin{matrix} \cdots& \omega ^{28}\\ \end{matrix}\\ \begin{matrix} \cdots& \omega ^{35}\\ \end{matrix}\\ \begin{array}{c} \begin{matrix} \cdots& \omega ^{42}\\ \end{matrix}\\ \begin{matrix} \cdots& \omega ^{49}\\ \end{matrix}\\ \end{array}\\ \end{array}\\ \end{matrix} \right] \tag{11} F8=81⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎡111111111ω1ω2ω3ω4ω5ω6ω71ω2ω4ω6ω8ω10ω12ω14⋯1⋯ω7⋯ω14⋯ω21⋯ω28⋯ω35⋯ω42⋯ω49⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎤(11)
一般地, F N \boldsymbol F_N FN中的第 ( k , n ) (k,n) (k,n)个元素为:
F N ( k , n ) = 1 N exp ( i 2 π k n N ) , 0 ≤ k , n ≤ N − 1 (12) \boldsymbol F_N (k,n) = \frac{1}{N}\exp (\frac{i 2 \pi k n}{N}) , \ \ 0 \leq k, n \leq N-1 \tag{12} FN(k,n)=N1exp(Ni2πkn), 0≤k,n≤N−1(12)
小结:循环矩阵 C \boldsymbol C C与循环移位矩阵 P \boldsymbol P P有密切的关系,尤其是谱空间意义上。一般地,循环矩阵 C \boldsymbol C C都可以被谱分解为
C = F D F H (13) \boldsymbol C = \boldsymbol F \boldsymbol D \boldsymbol F^H \tag{13} C=FDFH(13)
其中 F \boldsymbol F F为DFT矩阵, D \boldsymbol D D为对角阵,且多数情况下都是复数。
循环矩阵与循环卷积的关系
令
c T = [ c 0 , c 1 , ⋯ , c N − 1 ] ∈ R 1 × N v T = [ v 0 , v 1 , ⋯ , v N − 1 ] ∈ R 1 × N \boldsymbol c^T = [c_0, c_1, \cdots, c_{N-1}] \in \mathbb R^{1 \times N} \\ \boldsymbol v^T = [v_0, v_1, \cdots, v_{N-1}] \in \mathbb R^{1 \times N} cT=[c0,c1,⋯,cN−1]∈R1×NvT=[v0,v1,⋯,vN−1]∈R1×N
那么 c T \boldsymbol c^T cT 和 v T \boldsymbol v^T vT 的循环卷积为
c T ⊗ v T = v T [ c 0 c 1 ⋯ c N − 1 c N − 1 c 0 ⋱ ⋮ ⋮ ⋱ ⋱ c 1 c 1 ⋯ c N − 1 c 0 ] = c T [ v 0 v 1 ⋯ v N − 1 v N − 1 v 0 ⋱ ⋮ ⋮ ⋱ ⋱ v 1 v 1 ⋯ v N − 1 v 0 ] (14) \begin{aligned} & \boldsymbol c^T \otimes \boldsymbol v^T \\ & = \boldsymbol v^T \left[ \begin{matrix} c_0& c_1& \cdots& c_{N-1}\\ c_{N-1}& c_0& \ddots& \vdots\\ \vdots& \ddots& \ddots& c_1\\ c_1& \cdots& c_{N-1}& c_0\\ \end{matrix} \right] \\ & = \boldsymbol c^T \left[ \begin{matrix} v_0& v_1& \cdots& v_{N-1}\\ v_{N-1}& v_0& \ddots& \vdots\\ \vdots& \ddots& \ddots& v_1\\ v_1& \cdots& v_{N-1}& v_0\\ \end{matrix} \right] \end{aligned} \tag{14} cT⊗vT=vT⎣⎢⎢⎢⎢⎡c0cN−1⋮c1c1c0⋱⋯⋯⋱⋱cN−1cN−1⋮c1c0⎦⎥⎥⎥⎥⎤=cT⎣⎢⎢⎢⎢⎡v0vN−1⋮v1v1v0⋱⋯⋯⋱⋱vN−1vN−1⋮v1v0⎦⎥⎥⎥⎥⎤(14)
举例:令 c T = [ 3 , 1 , 2 ] \boldsymbol c^T=[3,1,2] cT=[3,1,2], v T = [ 4 , 6 , 1 ] \boldsymbol v^T=[4,6,1] vT=[4,6,1],那么
c T ⊗ v T = [ 3 , 1 , 2 ] ⊗ [ 4 , 6 , 1 ] = [ 4 , 6 , 1 ] [ 3 1 2 2 3 1 1 2 3 ] = [ 3 , 1 , 2 ] [ 4 6 1 1 4 6 6 1 4 ] = [ 25 , 14 , 17 ] \begin{aligned} \boldsymbol c^T \otimes \boldsymbol v^T &= [3,1,2] \otimes [4,6,1] \\ & = [4,6,1] \left[ \begin{matrix} 3& 1& 2\\ 2& 3& 1\\ 1& 2& 3\\ \end{matrix} \right] \\ & = [3,1,2] \left[ \begin{matrix} 4& 6& 1\\ 1& 4& 6\\ 6& 1& 4\\ \end{matrix} \right] \\ &= [25, 14, 17] \end{aligned} cT⊗vT=[3,1,2]⊗[4,6,1]=[4,6,1]⎣⎡321132213⎦⎤=[3,1,2]⎣⎡416641164⎦⎤=[25,14,17]
除此之外,我们还可以使用多项式来求解
( 3 I + P + 2 P 2 ) ( 4 I + 6 P + P 2 ) = 12 I + 22 P + 17 P 2 + 13 P 3 + 2 P 4 = 25 + 24 P + 17 P 2 \begin{aligned} &(3\boldsymbol I+\boldsymbol P + 2 \boldsymbol P^2)(4 \boldsymbol I+6\boldsymbol P+\boldsymbol P^2)\\ &= 12 \boldsymbol I + 22 \boldsymbol P + 17 \boldsymbol P^2 + 13 \boldsymbol P^3 + 2 \boldsymbol P^4 \\ & = 25 + 24 \boldsymbol P + 17 \boldsymbol P^2 \end{aligned} (3I+P+2P2)(4I+6P+P2)=12I+22P+17P2+13P3+2P4=25+24P+17P2
因为 P N = P \boldsymbol P^N = \boldsymbol P PN=P。
线性卷积
我们以一个线性时不变系统来说明:
r [ m ] = ∑ l = 1 L h l x [ m − l ] r[m] = \sum_{l=1}^L h_l x[m - l] r[m]=l=1∑Lhlx[m−l]
因为线性卷积较为常见,我们不做过多分析,直接给出矩阵意义下的线性卷积,令 h T = [ 4 , 6 , 1 ] \boldsymbol h^T = [4,6,1] hT=[4,6,1], x T = [ 3 , 1 , 2 ] \boldsymbol x^T = [3,1,2] xT=[3,1,2],那么
r T = h T ∗ x T = [ 4 , 6 , 1 ] [ 3 1 2 0 0 0 3 1 2 0 0 0 3 1 2 ] = [ 12 , 22 , 17 , 13 , 2 ] \begin{aligned} \boldsymbol r^T &= \boldsymbol h^T * \boldsymbol x^T \\ &= [4,6,1] \left[ \begin{matrix} 3& 1& \begin{matrix} 2& 0& 0\\ \end{matrix}\\ 0& 3& \begin{matrix} 1& 2& 0\\ \end{matrix}\\ 0& 0& \begin{matrix} 3& 1& 2\\ \end{matrix}\\ \end{matrix} \right] \\ & = [12,22,17,13,2] \end{aligned} rT=hT∗xT=[4,6,1]⎣⎡300130200120312⎦⎤=[12,22,17,13,2]