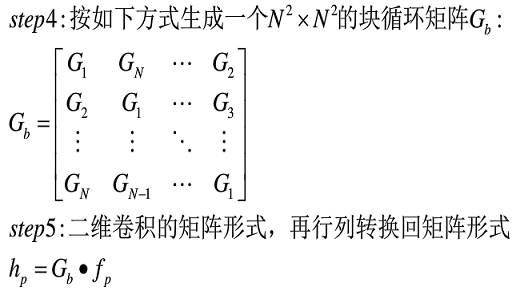
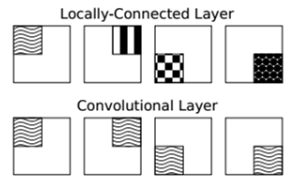
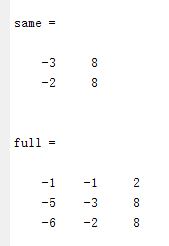为了验证后续矩阵卷积转化为矩阵相乘，这里给出的conv2的实例描述： 

        假设矩阵A（4*3）、B（2*3）如下：

               

       首先，B需要旋转180，

      命令旋转2次90即可：

      B = rot90(rot90(B));或者B = rot90(h,2);  结果为：

      

      其次：命令conv2函数：

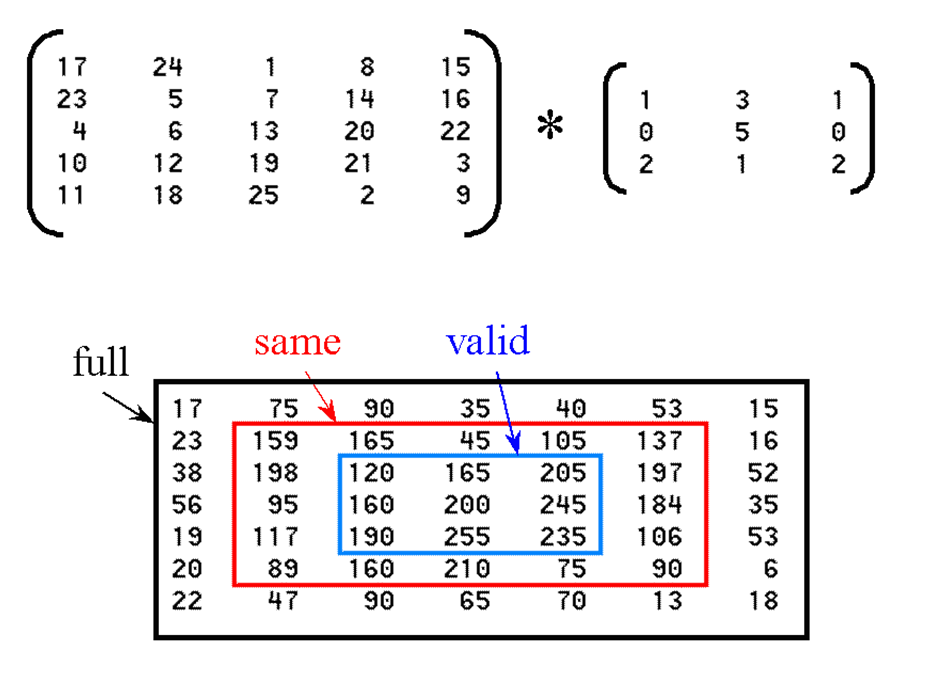
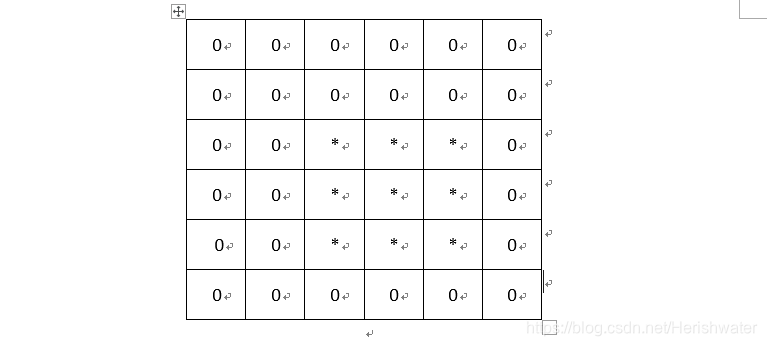
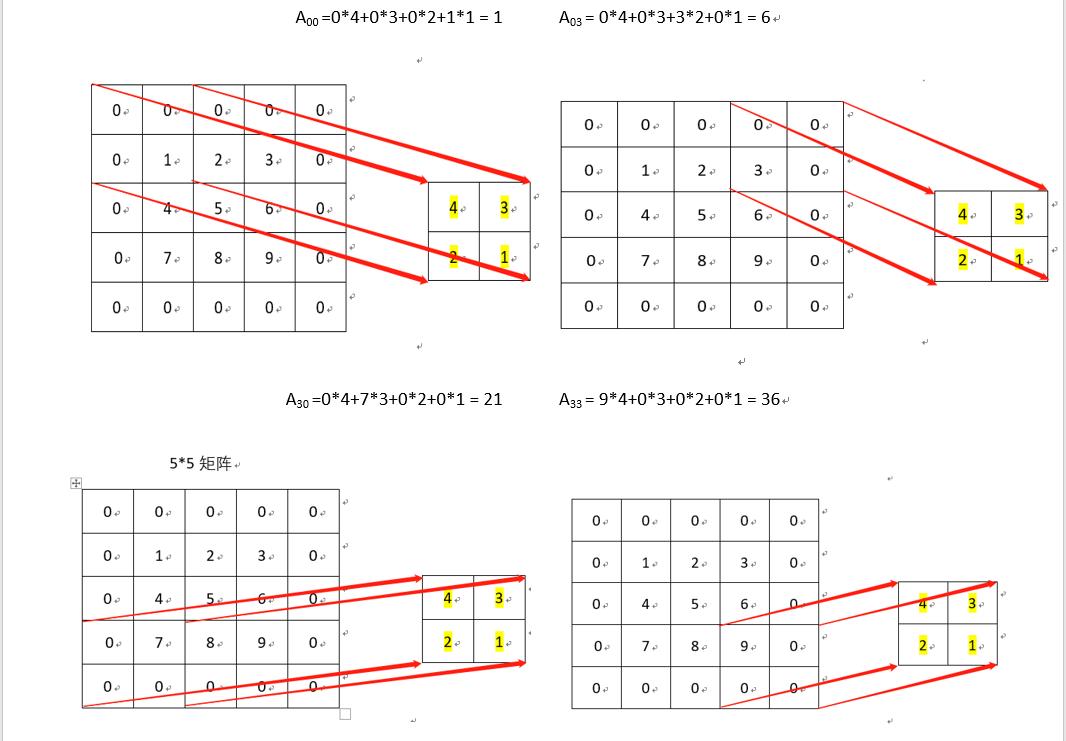
      C = conv2(A,B，‘shape’),该函数的具体操作图示：

                            

       依次计算直至结束，结果数据为：

    

         shape的取值有三种，full代表返回卷积以后的全部数据，size为(mA+mB-1,nA+nB-1)的数据；same代表返回卷积以后的原图size (mA,nA)的部分数据；valid返回size为(mA-mB+1,nA-nB+1)的数据，指的是模板元素全部参加运算的结果数据，即源图像和模板的交集为模板。
 

---

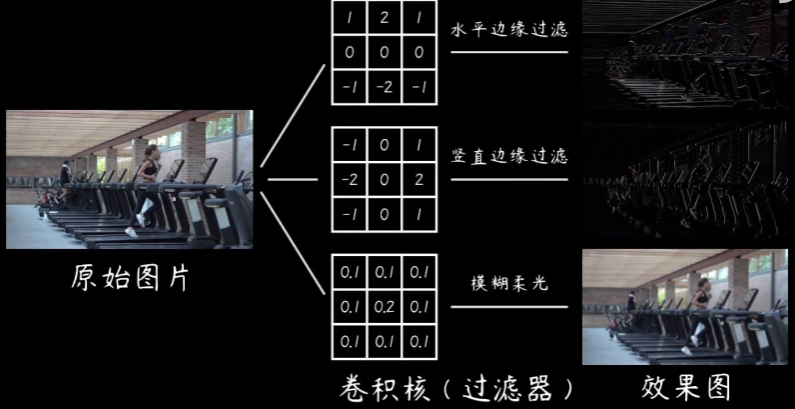
在图像处理的过程中，经常会看到矩阵卷积的概念，比如说用一个模板去和一张图片进行卷积，因此很有必要了解矩阵卷积到了做了什么，具体又是怎么计算的。 
在matlab中有conv2函数对矩阵进行卷积运算，其中有一个shape参数，取值具体有三种:

 -full  - (default) returns the full 2-D convolution,-'same'  - returns the central part of the convolutionthat is the same size as A.-'valid' - returns only those parts of the convolutionthat are computed without the zero-padded edges.size(C) = max([ma-max(0,mb-1),na-max(0,nb-1)],0).

用一幅图可以很好的理解这三个参数代码的具体含义： 

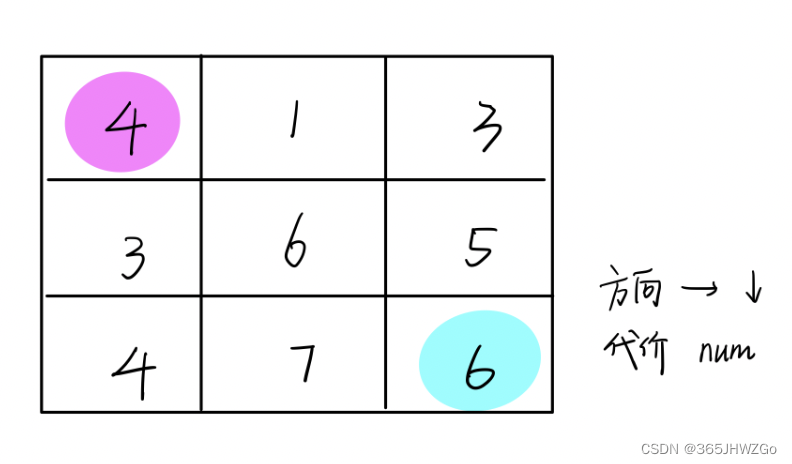
矩阵卷积计算方法

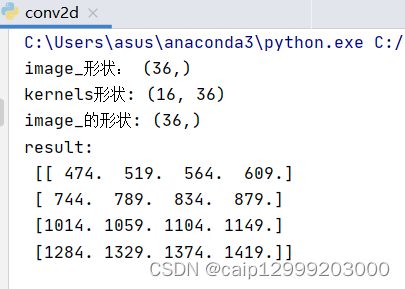
举一个简单的例子， 

matlab 的计算结果如下：