卷积码

  $(n,k,N)$卷积码是将每$k$个信息比特作为一组，编码成$n$个编码比特输出。$N$为编码的约束长度，表示编码过程中有N组信息比特相互约束。卷积码的编码器具有记忆性，针对每组信息比特（$k$个比特）输入，有n个编码比特输出，编码比特不仅与当前输入的$k$个信息比特有关系，还与前$N-1$个$k$位输入信息比特有关。编码效率为${\eta }_c=\frac{k}{n}$。${\eta }_c$和$N$是衡量卷积码性能的两个重要参数。
（关于$N$的含义，我在不同地方看到的不一样，有的说是编码过程中有$N$组信息比特相互约束，还有说是编码过程中有$N+1$组信息比特相互约束，本文我采用前者。）

卷积码编码器

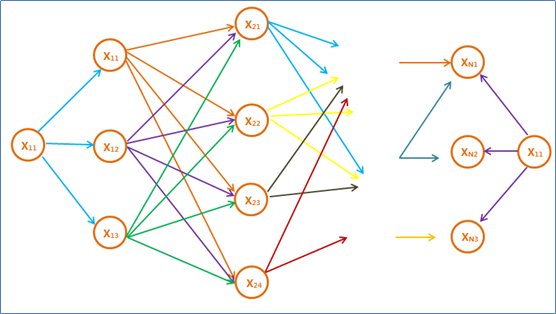
  $(n,k,N)$卷积码的编码器由$N$组$k$级输入移位寄存器（$N\times k$位寄存器）、$n$级输出移位寄存器和$n$个模2和加法器构成，每个输出移位寄存器有一个模2和加法器与其对应，每个模2和加法器输入端的数目不一定相同。下图为$(n,k,N)$卷积码编码器原理图。

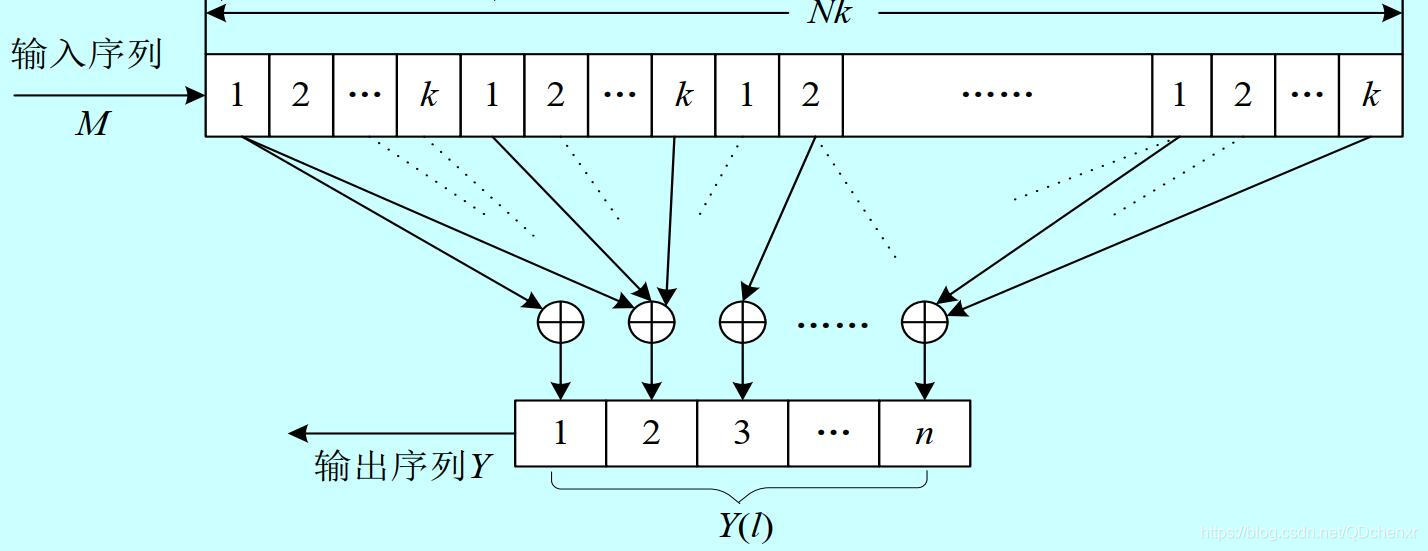
  卷积码的生成矩阵就是在描述$N\times k$位输入移位寄存器的每一位与每个模2和加法器的连接关系。

卷积码生成矩阵

  教材上是按照先子生成矩阵、生成矩阵后生成元、子生成元的顺序讲解的，我感觉不太好理解。按”子生成元$\to$生成元$\to$子生成矩阵$\to$生成矩阵”的顺序介绍，似乎更容易理解矩阵中的0和1所代表的的物理意义。

子生成元和生成元

  子生成元$g^{(i,j)}$：$(n,k,N)$卷积码有$kn$个子生成元$g^{(i,j)}$，其中$i=1,2,3,\cdots ,k$，$j=1,2,3,\cdots ,n$。每个子生成元是一个$N$维行向量，$g^{(i,j)}$的第$m$位写成$g_m^{(i,j)}$，$m=0,1,2,\cdots ,N-1$，$g^{(i,j)}$可以表示为：$$g^{(i,j)}=g_0^{(i,j)}{g}_1^{(i,j)}\cdots g_{N-1}^{(i,j)}$$ $g_m^{(i,j)}$表示第$m$组输入寄存器比特的第$i$位与第$j$个模2和加法器的连接关系，其中1表示相连，0表示不相连。
  生成元$g^{(i)}$：$(n,k,N)$卷积码有$k$个生成元$g^{(i)}$，其中$i=1,2,3,\cdots ,k$。每个子生成元是一个$Nn$维行向量，$g^{(i)}$可以表示为：$$g^{(i)}=g_0^{(i,1)}{g}_0^{(i,2)}\cdots g_0^{(i,n)}\cdots g_{N-1}^{(i,1)}{g}_{N-1}^{(i,2)}\cdots g_{N-1}^{(i,n)}$$

子生成矩阵和生成矩阵

  子生成矩阵$g_m$：$(n,k,N)$卷积码有$N$个子生成矩阵$g_m$，其中$m=0,1,2,\cdots ,N-1$。每个子生成矩阵由$kn$个$g_m^{(i,j)}$组成的$k\times n$矩阵，$g_m$可以表示为：$$g_m=\left[\begin{array}{cccc}{g}_m^{(1,1)}& g_m^{(1,2)}& \cdots & g_m^{(1,n)}\\ g_m^{(2,1)}& g_m^{(2,2)}& \cdots & g_m^{(2,n)}\\ ⋮& ⋮& \ddots & ⋮\\ g_m^{(k,1)}& g_m^{(k,2)}& \cdots & g_m^{(k,n)}\end{array}\right]$$
  基本生成矩阵$G_B$：$(n,k,N)$卷积码的基本生成矩阵$G_B$由$N$个子生成矩阵$g_m$组成，是一个$k\times Nn$矩阵。$$G_B=\left[\begin{array}{cccc}{g}_0& g_1& \cdots & g_{N-1}\end{array}\right]$$
  生成矩阵$G_{\infty }$：$(n,k,N)$卷积码的生成矩阵$G_{\infty }$是一个半无穷矩阵，$G_{\infty }$可以表示为：$$G_{\infty }=\left[\begin{array}{ccccccccc}{g}_0& g_1& \cdots & g_{N-2}& g_{N-1}& 0& 0& 0& \cdots \\ 0& g_0& g_1& \cdots & g_{N-2}& g_{N-1}& 0& 0& \cdots \\ 0& 0& g_0& g_1& \cdots & g_{N-2}& g_{N-1}& 0& \cdots \\ \cdots & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \end{array}\right]$$ $G_{\infty }$的每$k$行（$g_m$有$k$行）是前一$k$行向右移位$n$列（$g_m$有$n$列）的结果。

生成矩阵的作用

  假设移位寄存器的初态都是0，编码器对每组$k$个信息比特的输入产生一组$n$个编码比特输出。当第一组$k$个信息比特（用$M(0)$表示）输入时，输出为$Y(0)=M(0)g_0$（对比$G_{\infty }$的第一列，观察规律），相当于$M(0)$中的$k$个比特输入到与其相连的模2和加法器后运算的结果。当第二组$k$个信息比特（用$M(1)$表示）输入时，前一组$k$个信息比特向后移位，输出为$Y(1)=M(0)g_1+M(1)g_0$（对比$G_{\infty }$的第二列，观察规律），相当于$M(0)$和$M(1)$中的$2k$个比特输入到与其相连的模2和加法器后运算的结果。以此类推，可得$$Y(N)=M(0)g_{N-1}+M(1)g_{N-2}+\cdots +M(N-2)g_1+M(N-1)g_0（对比G_{\infty }的第N列，观察规律)$$此时，再有一组信息比特（用$M(N)$表示）输入时，$M(0)$被移除移位寄存器而消失。
（我有点口拙，这块可能描述的不是很清楚，主要靠意会 😄，后面举例子）

举例

$(n,1,N)$卷积码

  给定子生成元：$g^{(1,1)}=10011$，$g^{(1,2)}=11101$
  由子生成元可得：$n=2$，$N=5$
  生成元为：$g^{(1)}=1101011011$
  子生成矩阵为：$g_0=\left[\begin{array}{c}11\end{array}\right]$，$g_1=\left[\begin{array}{c}01\end{array}\right]$，$g_2=\left[\begin{array}{c}01\end{array}\right]$，$g_3=\left[\begin{array}{c}10\end{array}\right]$，$g_4=\left[\begin{array}{c}11\end{array}\right]$
  生成矩阵为：$$G_{\infty }=\left[\begin{array}{ccccccccc}11& 01& 01& 10& 11& 00& 00& 00& \cdots \\ 0& 11& 01& 01& 10& 11& 00& 00& \cdots \\ 0& 0& 11& 01& 01& 10& 11& 00& \cdots \\ \cdots & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \end{array}\right]$$
  编码器原理图为：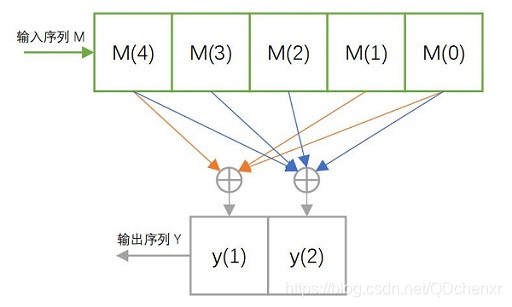
  当输入序列为$m=110110000\cdots$时，输出序列为$y=11100000111111011100\cdots$

$(n,k,N)$卷积码

  给定子生成元：$$g^{(1,1)}=100，g^{(1,2)}=000，g^{(1,3)}=101$$$$g^{(2,1)}=000，g^{(2,2)}=100，g^{(2,3)}=110$$
  由子生成元可得：$n=3$，$k=2$，$N=3$
  生成元为：$$g^{(1)}=101000001$$$$g^{(2)}=011001000$$
  子生成矩阵为：$$g_0=\left[\begin{array}{ccc}1& 0& 1\\ 0& 1& 1\end{array}\right]，g_1=\left[\begin{array}{ccc}0& 0& 0\\ 0& 0& 1\end{array}\right]，g_2=\left[\begin{array}{ccc}0& 0& 1\\ 0& 0& 0\end{array}\right]$$
  生成矩阵为：$$G_{\infty }=\left[\begin{array}{ccccccc}101& 000& 001& 000& 000& 000& \cdots \\ 011& 001& 000& 000& 000& 000& \cdots \\ 000& 101& 000& 001& 000& 000& \cdots \\ 000& 011& 001& 000& 000& 000& \cdots \\ 000& 000& 101& 000& 001& 000& \cdots \\ 000& 000& 011& 001& 000& 000& \cdots \\ \cdots & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \end{array}\right]$$
  编码器原理图为：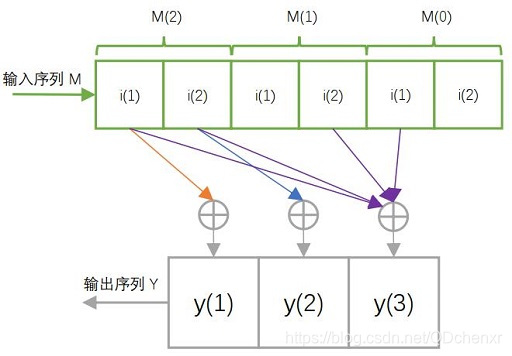
  当输入序列为$m=10110000\cdots$时，输出序列为$y=101110000001000\cdots$

参考：卷积码
   通信原理（第二版）张会生 著