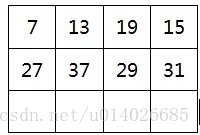
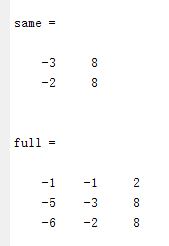一、卷积定义
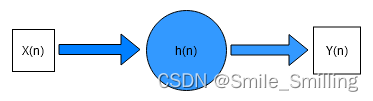
卷积是两个变量在某范围内相乘后求和的结果。如果卷积的变量是g(n)序列和h(n),则卷积的结果
y ( n ) = g ( n ) ∗ h ( n ) = ∑ i = − ∞ ∞ g ( i ) h ( n − i ) y(n) = g(n) * h(n) = \sum_{i = -\infty}^{\infty}g(i)h(n-i) y(n)=g(n)∗h(n)=i=−∞∑∞g(i)h(n−i)
其中星号*表示卷积。当时序n=0时,序列h(-i)是h(i)的时序i取反的结果;时序取反使得h(i)以纵轴为中心翻转180度,所以这种相乘后求和的计算法称为卷积和,简称卷积。另外,n是使h(-i)位移的量,不同的n对应不同的卷积结果。
二、计算
假设有两个序列 g ( n ) = 2 x 2 + x + 1 g(n) = 2x^2 + x + 1 g(n)=2x2+x+1
h ( n ) = 3 x 3 + 0.5 x 2 + 2 x + 1 h(n) =3x^3+ 0.5x^2 + 2x+1 h(n)=3x3+0.5x2+2x+1
2.1直接相乘
y = gh
则 y ( n ) = 6 x 5 + 4 x 4 + 7.5 x 3 + 4.5 x 2 + 3 x + 1 y(n) =6x^5+4x^4+7.5x^3+4.5x^2+3x+1 y(n)=6x5+4x4+7.5x3+4.5x2+3x+1
最后y(n)的项数等于g(n)和h(n)项数之和-1
2.2 一维阵列相乘
g ( n ) = [ 1 , 1 , 2 ] g(n) = [1, 1, 2] g(n)=[1,1,2]
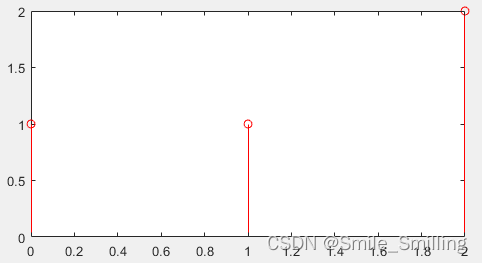
h ( n ) = [ 1 , 2 , 0.5 , 3 ] h(n) = [1,2,0.5,3] h(n)=[1,2,0.5,3]
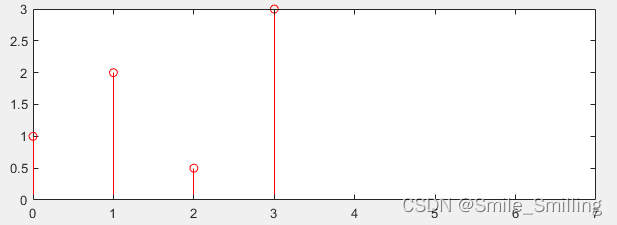 (1)取g(0)乘以h(n)右移0位;
(1)取g(0)乘以h(n)右移0位;
得到 y ( 0 ) = [ 1 , 2 , 0.5 , 3 ] y(0) =[1,2,0.5,3] y(0)=[1,2,0.5,3]

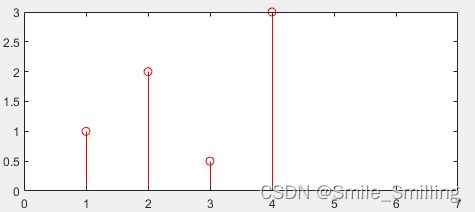
(2)取g(1)乘以h(n)右移1位;
得到 y ( 1 ) = [ 0 , 1 , 2 , 0.5 , 3 ] y(1) =[0,1,2,0.5,3] y(1)=[0,1,2,0.5,3]
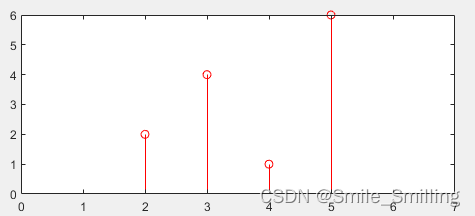
(3)取g(2)乘以h(n)右移2位;
得到 y ( 2 ) = [ 0 , 0 , 2 , 4 , 1 , 6 ] y(2) =[0,0,2,4,1,6] y(2)=[0,0,2,4,1,6]
(4)将所有数值叠加,得到
y ( n ) = y ( 0 ) + y ( 1 ) + y ( 2 ) = [ 1 , 3 , 4.5 , 7.5 , 4 , 6 ] y(n)=y(0)+y(1)+y(2) = [1,3,4.5,7.5,4,6] y(n)=y(0)+y(1)+y(2)=[1,3,4.5,7.5,4,6]
2.3 翻褶、移位、相乘、相加
(1)翻褶
由卷积公式,可以看出
y ( n ) = g ( n ) ∗ h ( n ) = ∑ i = − ∞ ∞ g ( i ) h ( n − i ) y(n) = g(n) * h(n) = \sum_{i = -\infty}^{\infty}g(i)h(n-i) y(n)=g(n)∗h(n)=i=−∞∑∞g(i)h(n−i)
h(n-i)取n为0,得到h(-i),h(-i)可由h(i)对Y轴做翻转得到,所以需要经过翻褶这个步骤,翻褶之后H(n)如下图所示(这里将翻转之后的定义为H(n))
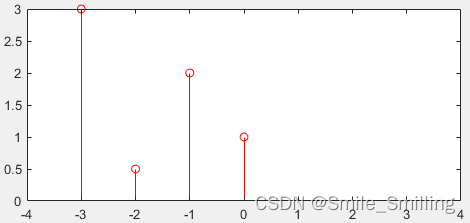
(2)移位
求取y(0)时,将H(n)右移0位;y(1)时,将H(n)右移1位;以此类推
(3)相乘
以y(0)为例,g(n)和H(n)如下
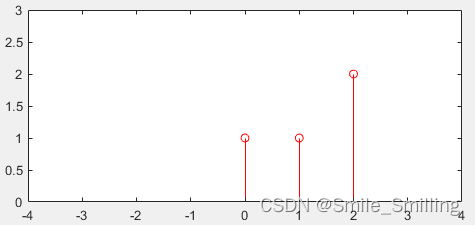

将g(n)和H(n)每一项对应相乘,得到[1,0,0]
(4)相加
y ( 0 ) = ∑ i = 0 2 g ( i ) h ( − i ) = ∑ i = 0 2 g ( i ) H ( i ) = 1 + 0 + 0 = 1 y(0) =\sum_{i = 0}^{2}g(i)h(-i)= \sum_{i = 0}^{2}g(i)H(i) =1+0+0=1 y(0)=i=0∑2g(i)h(−i)=i=0∑2g(i)H(i)=1+0+0=1
按照以上步骤2~4,分别求出y(n)其余数值,这里n的取值为g(n)和h(n)阵列长度之和减1