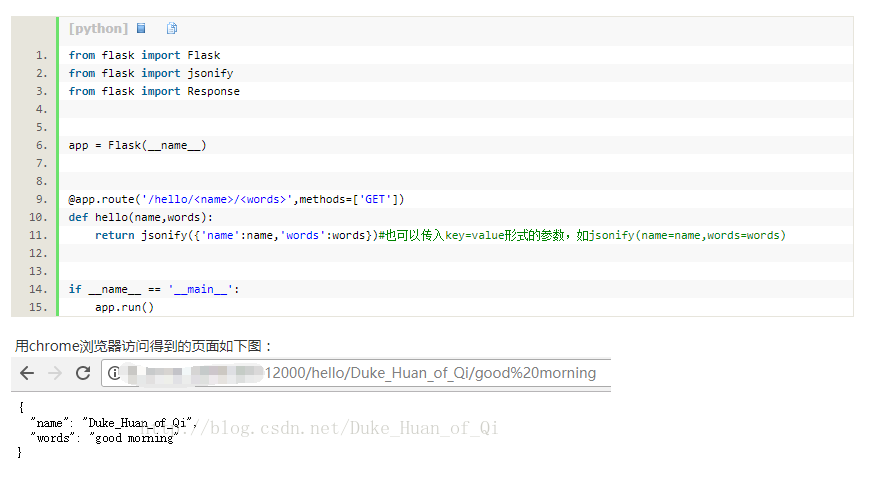
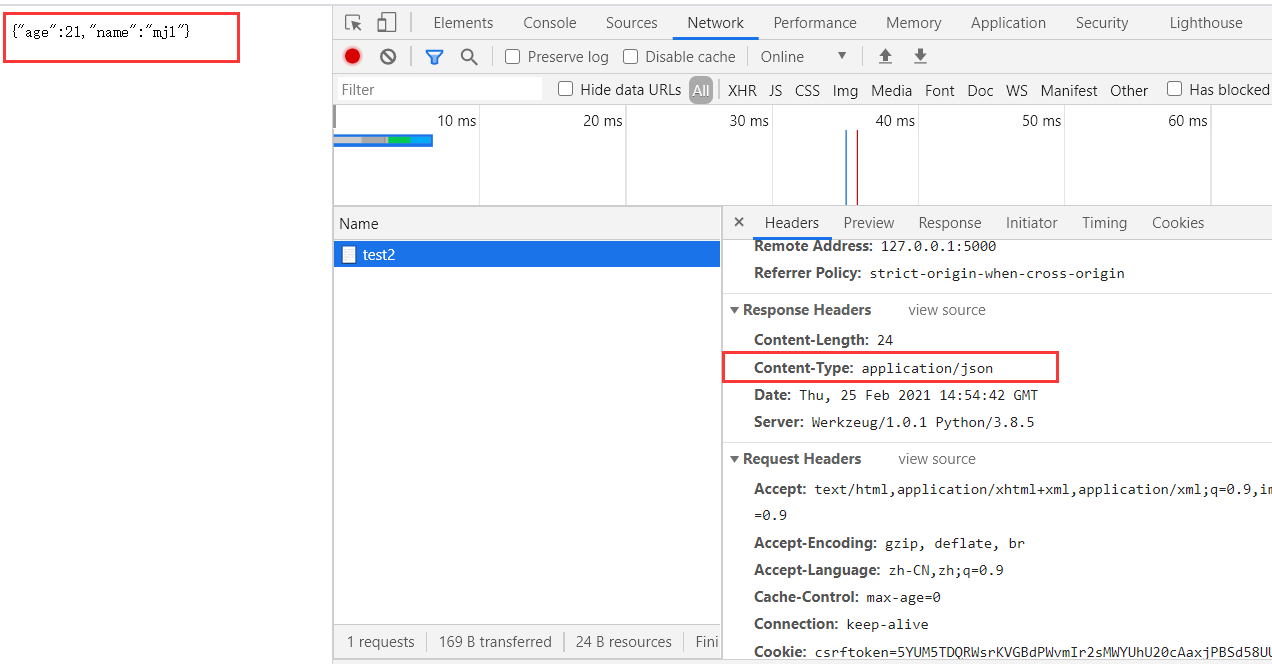
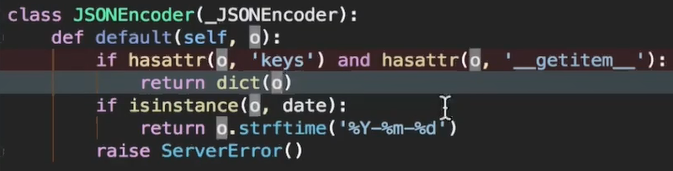
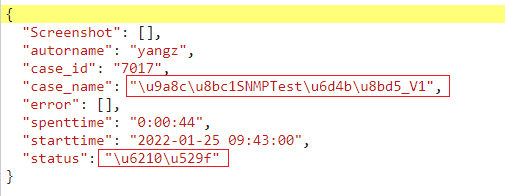
1、离散⼆维卷积公式
 

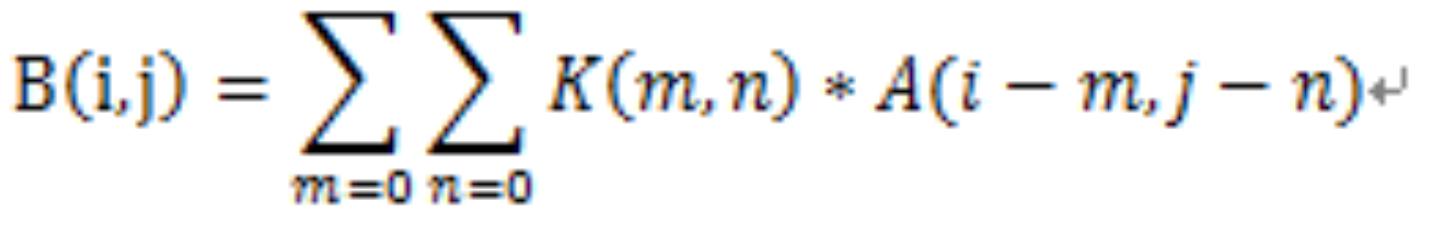
其中A为被卷积矩阵，K为卷积核，B为卷积结果，该公式中，三个矩阵的排序均从0开始。

卷积核、滤波器通常为较小尺寸的矩阵，比如3×33×3、5×55×5等，数字图像是相对较大尺寸的2维（多维）矩阵（张量），图像卷积运算与相关运算的关系如下图所示，其中FF为滤波器，XX为图像，OO为结果

二、计算

现在对于上面卷积过程进行分析：我们用来做例子的 M1矩阵为 m×m(3×3)二维矩阵（被卷积矩阵），M2 为 n×n(2×2)的二维矩阵（卷积核）。

矩阵M1

1          2         3

4          5         6

7          8        9

矩阵M2

1        2

3        4

翻转

4        3 

2        1

被卷积矩阵扩展到(m+n)×(m+n)大小，将扩展部分用 0 代替，将卷积核 K 从左上角顺序地行移动，再换行，继续，直到抵达右下角。将对应元素相乘后相加。

0        0        0        0        0

0        1        2        3        0

0        4        5        6        0

0        7        8        9        0

0        0        0        0        0

部分元素的计算

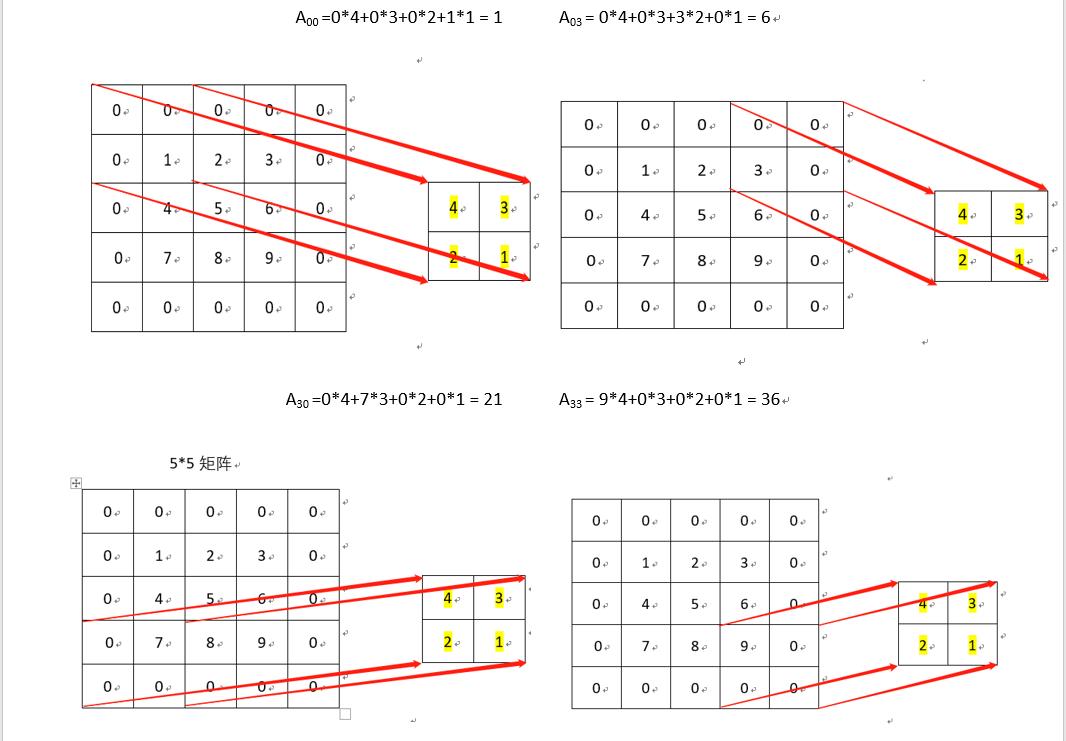
依次类推，剔除为 0 的元素，5×5 矩阵结果为 4×4 矩阵，卷积计算结束

1          4           7         6

7          23        33        24                 

19        53        63        42

21        52        59        36

3、使用python计算

from sympy import *
import numpy as np
from scipy import signalM3 = np.array([[1,2,3],[4,5,6],[7,8,9]])
M4 = np.array([[1,2],[3,4]])print("full卷积：",signal.convolve2d(M3, M4,'full'))
print("same卷积：",signal.convolve2d(M3, M4,'same'))
print("valid卷积：",signal.convolve2d(M3, M4,'valid'))