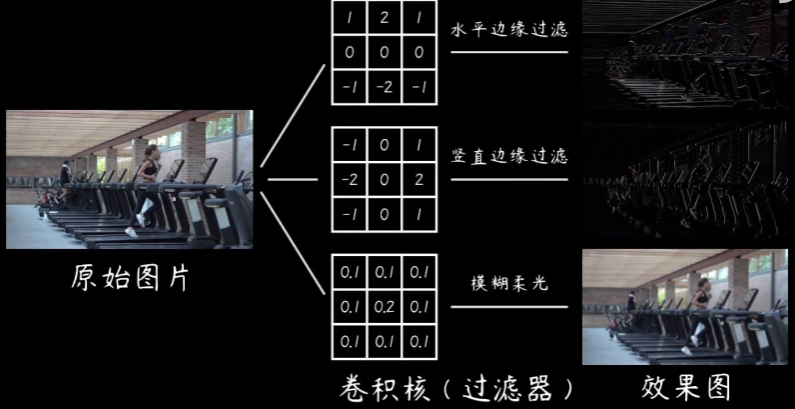
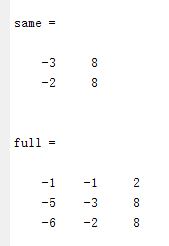矩阵卷积、矩阵相乘的转化

article/2025/9/12 7:53:52

两个矩阵卷积转化为矩阵相乘形式——Matlab应用(这里考虑二维矩阵，在图像中对应)两个图像模糊（边缘）操作，假设矩阵A、B，A代表源图像，B代表卷积模板，那么B的取值决定最后运算的结果。

Matlab中的应用函数——conv2（二维卷积，一维对应conv）

函数给出的公式定义为：

同一维数据卷积一样，它的实质在于将卷积模板图像翻转（旋转180），这里等同于一维信号的翻转，然后将卷积模板依次从上到下、从左到右滑动，计算在模板与原始图像交集元素的乘积和，该和就作为卷积以后的数值。

为了验证后续矩阵卷积转化为矩阵相乘，这里给出的conv2的实例描述：

假设矩阵A（4*3）、B（2*3）如下：

首先，B需要旋转180，

命令旋转2次90即可：

B = rot90(rot90(B));或者B = rot90(h,2); 结果为：

其次：命令conv2函数：

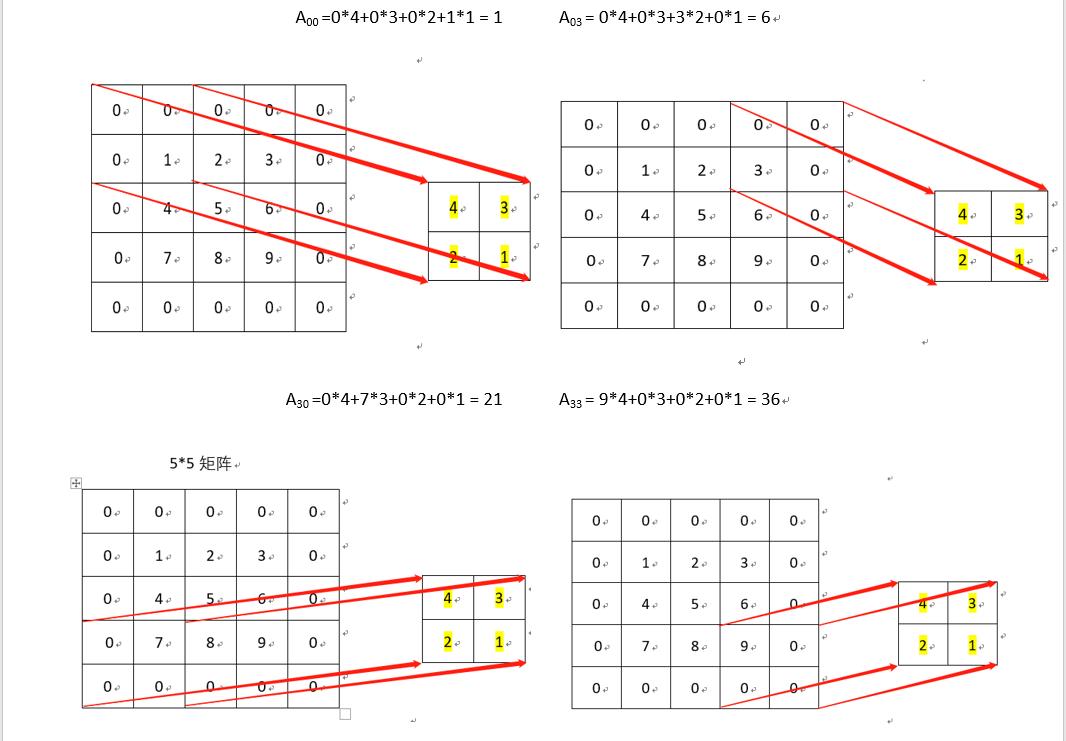
C = conv2(A,B，‘shape’),该函数的具体操作图示：

依次计算直至结束，结果数据为：

shape的取值有三种，full代表返回卷积以后的全部数据，size为(mA+mB-1,nA+nB-1)的数据；same代表返回卷积以后的原图size (mA,nA)的部分数据；valid返回size为(mA-mB+1,nA-nB+1)的数据，指的是模板元素全部参加运算的结果数据，即源图像和模板的交集为模板。

矩阵卷积转化为矩阵相乘，网上也有很多方法，通俗化表示为：

A×B = B1*A1;

需要针对原始数据与模板数据做变换，变换过程如下：

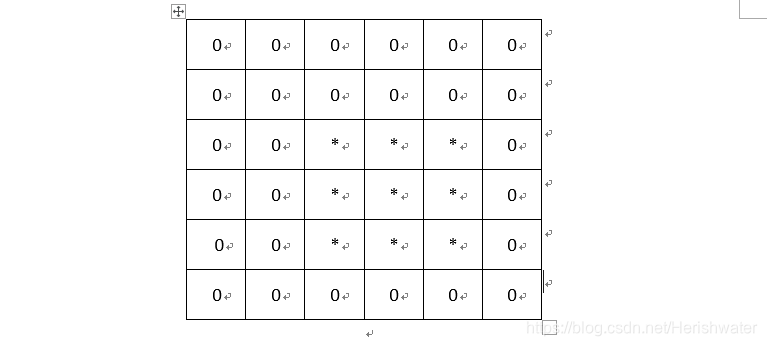
首先进行周期延拓，补零：

M = mA+mB-1 = 5; N = nA+nB-1 = 5，对应卷积以后full数据大小。

那么初次换换的A和B为：

其次对A1和B1分别进行变换

转化B1——针对B1以及转换矩阵方法为：

将B1中的每一行向量依次按照B转化为一个方形矩阵Ba~Be，然后针对于每一个方形矩阵按照B矩阵组合成一个新的矩阵B1。B1矩阵的大小为（（mA+mB-1）*（nA+nB-1），（mA+mB-1）*（nA+nB-1））。

转化A1——堆叠向量式

将上个步骤转换的A1按照行向量顺寻依次转化为一个列向量，那么列向量的大小为（（mA+mB-1）*（nA+nB-1），1）大小。

针对实例：具体代码为：

周期延拓：

转化A——>A1

   [m1,n1] = size(A);  [m2,n2] = size(B);m=m1+m2-1;n=n1+n2-1;AA = padarray(A,[m2-1,n2-1],'post');%%%补零BB = padarray(B,[m1-1,n1-1],'post');%%%补零AA =AA';A1 = AA(:);%%%%

转化B——>B1

   B2(1,:) = BB(1,:);for i =2:mB2(i,:) = BB(m-i+2,:);end %%%矩阵a ~ e的重新赋值B4 = zeros(n,n);%%%%%%%每一行转化的方阵B1 = zeros(m*n,m*n);%%%%%最后的矩阵for i =1:m%%%%%%%%几维向量B = B2(i,:);if sum(sum(abs(B))==0)B4 = zeros(n,n);elsefor j = 1:n%%%%%%%元素for k =0:n-1%%%%%%%%位置(搞定一行向量转化为方阵的形式)t = mod(j+k,n);if t==0t = n;end  %%%end ifB4(t,k+1) = B(j);end %%%end forend  %%%end forfor  k =0:m-1%%%%%%%%每一个转换矩阵在大矩阵中的位置编号（搞定小方阵在大阵中的位置转化为大方阵的形式）t = mod(i+k,m);if t==0t = m;end  %%%end ifB1(k*n+1:(k+1)*n,(t-1)*n+1:t*n) = B4;end  %%%end forend %%%end if else end  %%%end for

结果数据转化：

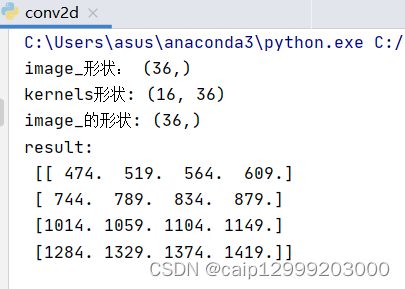
   Result = B1*A1;Result = reshape(Result,n,m);Result = Result';

得到的结果等同于conv2的数据结果：

利用matlab接口更快的实现方法：

还是以5 * 5的原始数据与3*3的卷积核为例子：

代码如下：

dd_data = [1,2,4,5,6;6,8,9,1,3;6,8,9,2,4;7,3,5,7,5;1,5,8,9,3]; % 5 *  5
f_k = [3,4,5;6,7,8;3,2,1]; % 3 * 3
dd_data_f_k = conv2(dd_data,f_k,'full'); % matlab 函数接口
dd_data1 = padarray(dd_data,[2 2],'both'); % 扩充原始数据
v_dd_data = im2col(dd_data1,[3 3]);% 块数据向量化
f_k1 = f_k(:);
f_k1 = f_k1(end : -1 :1);
f_k1 = f_k1'; % 卷积核的表示
dd_data_f_k1 = f_k1 * v_dd_data; % 卷积转化为相乘
dd_data_f_k1 = reshape(dd_data_f_k1,[7 7]); % 转化为结果数据