二维卷积/矩阵卷积的计算方程

设有矩阵A和矩阵B，它们的卷积结果矩阵的元素可由下列公式计算得来：

$$C(j,k)=\sum_p \sum_q A(p,q) B(j-p+1,k-q+1)$$
其中的index只要在A，B中valid都要参与运算。
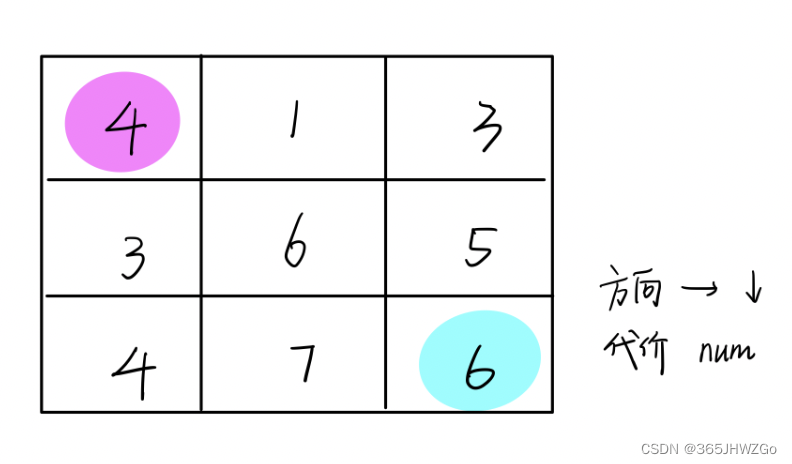
举例来说，令矩阵M为卷积核矩阵，矩阵I为图像矩阵，其元素如下：
$$M=\begin{bmatrix}1 & 2 \\3 & 4 \\\end{bmatrix},I=\begin{bmatrix}1 & 2 & 3 \\2 & 3 & 4 \\3 & 4 & 5 \\\end{bmatrix}$$
要计算二者的卷积，首先令卷积核旋转 $180^\circ$，那么M的变态过程如下
首先行翻转：
$$M_1=\begin{bmatrix}3 & 4 \\2 & 1 \\\end{bmatrix}$$
然后列翻转：
$$M_2=\begin{bmatrix}4 & 3 \\1 & 2 \\\end{bmatrix}$$
（为什么称为180°翻转呢，这可以看作是原来的矩阵一行一行写成一个行向量，1 2 3 4，然后倒着写回去(180°翻转)，变成 4 3 2 1，再写成矩阵的形式，跟上面的变化结果是一样的。）为了便于书写，将反转后的矩阵记为 K。
如果将矩阵的重叠看作是二维平面上两个矩形的相交，那么相交有无重叠的情况也分为几种：
1. 不相交，没有重叠的部分

2. 上边相交，重叠区域在大矩形的上边。

1. 左边相交，重叠区域在大矩形的左边
   
   上两种情况的一个交集就是在大矩形的左上角有相交：
   
2. 完全重叠的相交，小矩形套在大矩形里面。
   
3. 右边的相交，重叠区域在大矩形的右边。
   

4. 下边缘的相交，重叠区域在大矩形的下边。
   
   右下的相交，重叠区域在大矩形的右下角。
   
   类比卷积中，两个矩阵的元素的重叠也有这么几种。那么最终我们要使用这个相交产生的并集或者交集，或者是并集的一部分作为最后卷积结果的尺寸。
   在matlab的conv2函数里有个’shape’参数，是这样解释的：

   Subsection of the convolution, specified as one of these values:

   1. ’full’ — Return the full 2-D convolution.
   2. ‘same’ — Return the central part of the convolution, which is the same size as A.
   3. ‘valid’ — Return only parts of the convolution that are computed without zero-padded edges.

   现在我们默认conv2（I,M）,即第一个array的size比第二个array的size要大一些。（如果相反，那么这三种情况又不太一样，此处不涉及）。分别来看一下

Valid 型卷积

这种类型只取用M(自己计算时是K，即180°反转后的矩阵)完全与I重叠的情况，就像是矩阵相交的第4种情况。完全不给任何矩阵补0，最终的卷积结果矩阵与M的尺寸一样(小矩阵的尺寸)。
就我们的M和I的例子，设结果矩阵为V，一个个元素计算的话，其过程如下：
$V_{11}= 4*1+3*2+2*2+1*3=17$
如下图，

$V_{12}= 4*2+3*3+2*3+1*4=27$

$V_{21}= 4*2+3*3+2*3+1*4=27$

$V_{22}= 4*3+3*4+2*4+1*5=37$

最终Valid型结果为：

$$V=\begin{bmatrix}17 & 27 \\27 & 37 \\\end{bmatrix}$$

Same型卷积

这种类型除了包含valid型的所有结果之外，还要包含小矩阵与大矩阵的右边缘、以及下边缘有重叠的情况。就像是矩阵相交的第4、第5和第6种情况。给矩阵I补0，已完成右边缘重叠和下方时的计算。最终的卷积结果矩阵与I的尺寸一样(大矩阵的尺寸)。
就我们的M和I的例子，设结果矩阵为S。I矩阵补零后为

$$I=\begin{bmatrix}1 & 2 & 3 &0 \\2 & 3 & 4 &0\\3 & 4 & 5 &0 \\0 & 0 & 0& 0\\\end{bmatrix}$$
(说明：其实给矩阵补零后相交情况就只有4那种了)
一个个元素计算的话，其过程如下： $S_{11}, S_{12}, S_{21}, S_{22}$与前面计算的V一样。
$S_{13}= 4*3+3*0+2*4+1*0=20$
$S_{23}= 4*4+3*0+2*5+1*0=26$
$S_{31}= 4*3+3*4+2*0+1*0=24$
$S_{32}= 4*4+3*5+2*0+1*0=31$
$S_{33}= 4*5+3*0+2*0+1*0=20$

最终Same型结果为：
$$S=\begin{bmatrix}17 & 27 & 20\\27 & 37 & 26 \\24& 31&20\\\end{bmatrix}$$
结合卷积的物理意义，就是加权叠加，再回头看一下计算.
$S_{11}$是矩阵K和 $I_{11}$周围的像素加权求和，这里的周围指的是右，右下，下还有其本身。
卷积结果矩阵中的其他元也是这样解释。

full 型卷积

包含所有重叠的情况，在Same型基础上添加了小矩阵与大矩阵左边重叠的情况。即矩形相交的2，3，4，5种情况。这也是最复杂的一类。
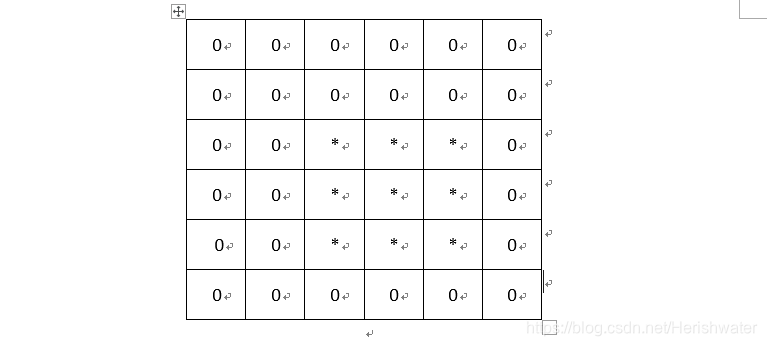
如果从valid转换为same还比较好理解的话，再转换为full原理也是一样的，不过这次I矩阵是在左边，上边，右边，下边都要补零，为什么要这么做呢？请看下图（博主为了偷懒，就把好几种情况放一起了）：

是不是必须要前后左右全方位补零才可以呢？而且如果M的size更大一些的话，补的就不止是一行一列的0了。（补就是pad，pad就是补）
最终补零后的I矩阵变成：

$$I=\begin{bmatrix}0&0 & 0 & 0 &0 \\0&1 & 2 & 3 &0 \\0&2 & 3 & 4 &0\\0&3 & 4 & 5 &0 \\0&0 & 0 & 0 &0 \\\end{bmatrix}$$
(再次强调：其实给矩阵补零后相交情况就只有4那种了)
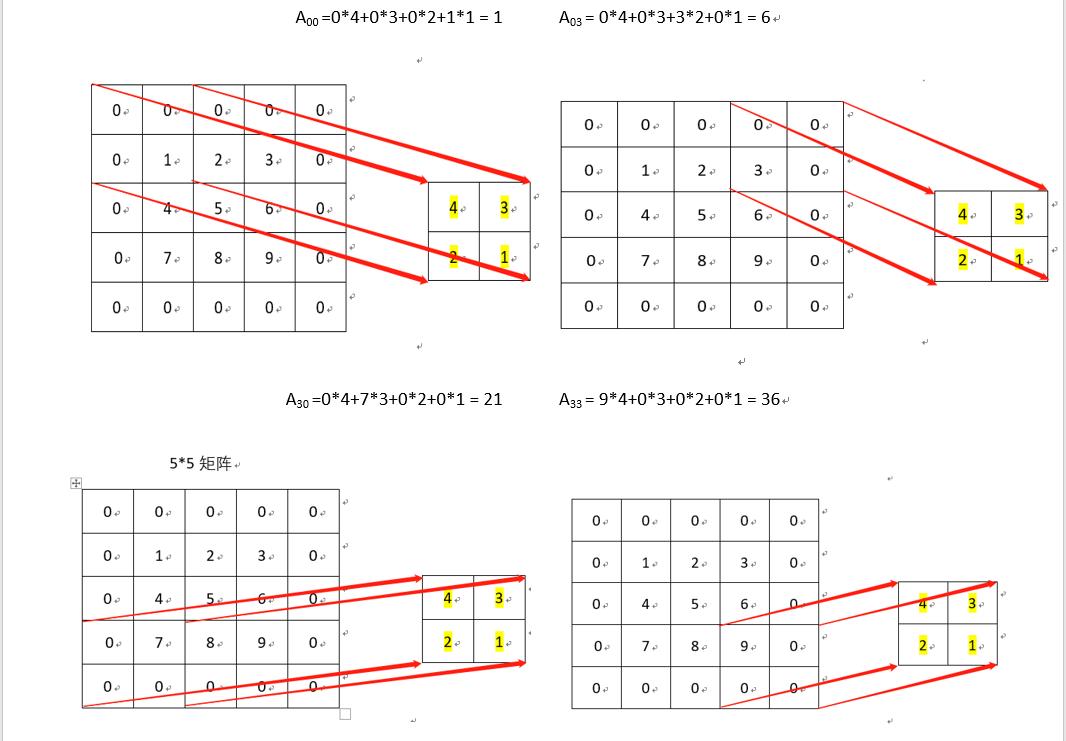
就我们的M和I的例子，设结果矩阵为F。
$F_{11}= 4*0+3*0+2*0+1*1=1$
$F_{12}= 4*0+3*0+2*1+1*2=4$
$......$
依次类推

最终，Full型的卷积结果为：

$$F=\begin{bmatrix}1 & 4&7&6\\5&17 & 27 & 20\\9&27 & 37 & 26 \\9&24 & 31 & 20 \\\end{bmatrix}$$
结合卷积的物理意义，就是加权叠加，再回头看一下计算.
$F$矩阵中的元素也是矩阵$K$和 I <script type="math/tex" id="MathJax-Element-919">I</script>周围的像素加权求和，这里的“周围”则比较广义了，既有右边和下边，也有左边和上边。