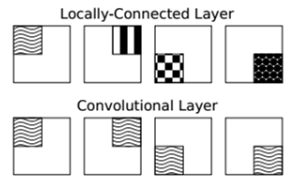
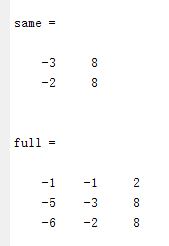【CV】卷积和逆卷积（转置卷积）详解

文章目录

【CV】卷积和逆卷积（转置卷积）详解
- 1. 卷积与转置卷积的关系
- 2. 普通卷积
- 3. 转置卷积
- - 3.1 形象化转置卷积过程
  - 3.2 转置卷积总结
- 4. 转置卷积函数
- - 4.1 转置卷积函数详解
  - 4.2 一般与特殊
  - - 4.2.1 一般反卷积的步骤
    - 4.2.2 卷积 (i+2p-k)/s 无法整除时
- 5. 参考

1. 卷积与转置卷积的关系

转置卷积又称反卷积，逆卷积。在主流的深度学习框架之中，如Tensorflow，Pytorch,Kreas中的函数名都是conv_transpose。
举个例子，将一个4X4的输入通过3X3的卷积核核进行普通卷积后（无padding,stride=1）,将得到2X2的输出。而转置卷积将一个2X2的输入通过同样的3X3的卷积核，将得到一个4X4的输出。
这看起来像是普通卷积的逆过程。事实上，这两者没有任何关系，操作过程也是不可逆的。

2. 普通卷积

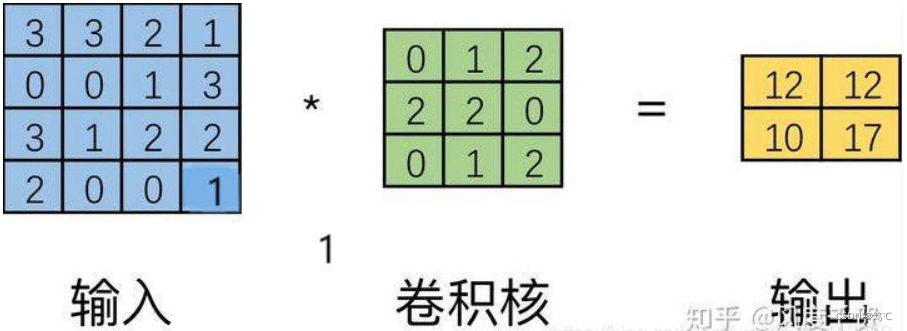
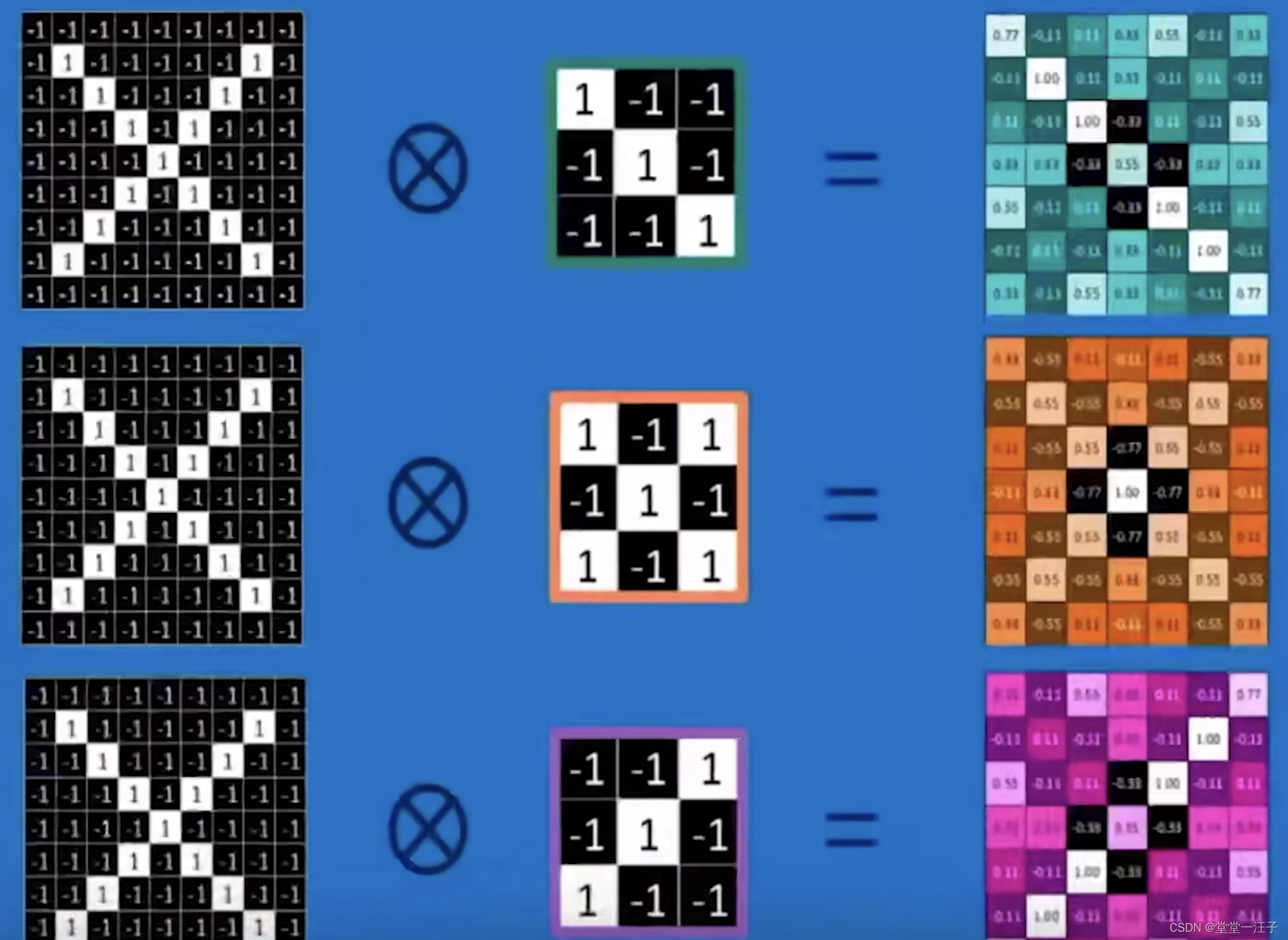
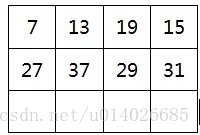
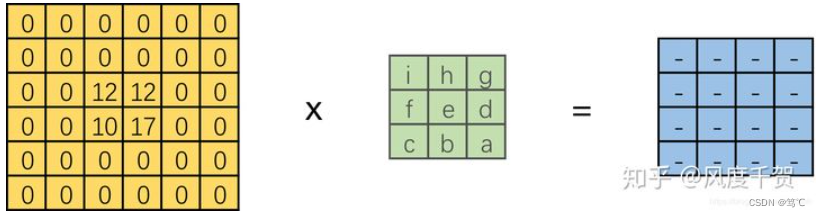
但在实际计算中，并不是通过卷积核在输入上进行滑动计算，效率太低，而是将卷积核转换为等效矩阵，将输入转化为向量，通过输入向量核卷积核矩阵的相乘获得输出向量。输出的向量经过整形便可得到我们的二维输出特征。
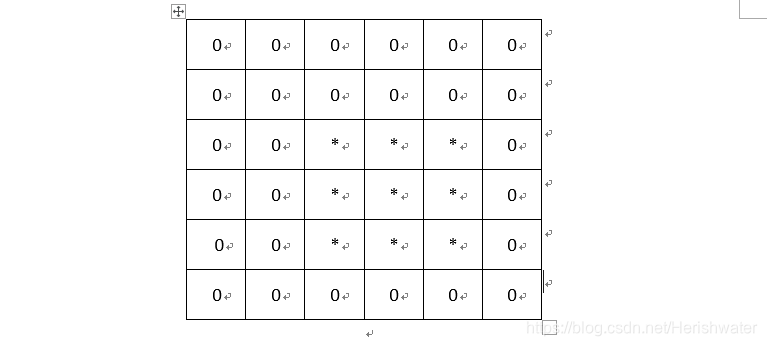
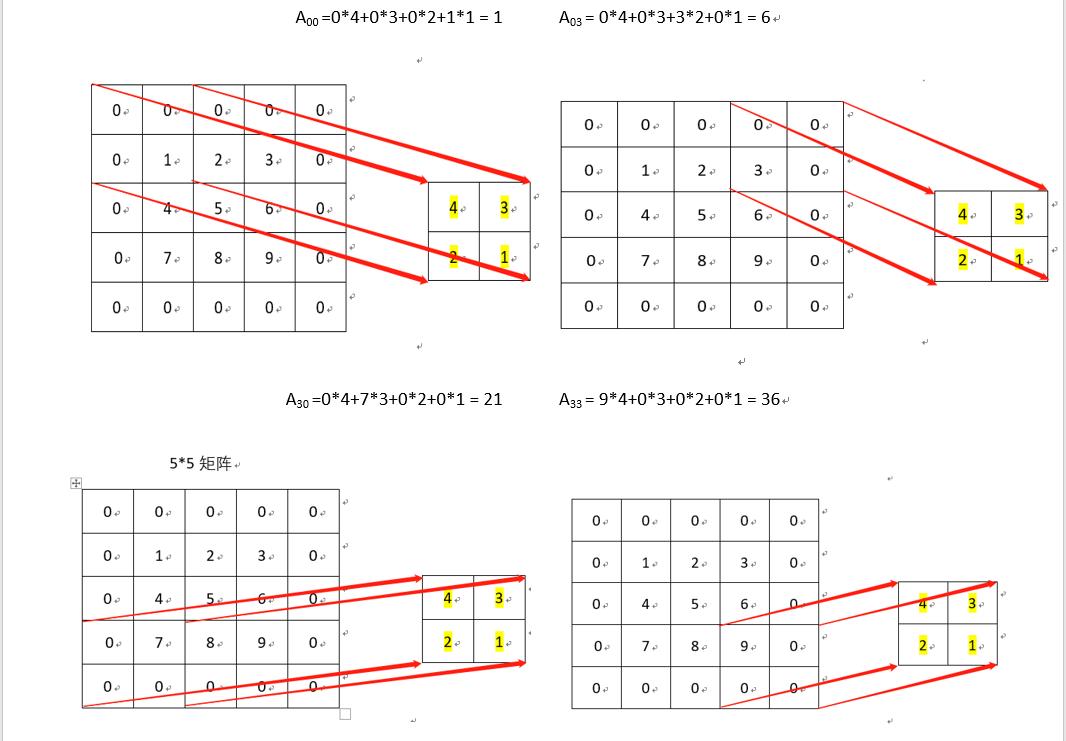
具体操作如下图所示，由于一个3X3的卷积核要在输入上不同位置卷积卷积4次，所以通过补0的方式，将卷积核分别置于一个4X4矩阵的四个角落，这样我们的输入可以直接和这四个4X4的矩阵进行卷积，而舍去了滑动操作。

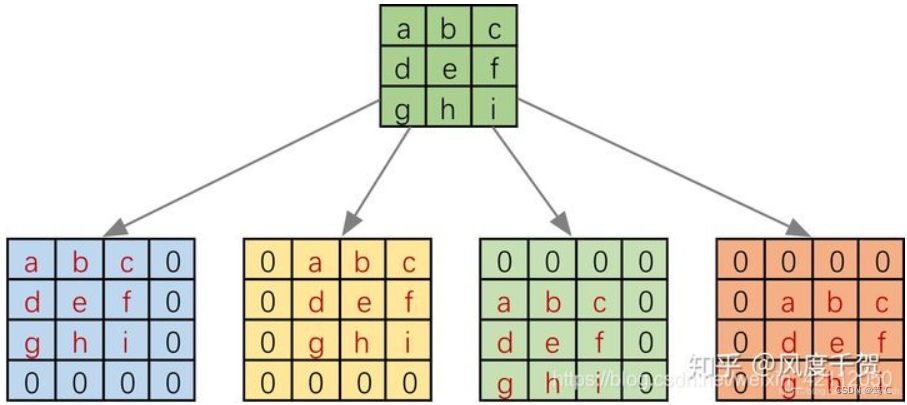
进一步我们将输入拉成长向量，四个4X4的卷积核也进行拼接，如下图：

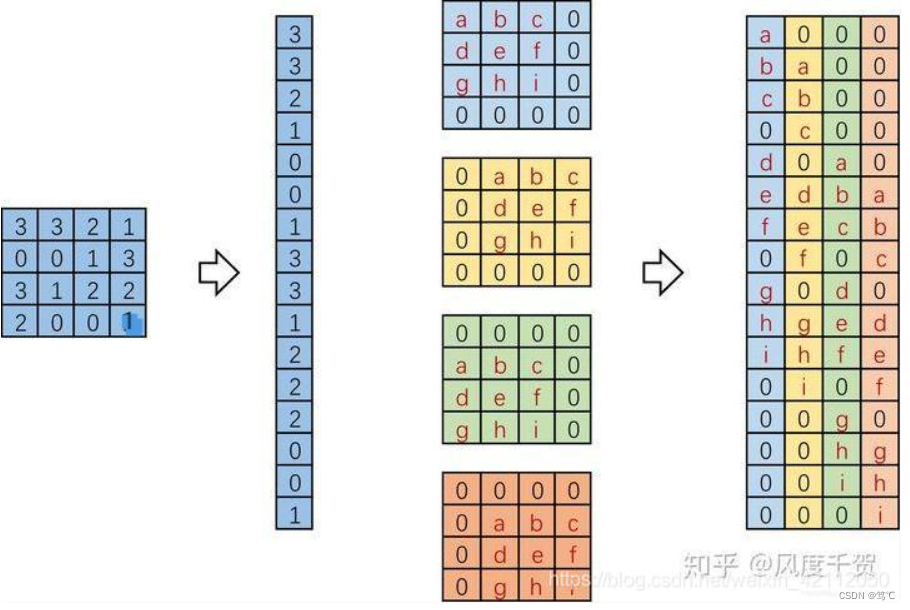
于是可以得到如下的结果，其实本身就是点积：

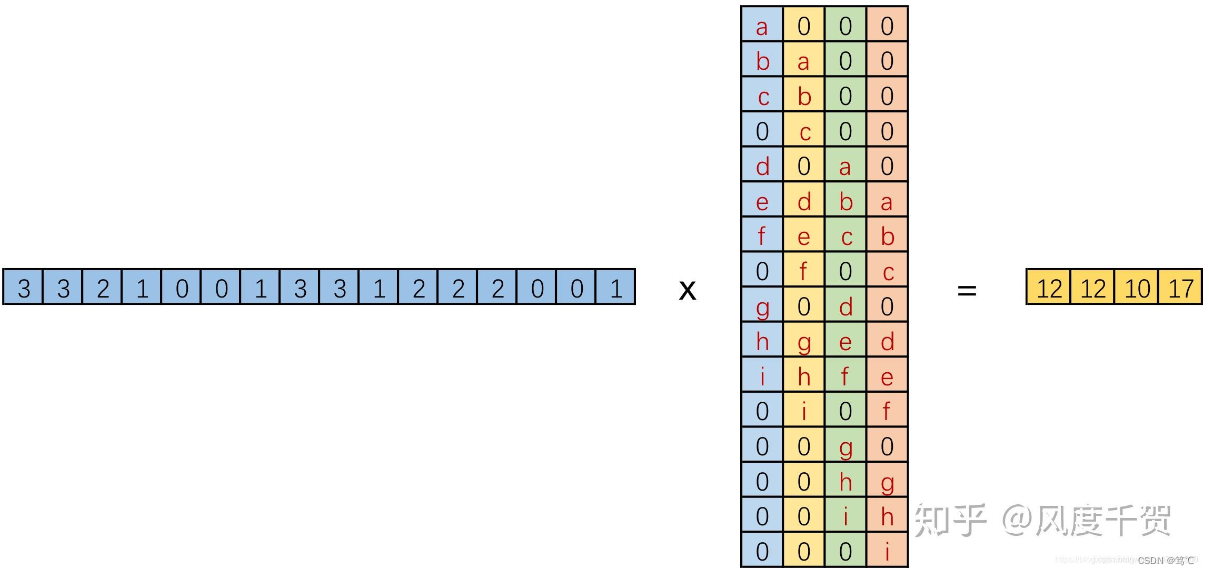
3. 转置卷积

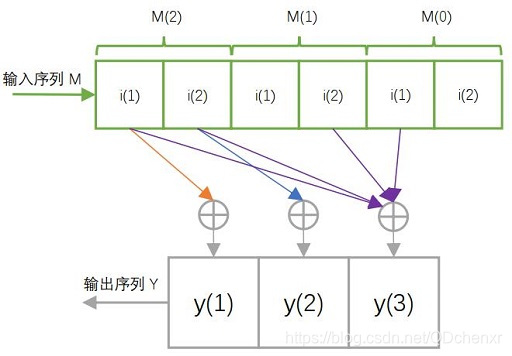
！！！重点思想！！！：我们将一个1X16的行向量乘以一个16X4的矩阵，得到一个1X4的行向量。那么反过来一个1X4的向量乘以一个4X16的矩阵不就是能得到一个1X16的行向量，这就是转置卷积的思想。

一般卷积操作（这里只考虑最简单的无padding，stride=1的情况），都将输入的数据越卷越小，根据卷积核大小的不同，和步长的不同，输出尺寸变化也很大。但是有时候，我们需要输入一个小的特征，输出更大的尺寸的特征。比如，图像语义分割中，往往要求最终的输出的特征尺寸和原始的输入尺寸相同，但是在网络卷积核池化的过程中特征图的尺寸逐渐变小，这里转置卷积便能派上用场。在数学上，转置卷积的操作非常简单，把正常的卷积操作反过来即可。

这里需要注意的是，这两个操作并不是可逆的，对于用一个卷积核，经过转置卷积操作后并不能恢复到原始的数值，只是保留了原始的形状。

3.1 形象化转置卷积过程

可视化转置卷积，以上式的第一列为例，

这里将输入还原为一个2X2的张量，新的卷积核由于左上角有非零值，可以计算得到右侧结果。进而对每一个列向量都可以做这样的变换，得到如下：

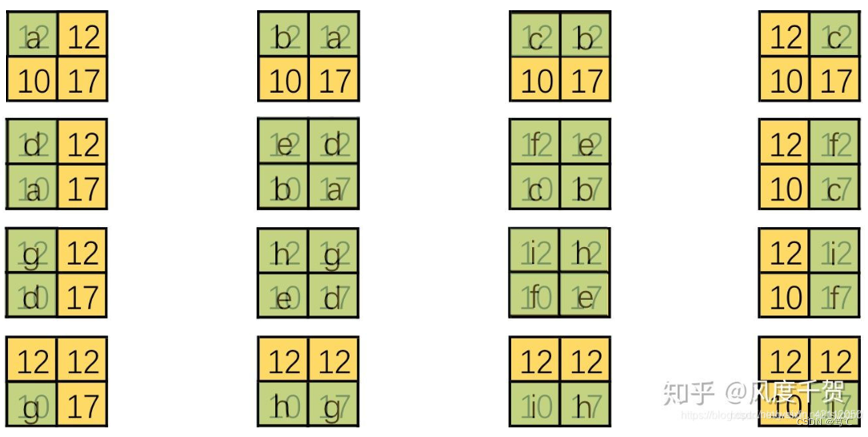
结合整体，仿佛是有一个更大的卷积核在2X2的大小的输入上滑动，但是输入太小，每一次卷积只能对应卷积核的一部分：

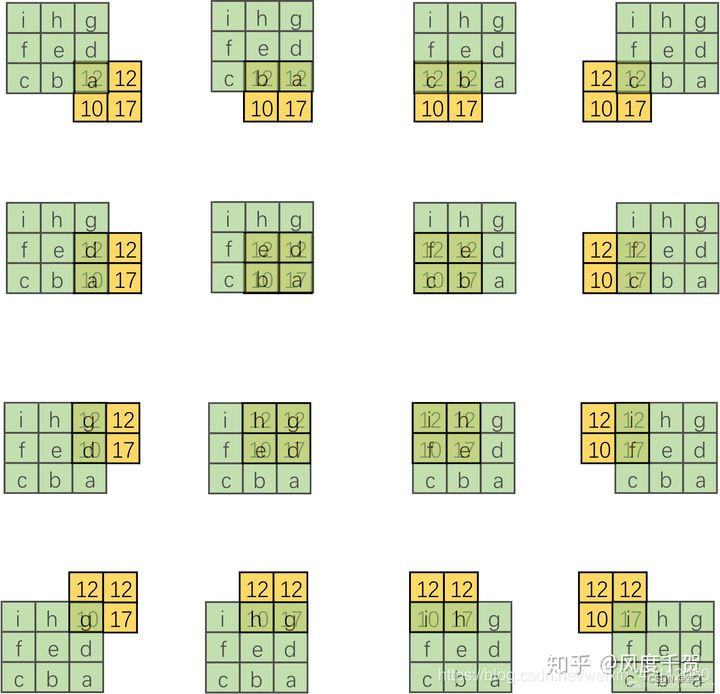
形象的描述：直接卷积是用一个小窗户看大世界，而转置卷积是用一个大窗户的一部分去看小世界。
这里需要注意。我们定义的卷积是左上角为a，右下角为i，但是在可视化卷积的过程中需要将卷积核旋转180度后再进行卷积。由于输入图像太小，我们按照卷积核的尺寸来进行补0操作，补0数量为2即3-1，这样就将一个转置卷积转换为对应的直接卷积。

3.2 转置卷积总结

转置卷积转换为直接卷积的步骤（这里只考虑stride=1 padding=0的情况）。

设卷积核大小为kXk，输入为方形图像。
（1）对输入进行四边补0，单边补0的数量为k-1
（2）将卷积核旋转180度，再新的输入上进行直接卷积

4. 转置卷积函数

nn.ConvTranspose2d(in_channels, out_channels, kernel_size, stride=1, padding=0, output_padding=0, bias=True)

in_channels (int) -输入信号的通道数
out_channels (int) - 卷积产生的通道数
kernel_size (int or tuple) - 卷积核的大小
stride (int or tuple, optional) - 卷积步长
padding (int or tuple, optional) - 输入的每条边补充0的层数
output_padding (int or tuple, optional) - 输出的每条边补充0的层数
dilation (int or tuple, optional) - 卷积核元素之间的间距
groups (int, optional) - 从输入通道到输出通道的阻塞连接数
bias (bool, optional) - 如果bias=True, 添加偏置

4.1 转置卷积函数详解

符号规定
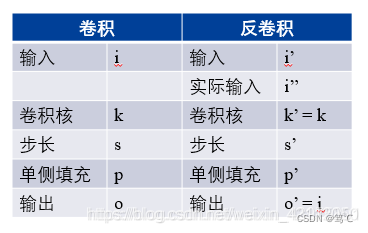
i. 卷积步长s=1时
其中，实际输入 i" 指 s>1 时，对 i’ 中间填0后的尺寸（不包括p’）。
有：反卷积的输出o’即为卷积的输入i；反卷积的核尺寸与卷积的相等。

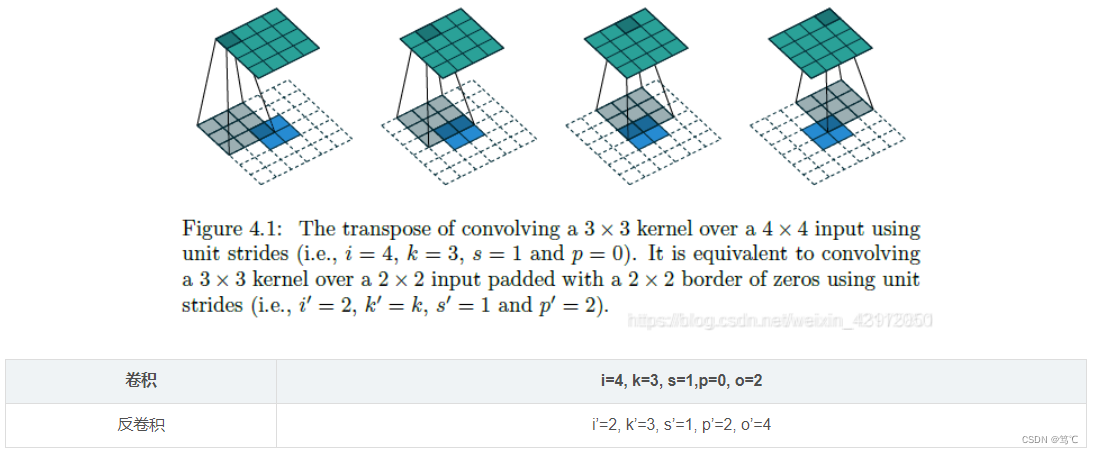
这里解释为什么要在外周填充2层0，即为什么p’=2：
（1）首先，p’=2保证了 o’ = i
（2）这种填充方式，保证了反卷积过程元素位置对应关系，与卷积过程相同。例如：正向卷积过程中，绿色图像左上角的元素，只对蓝色图像左上角元素有贡献。在反卷积时，这样的padding使得，只有蓝色的左上角会影响绿色的左上角数值。
（3）为了保证这种对应关系，有如下结论：p’ = k-p-1
ii. 卷积步长s>1时
直观上，卷积的 s>1 时，反卷积的 s’<1，这也是反卷积又叫 fractionally strided convolutions的原因。
但是不可能真的用非整数的s’做反卷积，为了实现 s’<1：需要在 i’ 每相邻两数间填充 (s-1)个0，填充完后，用 s’=1 的设置进行卷积。
即：（中间填充0）+（s’=1）的组合操作，实现了理论上的 s’ < 1。

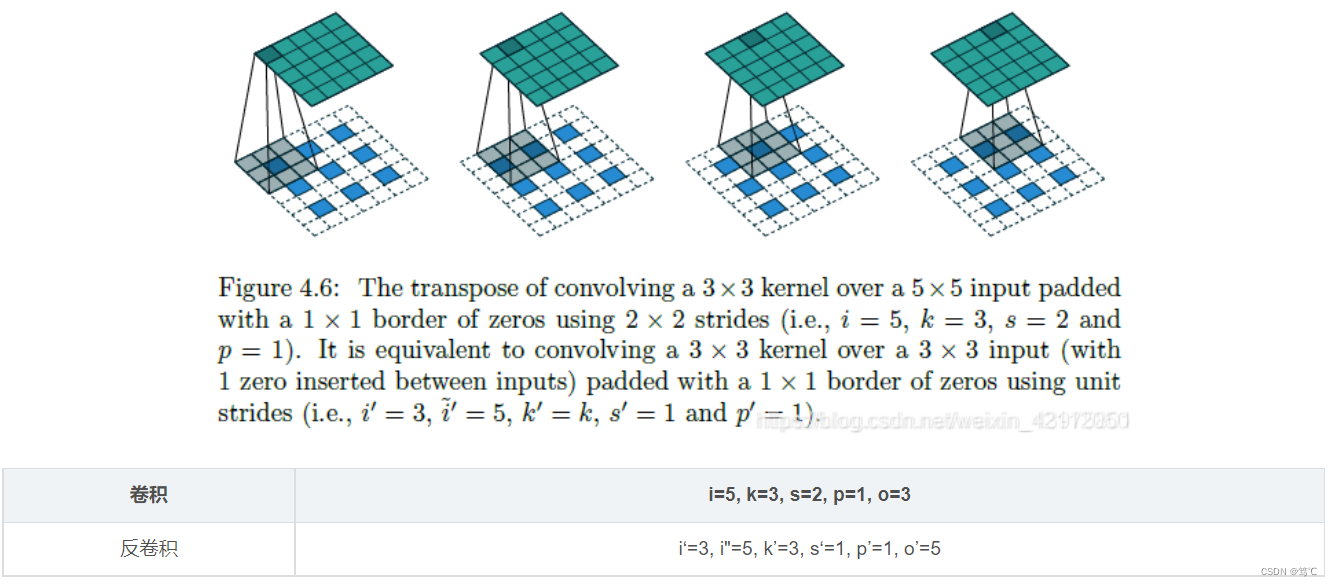
4.2 一般与特殊

4.2.1 一般反卷积的步骤

设对应的卷积参数为：i, k, s, p, o；
目标是：已知 i’ = o，恢复出形状 i，即 o’ = i；
对 i’ 相邻元素间填充（s-1）个0，得到 i" = i’ + (i’-1)(s-1)；
对i’‘进行padding，p’ = k-p-1；
最后进行 k’=k, s’=1 的卷积操作。

4.2.2 卷积 (i+2p-k)/s 无法整除时

在前文中，说明了卷积时，无法整除的情况：a = (i+2p-k)%s
则所有输入为 (i+a), a={0, 1, 2, …, s-1}的图像卷积之后具有相同的输出尺寸。这点在反卷积时需特别注意。
这种卷积所对应的反卷积操作：在一般卷积的第4步之后：在图像右和下侧，填充 a 个0。

设对应的卷积参数为：i, k, s, p, o；
目标是：已知 i’ = o，恢复出形状 i，即 o’ = i；
对 i’ 相邻元素间填充（s-1）个0，得到 i" = i’ + (i’-1)(s-1)；
对i’‘进行padding，p’ = k-p-1；
再在i’'的右和下侧，填充 a 个0；
最后进行 k’=k, s’=1 的卷积操作。

5. 参考

【1】https://blog.csdn.net/weixin_43975801/article/details/104566738
【2】https://zhuanlan.zhihu.com/p/113525131
【3】https://blog.csdn.net/weixin_42112050/article/details/117169004