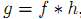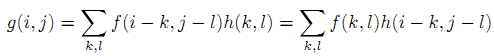本文索引:
文章目录
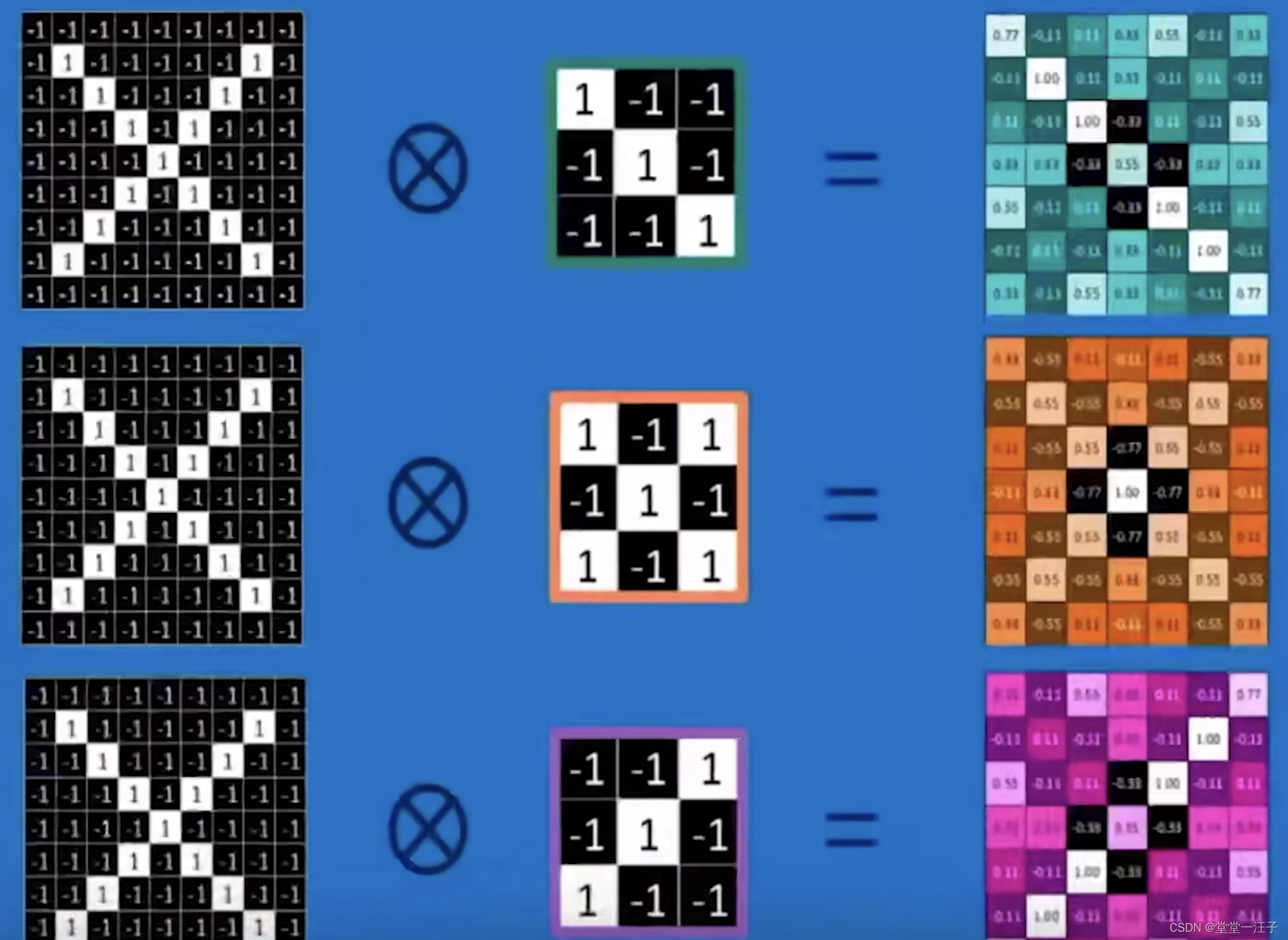
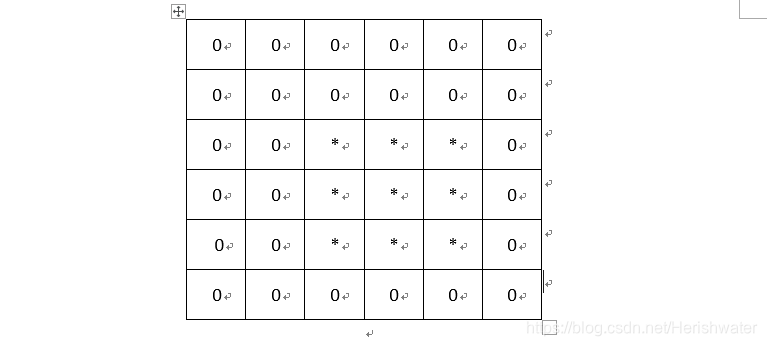
# 一、 什么是卷积? 在图像处理中,卷积操作指的是使用一个卷积核对图像中的每个像素进行一系列操作。 卷积核(算子)是用来做图像处理时的矩阵,图像处理时也称为掩膜,是与原图像做运算的参数。卷积核通常是一个四方形的网格结构(例如3*3的矩阵或像素区域),该区域上每个方格都有一个权重值。 使用卷积进行计算时,需要将卷积核的中心放置在要计算的像素上,一次计算核中每个元素和其覆盖的图像像素值的乘积并求和,得到的结构就是该位置的新像素值。 以下两个算子中演示了具体的卷积计算过程。
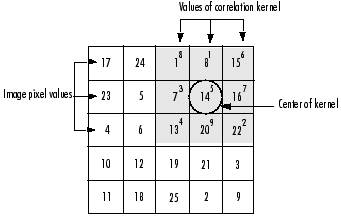
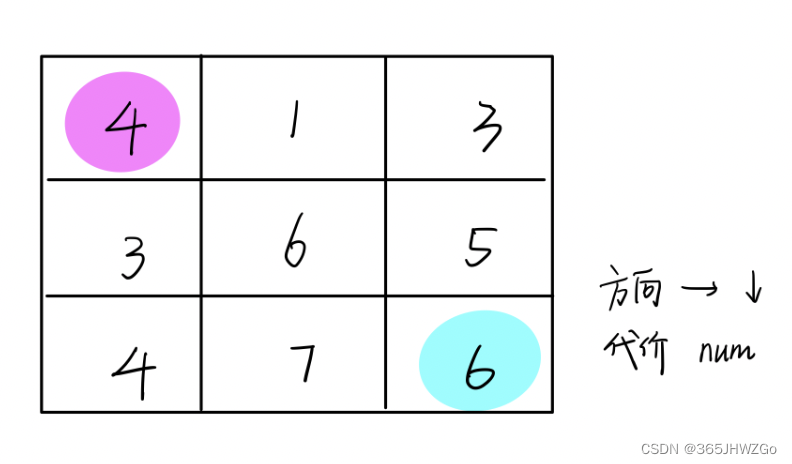
# 二、 相关算子 定义: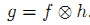 即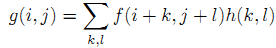,其中h称为相关核(Kernel). 步骤:
- 1)滑动核,使其中心位于输入图像g的(i,j)像素上
- 2)利用上式求和,得到输出图像的(i,j)像素值
- 3)充分上面操纵,直到求出输出图像的所有像素值
【例】
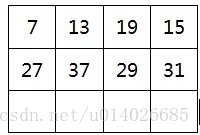
原始像素矩阵为:
\begin{bmatrix}
17 & 24 & 1 & 8 & 15 \
23 & 5 & 7 & 14 & 16 \
4 & 6 & 13 & 20 & 22 \
10 & 12 & 19 & 21 & 3\
11 & 18 & 25 & 2 & 9
\end{bmatrix}
卷积模板h为:
\begin{bmatrix}
8 & 1 & 6 \
3 & 5 & 7 \
4 & 9 & 2
\end{bmatrix}
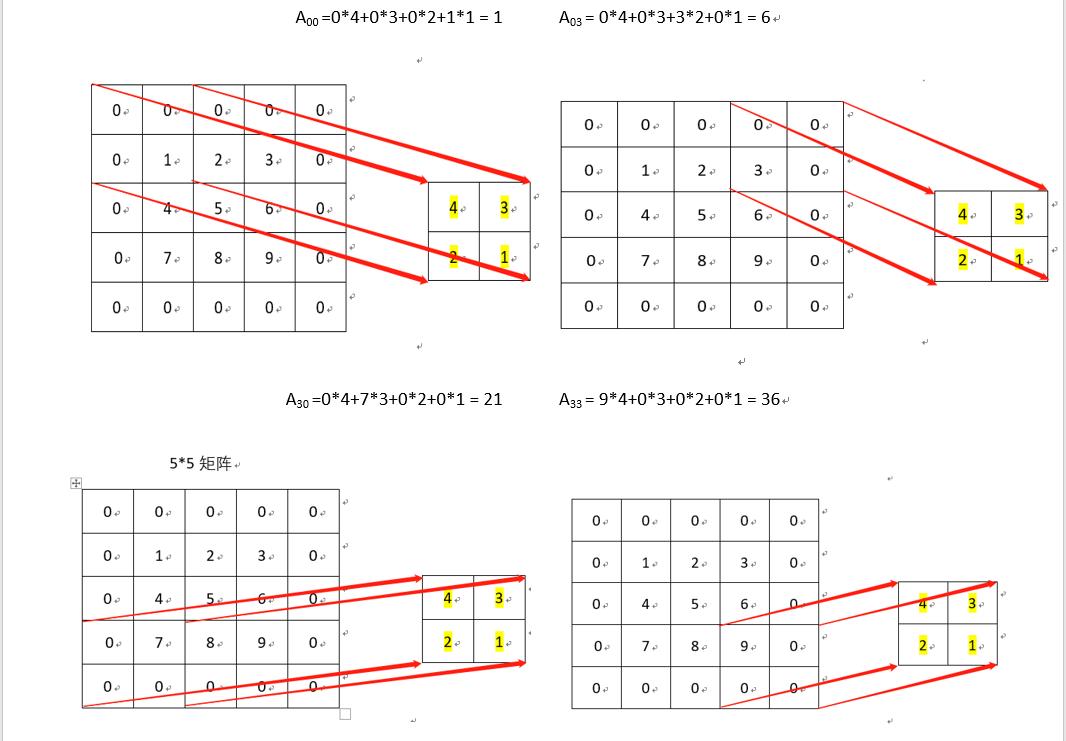
计算输出图像的(2,4)元素=18+81+156+73+145+167+134+209+22*2=585
如图所示:
# 三、 卷积算子
定义:
即
步骤:
- 1)将核围绕中心旋转180度
- 2)滑动核,使其中心位于输入图像g的(i,j)像素上
- 3)利用上式求和,得到输出图像的(i,j)像素值
- 4)充分上面操纵,直到求出输出图像的所有像素值
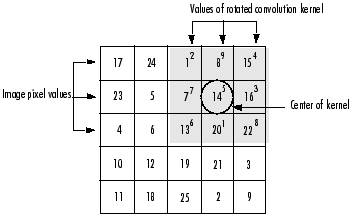
例:计算输出图像的(2,4)元素=12+89+154+77+145+163+136+201+22*8=575
如图所示:
# 四、 边缘效应 当对图像边缘的进行滤波时,核的一部分会位于图像边缘外面。 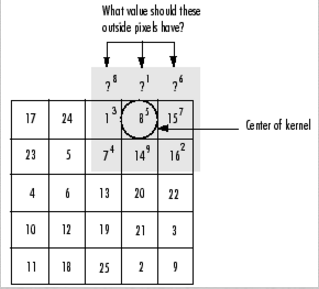 常用的策略包括: - 1)使用常数填充:imfilter默认用0填充,这会造成处理后的图像边缘是黑色的。 - 2)复制边缘像素:I3 = imfilter(I,h,'replicate'); 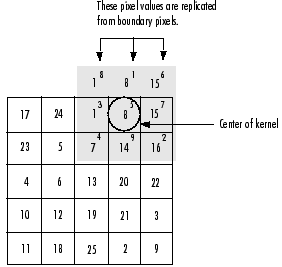
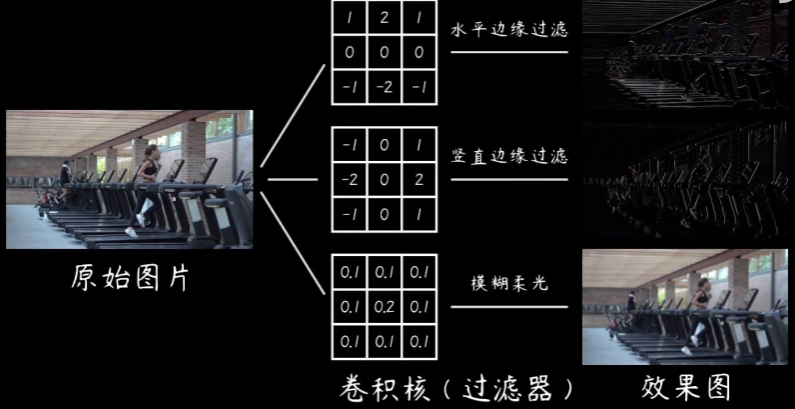
# 五、 常用的卷积核及其用途
-
1)低通滤波器(常用于计算模糊后的效果)\begin{bmatrix}
1/9 & 1/9 & 1/9 \
1/9 & 1/9 & 1/9 \
1/9 & 1/9 & 1/9
\end{bmatrix}
\begin{bmatrix}
1/10 & 1/10 & 1/10 \
1/10 & 2/10 & 1/10 \
1/10 & 1/10 & 1/10
\end{bmatrix}
\begin{bmatrix}
1/16 & 2/16 & 1/16 \
2/16 & 4/16 & 2/16 \
1/16 & 2/16 & 1/16
\end{bmatrix} -
2)高斯滤波器(常用于计算高斯模糊后的效果)
高斯模糊的卷积核也是一个正方形的滤波核,其中每个元素通过以下公式计算得出:
G ( x , y ) = 1 2 π σ 2 ⋅ e x 2 + y 2 2 σ 2 G(x,y)=\frac{1}{2πσ^{2}}·e^{\frac{x^{2}+y^{2}}{2σ^{2}}} G(x,y)=2πσ21⋅e2σ2x2+y2
该公式中σ是标准方差(一般取值为1),x和y分别对应了当前位置到卷积核中心的整数距离。通过这个公式,就可以计算出高斯核中每个位置对应的值。为了保证滤波后的图像不会变暗,需要对高斯核中的权重进行归一化。 -
3)边缘检测(常用于计算图像边缘或者说梯度值)
\begin{bmatrix}
-1 & 0 & -1 \
0 & 4 & 0 \
-1 & 0 & -1
\end{bmatrix}
# 六、 一个例子——使用卷积实现模糊效果 我们将对下面这张图进行模糊处理:  以下为compute shader中关于卷积处理的代码:
[numthreads(32,32,1)]
void Dim_Main (uint3 id : SV_DispatchThreadID)
{float sumR = 0;float sumG = 0;float sumB = 0;float sumA = 0;for (int i = -1; i <= 1; i++) {for (int j = -1; j <= 1; j++) {sumR += texBuffer[(id.x+i)*texWidth[0]+(id.y+j)].r * convolutionTempBuffer[(i+1)*3+(j+1)];sumG += texBuffer[(id.x+i)*texWidth[0]+(id.y+j)].g * convolutionTempBuffer[(i+1)*3+(j+1)];sumB += texBuffer[(id.x+i)*texWidth[0]+(id.y+j)].b * convolutionTempBuffer[(i+1)*3+(j+1)];sumA += texBuffer[(id.x+i)*texWidth[0]+(id.y+j)].a * convolutionTempBuffer[(i+1)*3+(j+1)];}}texBuffer[id.x*texWidth[0]+id.y].r = sumR;texBuffer[id.x*texWidth[0]+id.y].g = sumG;texBuffer[id.x*texWidth[0]+id.y].b = sumB;texBuffer[id.x*texWidth[0]+id.y].a = sumA;Result[id.xy] = float4(sumR, sumG, sumB, sumA);
}
效果如图所示:
图中可以明显的看到左右两边有明显的黑色线条,原图中是没有这样的黑色的,产生这种效果的原因是本文中之前提到过的边缘效应。下面我将修改一部分代码去除边缘效应带来的影响,这里使用的是相邻像素的值方法。
代码如下:
[numthreads(32,32,1)]
void Dim_Main (uint3 id : SV_DispatchThreadID)
{float sumR = 0;float sumG = 0;float sumB = 0;float sumA = 0;for (int i = -1; i <= 1; i++) {for (int j = -1; j <= 1; j++) {if((id.x+i)*texWidth[0]+(id.y+j)>texWidth[0]*texWidth[0]-1){sumR += texBuffer[(id.x+i)*texWidth[0]+(id.y+j)-texWidth[0]].r * convolutionTempBuffer[(i+1)*3+(j+1)];sumG += texBuffer[(id.x+i)*texWidth[0]+(id.y+j)-texWidth[0]].g * convolutionTempBuffer[(i+1)*3+(j+1)];sumB += texBuffer[(id.x+i)*texWidth[0]+(id.y+j)-texWidth[0]].b * convolutionTempBuffer[(i+1)*3+(j+1)];sumA += texBuffer[(id.x+i)*texWidth[0]+(id.y+j)-texWidth[0]].a * convolutionTempBuffer[(i+1)*3+(j+1)];}sumR += texBuffer[(id.x+i)*texWidth[0]+(id.y+j)].r * convolutionTempBuffer[(i+1)*3+(j+1)];sumG += texBuffer[(id.x+i)*texWidth[0]+(id.y+j)].g * convolutionTempBuffer[(i+1)*3+(j+1)];sumB += texBuffer[(id.x+i)*texWidth[0]+(id.y+j)].b * convolutionTempBuffer[(i+1)*3+(j+1)];sumA += texBuffer[(id.x+i)*texWidth[0]+(id.y+j)].a * convolutionTempBuffer[(i+1)*3+(j+1)];}}texBuffer[id.x*texWidth[0]+id.y].r = sumR;texBuffer[id.x*texWidth[0]+id.y].g = sumG;texBuffer[id.x*texWidth[0]+id.y].b = sumB;texBuffer[id.x*texWidth[0]+id.y].a = sumA;Result[id.xy] = float4(sumR, sumG, sumB, sumA);
}
效果如图所示:
可以看到,图中左边的黑色线条已经被滤除,右边也可以采用类似的方法来剔除。实际使用中,也可以根据情况使用纯色来做剔除,这样可以节省部分效率,如下图中我使用的是纯白色来剔除边缘效应。