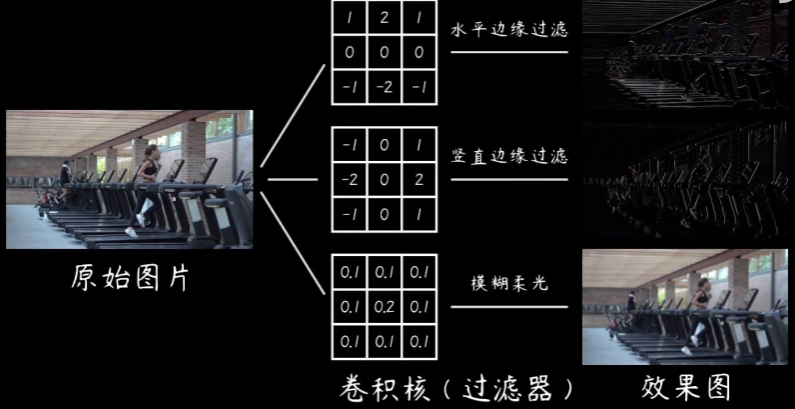
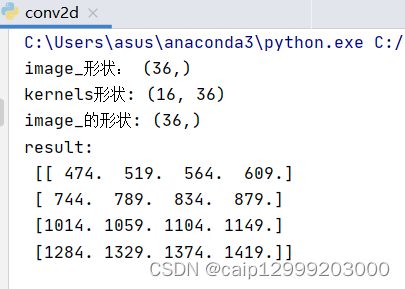
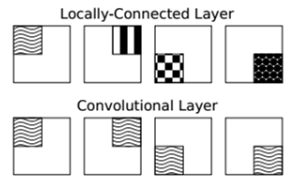
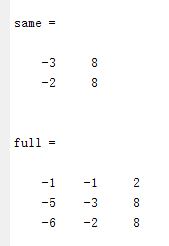之前，习惯把记录和总结的知识点放到云笔记上，但发现CSDN这个博客注册好久了，但却没有往上面放文章，所以决定把以前的笔记整理一下，放到这里来，以便交流学习。

关于信号的卷积

最初认识卷积来源于《信号与系统》这门课，到现在对这块还是逻辑上认可，直观上迷茫的状态，重新学习一下，简单总结如下：

还是从《信号与系统》里的知识开始讲起，单位冲激信号$\delta(n)$仅在$n$=0时，取得值1，其他位置皆为0。$\delta(n)$是一类最简单的信号，我们可以将任意一个复杂的信号分解为多个类似$\delta(n)$这样简单的信号。例如，对于一个任意的离散信号$x(n)$，如下图(a)所示，当$n=k$时，其取值为$x(k)$，用单位冲激信号来表示的话，可写为：

$$x(k) = x(k)\delta(n-k)=x(n)\delta(n-k)$$

式中，$\delta(n-k)$表示单位冲激信号的延时，如图b。这样，将$s(n)$与$\delta(n-k)$相乘之后，所得到的的信号除了在$n=k$处取值为$x(k)$而不为零外，其他各点均为零。

如果重复对$x(n)$和$\delta(n-m)$相乘，其中m是另一个延时($m\not=k$)，则所得到的的信号仅在$n=m$时不为零，其值为$x(m)$，而在其余各处均为零。这说明，信号$x(n)$与单位冲激信号的某个延时$\delta(n-m)$相乘，实际上就是将信号$x(n)$在$n=m$处的单个值$x(m)$挑选出来。因此，如果在所有可能的延时处，即$-\infty<m<\infty$，都重复这样的动作，然后把得到的结果相加，即可得到$x(n)$的另外一种表达式：

$$x(n)=\sum_{m=-\infty}^{\infty}x(m)\delta(n-m)$$

这样，就将任意的一个信号分解为多个冲激信号的叠加。

单位冲激响应是输入信号为单位冲激信号$\delta(n)$时所对应的系统输出，常用$h(n)$来表示。对于线程时不变系统，如果知道了单位冲激信号的输出，根据叠加定理，就可知道任意复杂信号的输出。可得：

$$y(n)=\sum_{m=-\infty}^{\infty}x(m)h(n-m)$$

上式就是即为线性卷积，通常称为卷积，可以简写为：$y(n)=x(n)*h(n)$

对于连续信号，同理，任意信号可用冲激信号的组合表示，由冲激响应$h(t)$可得：

$$y(t)=\int_{-\infty}^{\infty}x(\tau)h(t-\tau)d\tau$$

卷积方法的原理就是将信号分解为冲激信号之和。

数学上的卷积

卷积是分析数学中一种重要的运算。设： ${\displaystyle f(x)} , {\displaystyle g(x)} 是 {\displaystyle \mathbb {R} }$ 上的两个可积函数，作积分：

$$\int_{-\infty}^{\infty}f(\tau)g(x-\tau)d\tau$$

可以证明，对于所有$x\in(-\infty,+\infty)$，上述积分都是存在的。这样，随着${\displaystyle x}$的不同取值，这个积分就定义了一个新函数${\displaystyle h(x)}$，称为函数 $f$ 与 $g$ 的卷积，记为$h(x)=(f*g)(x)$。可以验证$(g*f)(x)=(f*g)(x)$，且$h(x)$仍为可积函数。

在泛函分析中，卷积是通过两个函数$f$和$g$生成第三个函数的一种数学算子，表征函数$f$与经过翻转和平移的$g$的乘积函数所围成的的曲边梯形的面积。

图示两个方形脉冲波的卷积。其中函数”$g$”首先对$\tau =0$翻转，接着平移”$t$”，成为$g(t-\tau )$。那么重叠部分的面积就相当于”$t$”处的卷积，其中横坐标代表待变量$\tau$以及新函数$f\ast g$的自变量”$t$”。

图示方形脉冲波和指数衰退的脉冲波的卷积（后者可能出现于RC电路中），同样地重叠部分面积就相当于”$t$”处的卷积。注意到因为”$g$”是对称的，所以在这两张图中，反射并不会改变它的形状。

上图中，第一行分别代表两个函数$f(t)$和$g(t)$。将两个函数都用$\tau$来表示，从而得到了$f(\tau)$和$g(\tau)$。将函数$g(\tau)$关于$\tau=0$翻转，得到$g(-\tau)$，然后将$g(-\tau)$平移$t$个单位，得到$g(t-\tau)$，对应第二行图像。由于$t$为非常数(实际上是时间变量)，当时间变量(以下简称“时移”)取不同值时，$g(t-\tau )$能沿着$\tau$轴“滑动“，第三四五行可理解为“滑动”。让t从$-\infty$滑动到$+\infty$。两函数交会时，交会范围中两函数乘积的积分值即为$f(x)$和$g(x)$的卷积。换句话说，计算一个滑动的的加权平均值。也就是使用$g(-\tau )$当做加权函数，来对$f(\tau)$取加权平均值。

如何通俗易懂的理解卷积

知乎里面有一个关于如何理解卷积的话题，如何通俗易懂的理解卷积。

以上，部分内容来源于维基百科。