2.如果矩阵的中心在边缘就要将原矩阵进行扩展,例如补0
3.卷积的计算步骤:
(1)
(2)
(3)
(4)
full 是用旋转后的核的从角开始对应。
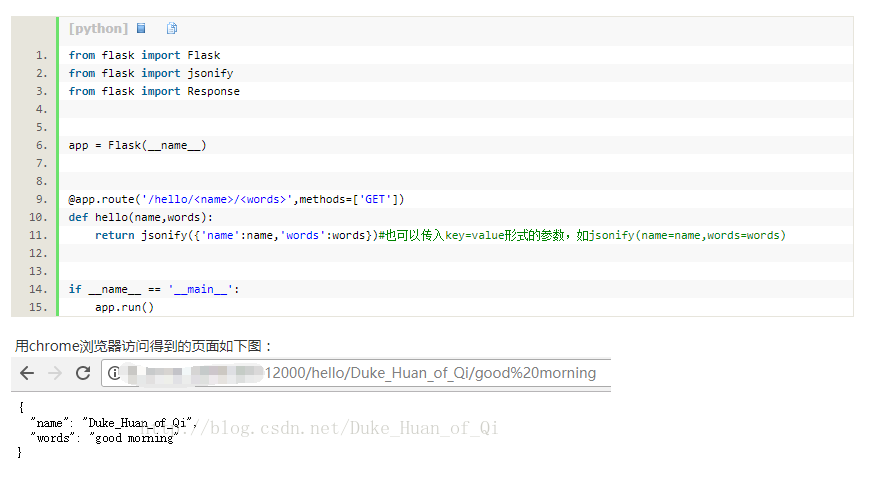
MATALB仿真结果
a =
b =
same:
c =
full:
d =
4 卷积在具体学科中的应用
图像处理:用一个模板和一幅图像进行卷积,对于图像上的一个点,让模板的原点和该点重合,然后模板上的点和图像上对应的点相乘,然后各点的积相加,就得到了该点的卷积值。对图像上的每个点都这样处理。由于大多数模板都是对称的,所以模板不旋转。卷积是一种积分运算,用来求两个曲线重叠区域面积。可以看作加权求和,可以用来消除噪声、特征增强。
把一个点的像素值用它周围的点的像素值的加权平均代替。
卷积是一种线性运算,图像处理中常见的mask运算都是卷积,广泛应用于图像滤波。
卷积在数据处理中用来平滑,卷积有平滑效应和展宽效应.
电路学:卷积法的原理是根据线性定常电路的性质(齐次性、叠加性、时不变性、积分性等),借助电路的单位冲激响应h(t),求解系统响应的工具,系统的激励一般都可以表示为冲击函数和激励的函数的卷积,而卷积为高等数学中的积分概念。概念中冲击函数的幅度是由每个矩形微元的面积决定的。
卷积关系最重要的一种情况,就是在信号与线性系统或数字信号处理中的卷积定理。利用该定理,可以将时间域或空间域中的卷积运算等价为频率域的相乘运算,从而利用FFT等快速算法,实现有效的计算,节省运算代价。
信号处理:
1)卷积实质上是对信号进行滤波;
2)卷积就是用冲击函数表示激励函数,然后根据冲击响应求解系统的零状态响应。
卷积是求和(积分)。对于线性时不变的系统,输入可以分解成很多强度不同的冲激的和的形式(对于时域就是积分),那么输出也就是这些冲激分别作用到系统产生的响应的和(或者积分)。所以卷积的物理意义就是表达了时域中输入,系统冲激响应,以及输出之间的关系。
信号角度:卷积代表了线性系统对输入信号的响应方式,其输出就等于系统冲击函数和信号输入的卷积,只有符合叠加原理的系统,才有系统冲击函数的概念,从而卷积成为系统对输入在数学上运算的必然形式,冲击函数实际上是该问题的格林函数解。点激励源作为强加激励,求解某个线性问题的解,得到的格林函数即是系统冲击响应.所以在线性系统中,系统冲击响应与卷积存在着必然的联系。
数学:来说卷积就是定义两个函数的一种乘法,或者是一种反映两个序列或函数之间的运算方法。对离散序列来说就是两个多项式的乘法。物理意义就是冲激响应的线性叠加,所谓冲激响应可以看作是一个函数,另一个函数按冲激信号正交展开。
在现实中:卷积代表的是将一种信号搬移到另一频率中,比如调制,这是频率卷。
物理:卷积可代表某种系统对某个物理量或输入的调制或污染。
在现实中:卷积代表的是将一种信号搬移到另一频率中,比如调制,这是频率卷。
形象比喻:卷积我觉得就象一把锉刀,它主要是把一些非光滑的函数或算子光滑化。
信号处理的任务就是寻找和信号集合对应的一个集合,然后在另外一个集合中分析信号,Fourier变换就是一种,它建立了时域中每个信号函数与频域中的每个频谱函数的一一对应关系,这是元素之间的对应。那么运算之间的对应呢,在时域的加法对应频域中的加法,这就是FT线性性的体现;那么时域的乘法对应什么呢,最后得到的那个表达式我们就把它叫卷积,就是对应的频域的卷积。
简单来说,卷积是一种重叠关系,也就是说,所得到的结果反映了两个卷积函数的重叠部分。所以,用一个已知频段的函数卷积另一个频段很宽的函数,也就是对后者进行了滤波,后者跟前者重叠的频段才能很好地通过这个filter.
5 卷积与多项式
信号处理中的一个重要运算是卷积.初学卷积的时候,往往是在连续的情形,两个函数f(x),g(x)的卷积,是∫f(u)g(x-u)du。当然,证明卷积的一些性质并不困难,比如交换,结合等等,但是对于卷积运算的来处,初学者就不甚了了。
其实,从离散的情形看卷积,或许更加清楚,对于两个序列f[n],g[n],一般可以将其卷积定义为s[x]= ∑f[k]g[x-k]。
卷积的一个典型例子,其实就是初中就学过的多项式相乘的运算。
比如(x*x+3*x+2)(2*x+5)一般计算顺序如下:
(x*x+3*x+2)(2*x+5)
= (x*x+3*x+2)*2*x+(x*x+3*x+2)*5
= 2*x*x*x+3*2*x*x+2*2*x+ 5*x*x+3*5*x+10
然后合并同类项的系数,
2x*x*x
3*2+1*5x*x
2*2+3*5x
2*5
2*x*x*x+11*x*x+19*x+10
实际上,从线性代数可以知道,多项式构成一个向量空间,其基底可选为{1,x,x*x,x*x*x,...}如此,则任何多项式均可与无穷维空间中的一个坐标向量相对应,如,(x*x+3*x+2)对应于(1 3 2),(2*x+5)对应于(2,5)。线性空间中没有定义两个向量间的卷积运算,而只有加法、数乘两种运算,而实际上,多项式的乘法,就无法在线性空间中说明,可见线性空间的理论多么局限了。但如果按照我们上面对向量卷积的定义来处理坐标向量,(1 3 2)*(2 5)则有(1 3 2)*(2 5)=(2 11 19 10)。
回到多项式的表示上来,(x*x+3*x+2)(2*x+5)=2*x*x*x+11*x*x+19*x+10,结果跟我们用传统办法得到的是完全一样的.换句话,多项式相乘,相当于系数向量的卷积.其实道理也很简单,卷积运算实际上是分别求 x*x*x ,x*x,x,1的系数,也就是说,他把加法和求和杂合在一起做了。(传统的办法是先做乘法,然后在合并同类项的时候才作加法)以x*x的系数为例,得到x*x,或者是用x*x乘5,或者是用3x乘2x,也就是
2 3 1
_ 2 5
6+5=11
其实,这正是向量的内积.如此则,卷积运算,可以看作是一串内积运算.既然是一串内积运算,则我们可以试图用矩阵表示上述过程。
[ 2 3 1 0 0 0]
[ 0 2 3 1 0 0]==A
[ 0 0 2 3 1 0]
[ 0 0 0 2 3 1]
[0 0 2 5 0 0]' == x
b= Ax=[ 2 11 19 10]'
采用行的观点看Ax,则b的每行都是一个内积。A的每一行都是序列[23 1]的一个移动位置。显然,在这个特定的背景下,我们知道,卷积满足交换,结合等定律,因为,众所周知的,多项式的乘法满足交换律,结合律.在一般情形下,其实也成立.
在这里,我们发现多项式,除了构成特定的线性空间外,基与基之间还存在某种特殊的联系,正是这种联系,给予多项式空间以特殊的性质.
在学向量的时候,一般都会举这个例子,甲有三个苹果,5个橘子,乙有5个苹果,三个橘子,则共有几个苹果,橘子。老师反复告诫,橘子就是橘子,苹果就是苹果,可不能混在一起。所以有(3,5)+(5,3)=(8,8).是的,橘子和苹果无论怎么加,都不会出什么问题的,但是,如果考虑橘子乘橘子,或者橘子乘苹果,这问题就不大容易说清了。
又如复数,如果仅仅定义复数为数对(a,b),仅仅在线性空间的层面看待C2,那就未免太简单了。实际上,只要加上一条(a,b)*(c,d)=(ac-bd,ad+bc)。则情况马上改观,复变函数的内容多么丰富多彩,是众所周知的。另外,回想信号处理里面的一条基本定理,频率域的乘积,相当于时域或空域信号的卷积.恰好和这里的情形完全对等.这后面存在什么样的隐态联系,需要继续参详.
从这里看,高等的卷积运算其实不过是一种初等的运算的抽象而已.中学学过的数学里面,其实还蕴涵着许多高深的内容(比如交换代数)。温故而知新,斯言不谬.其实这道理一点也不复杂,人类繁衍了多少万年了,但过去n多年,人们只知道男女媾精,乃能繁衍后代。精子,卵子的发现,生殖机制的研究,也就是最近多少年的事情。
孔子说,道在人伦日用中,看来我们应该多用审视的眼光看待周围,乃至自身,才能知其然,而知其所以然。