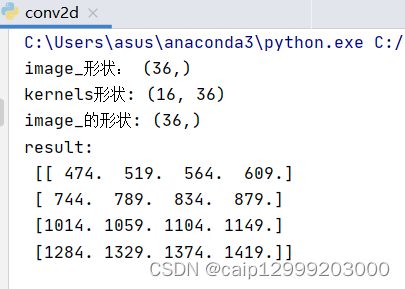
昨天立下flag,要开始学习深度学习,深度学习中十分重要的就是卷积神经网络,顾名思义,卷积神经网络中一定会用到卷积。喵哥在博友的一篇博文中看到卷积运算用于图像边缘检测的应用实例,博友十分细心的在截图上做了卷积的运算过程,手动点赞。喵哥最近在看傅里叶变换(连续),对卷积还算记得起一点,但是对图像这种矩阵的卷积运算,的确是没有太多影响,本科学的图像处理的课程真是全部还给老师了。本着勤奋好学的理念,在网上搜了几篇关于矩阵卷积运算的介绍,收获颇丰。但是在看教程时也发现一些小错误和容易引起误会的地方,所以写下这篇博文作为一个日后复习的好去处。
设有矩阵A,B,两者之间的卷积结果可以用公式:
表示。以上公式表示的是从0开始计数,这不同于MATLAB的从1开始计数,所以公式与MATLAB提供的卷积公式稍有形式上的差异。同一维的数据卷积一样——把卷积模板翻转180°,然后从上至下,从左到右滑动模板,然后计算模板与原始图像交集元素的乘积和,得到的即是卷积后的数值。
假设B是模板,A是原始图像,那么用一组矩形相交关系来表示A,B移动的状态。










这些相交方式的一些集合就构成了各种卷积定义的运算模式。在MATLAB中有三种二维的矩阵卷积定义:valid、same和full。MATLAB对他们的解释为:
'valid'
Returns only those parts of the convolution that are computed without the zero-padded edges. Using this option, size(C) = max([ma-max(0,mb-1),na-max(0,nb-1)],0).'same'
Returns the central part of the convolution of the same size as A.'full'
Returns the full two-dimensional convolution (default).假设,
。
在计算卷积A*B时,需要先把B做翻转,得到
,然后把这个翻转的矩阵在大矩阵A中移动。
valid型卷积
valid类型的卷积只考虑B包含于A的情况(即情况5),在矩阵A外围完全不需要补0。若B移动的步长是1,最终的卷积结果的矩阵大小为nc(A) - nc(B) + 1,nc(A),nc(B)分别为A,B矩阵的边长。
| 1*9 | 2*8 | 3*7 | 4 | 5 | 6 |
| 2*6 | 3*5 | 4*4 | 5 | 6 | 7 |
| 3*3 | 4*2 | 5*1 | 6 | 7 | 8 |
| 4 | 5 | 6 | 7 | 8 | 9 |
| 5 | 6 | 7 | 8 | 9 | 10 |
| 6 | 7 | 8 | 9 | 10 | 11 |
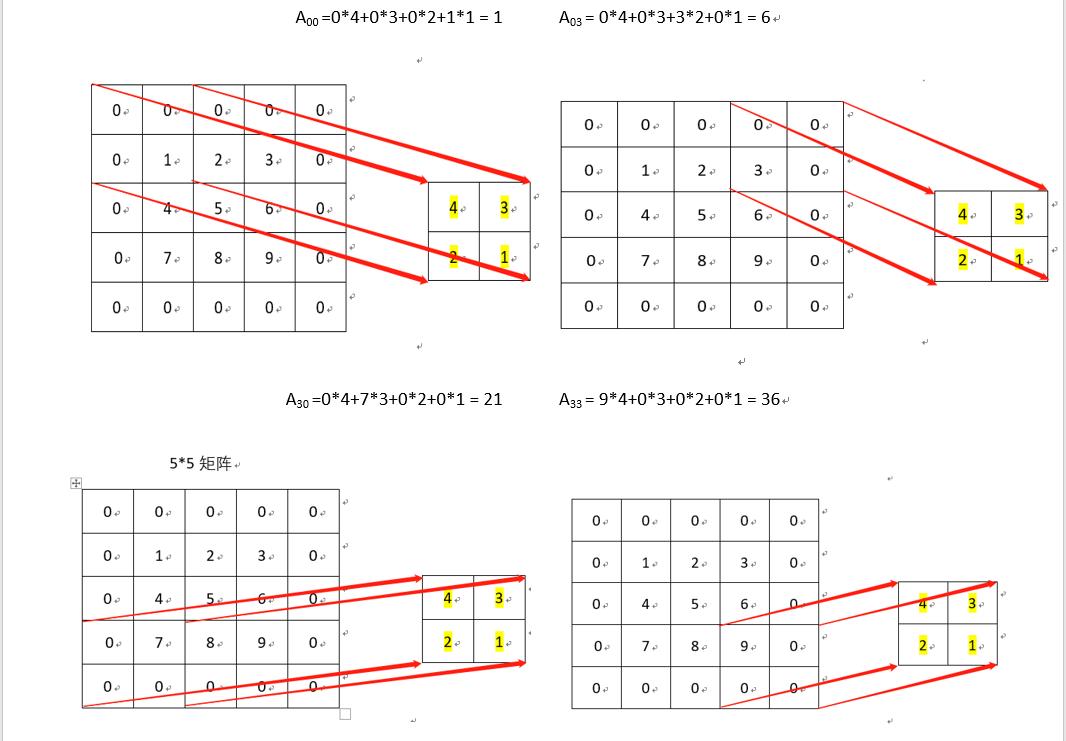
第一个重叠区域的乘积计算,得到的值是111,依次计算得到的卷积矩阵为
same型卷积
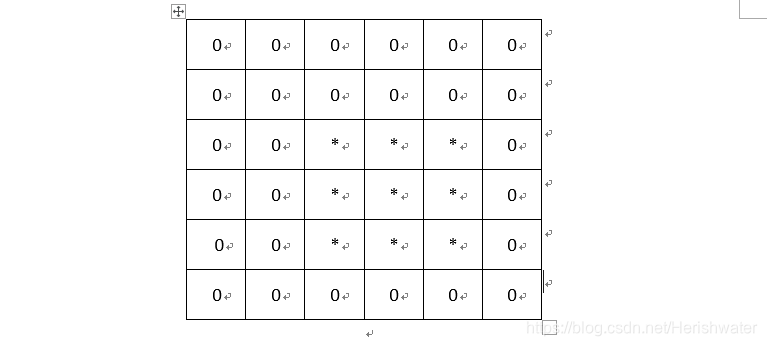
这个类型的卷积在valid的基础上,还要包含小矩阵交于大矩阵的右边缘、下边缘以及右下角重叠的情况(7,9,10)。给A矩阵的右边缘和下边缘补0,这样计算出卷积的矩阵与矩阵A的大小一致。
full型卷积
这是包含所有重叠情况的卷积类型,即除了第一种分离状态的所有情况,需要在A矩阵四周补0。这样得出的卷积矩阵比A矩阵长2个元素。