目录:
- 5.1 函数的定义与使用
- 5.2 实例7: 七段数码管绘制
- 5.3 代码复用与函数递归
- 5.4模块4: PyInstaller库的使用
- 5.5实例8: 科赫雪花小包裹
导学
前课复习
数字类型及操作:
- 整数类型的无限范围及4种进制表示
- 浮点数类型的近似无限范围、小尾数及科学计数法
- +、-、*、/、//、%、**、二元增强赋值操作符
- abs()、divmod()、pow()、round()、max()、min()
- int()、float()、complex()
for…in…(计算思维):
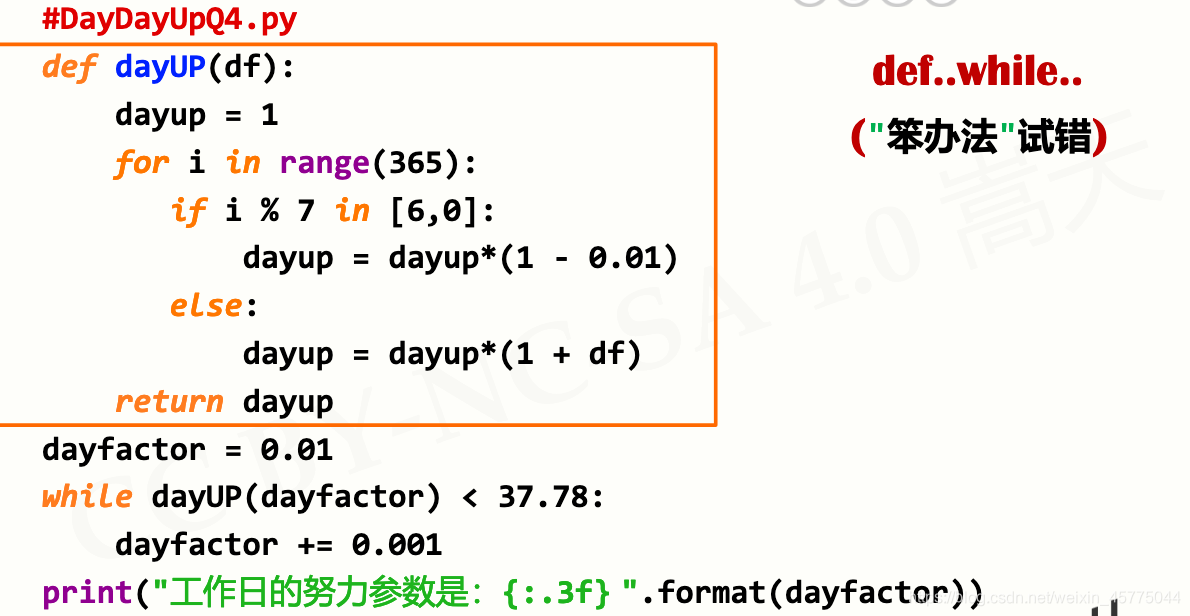
def…while…("笨办法"试错)
字符串类型及操作
- 正向递增序号、反向递减序号、<字符串>[M:N:K]
- +、*、len()、str()、hex()、oct()、ord()、chr()
- .lower()、.upper()、.split()、.count()、.replace()
- .center()、.strip()、.join()、.format()格式化

程序的分支结构
- 单分支if 二分支if-else 及紧凑形式
- 多分支if-elif-else 及条件之间关系
- not and or > >= == <= < !=
- 异常处理try-except-else-finally
程序的循环结构
- for…in遍历循环: 计数、字符串、列表、文件…
- while无限循环
- continue和break保留字: 退出当前循环层次
- 循环else的高级用法: 与break有关

本课概要
- 5.1 函数的定义与使用
- 5.2 实例7: 七段数码管绘制
- 5.3 代码复用与函数递归
- 5.4模块4: PyInstaller库的使用
- 5.5实例8: 科赫雪花小包裹
方法论- Python基本代码抽象即函数的使用方法
实践能力-学会编写带有函数并复用代码的程序
练习(可选)- 5道编程@Python123
测验- 10道单选+2道编程@Python123
- 5.1 函数的定义与使用
目录:
- 函数的理解与定义
- 函数的使用及调用过程
- 函数的参数传递
- 函数的返回值
- 局部变量和全局变量
- lambda函数
小结:
- 使用保留字def定义函数,lambda定义匿名函数
- 可选参数(赋初值)、可变参数(*b)、名称传递
- 保留字return可以返回任意多个结果
- 保留字global声明使用全局变量,一些隐式规则
5.1.1- 函数的理解与定义
函数的定义:
函数是一段代码的表示
- 函数是一段具有特定功能的、可重用的语句组
- 函数是一种功能的抽象,一般函数表达特定功能
- 两个作用:降低编程难度和代码复用


y = f(x)
- 函数定义时,所指定的参数是一种占位符
- 函数定义后,如果不经过调用,不会被执行
- 函数定义时,参数是输入、函数体是处理、结果是输出(IPO)
5.1.2- 函数的使用及调用过程
函数的调用:
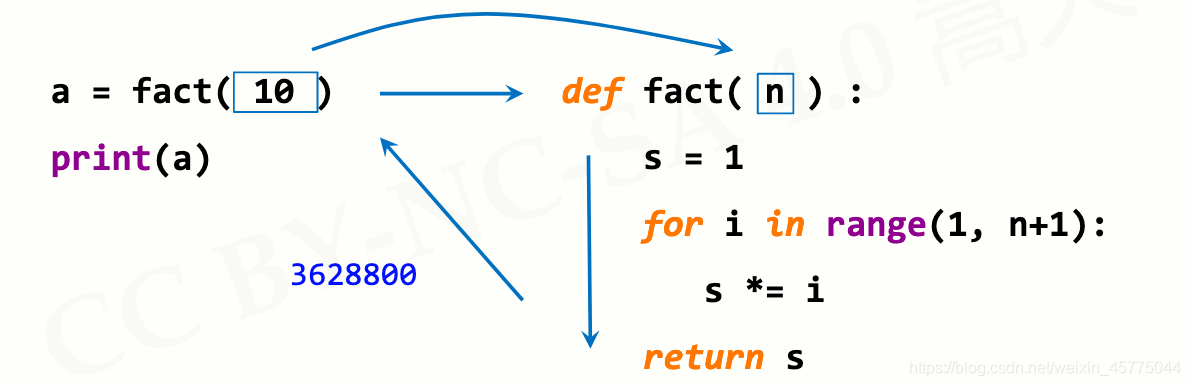
调用是运行函数代码的方式

函数的调用过程:
5.1.3- 函数的参数传递
参数个数:
函数可以有参数,也可以没有,但必须保留括号

可选参数传递:
函数定义时可以为某些参数指定默认值,构成可选参数


函数定义时可以设计可变数量参数,既不确定参数总数量


参数传递的两种方式:
函数调用时,参数可以按照位置或名称方式传递

5.1.4- 函数的返回值
函数可以返回0个或多个结果
- return保留字用来传递返回值
- 函数可以有返回值,也可以没有,可以有return,也可以没有
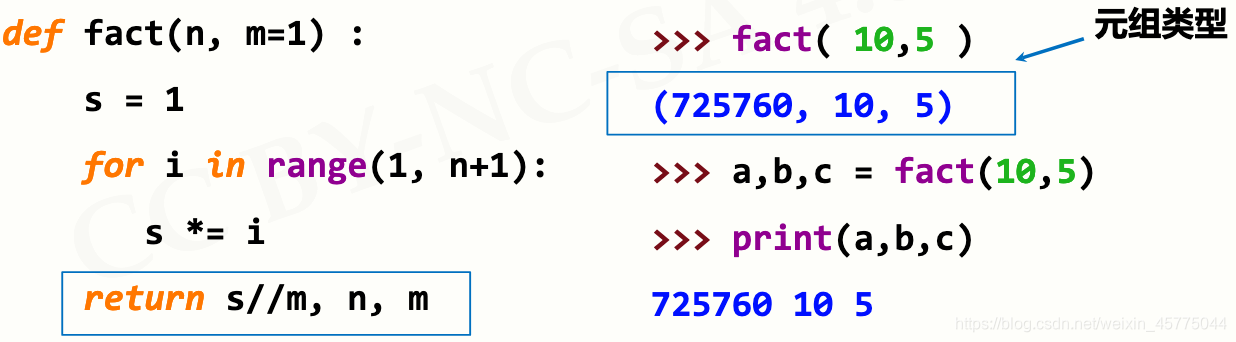
- return可以传递0个返回值,也可以传递任意多个返回值
函数调用时,参数可以按照位置或名称方式传递
5.1.5- 局部变量和全局变量


规则1: 局部变量和全局变量是不同变量
- 局部变量是函数内部的占位符,与全局变量可能重名但不同
- 函数运算结束后,局部变量被释放
- 可以使用global保留字在函数内部使用全局变量


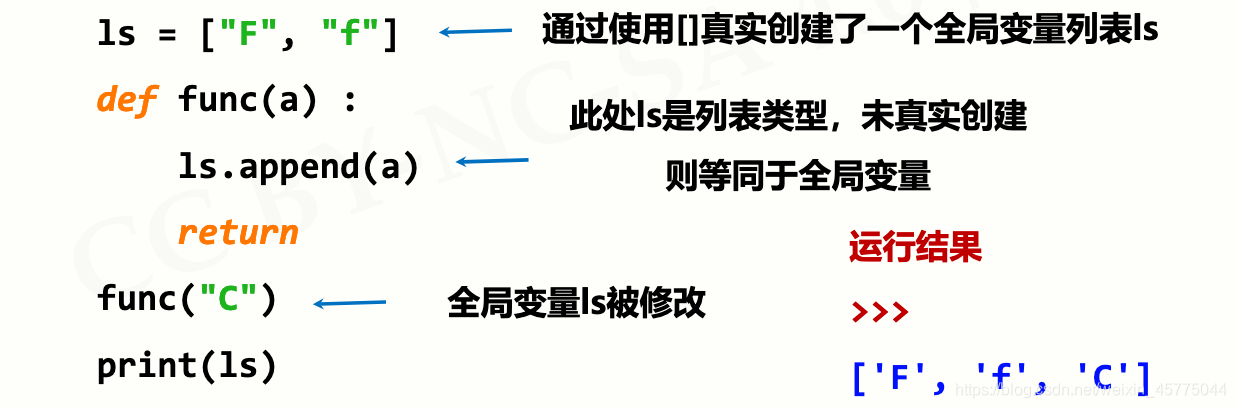
规则2: 局部变量为组合数据类型且未创建,等同于全局变量

使用规则
- 基本数据类型,无论是否重名,局部变量与全局变量不同
- 可以通过global保留字在函数内部声明全局变量
- 组合数据类型,如果局部变量未真实创建,则是全局变量
5.1.6- lambda函数
lambda函数:
lambda函数返回函数名作为结果
- lambda函数是一种匿名函数,即没有名字的函数
- 使用lambda保留字定义,函数名是返回结果
- lambda函数用于定义简单的、能够在一行内表示的函数


lambda函数的应用
谨慎使用lambda函数
- lambda函数主要用作一些特定函数或方法的参数
- lambda函数有一些固定使用方式,建议逐步掌握
- 一般情况,建议使用def定义的普通函数
- 5.2 实例7: 七段数码管绘制
5.2.1 问题分析

七段数码管绘制
- 需求:用程序绘制七段数码管,似乎很有趣
- 该怎么做呢?
turtle绘图体系➡️七段数码管绘制

5.2.2 实例讲解(上)
七段数码管绘制
基本思路
- 步骤1:绘制单个数字对应的数码管
- 步骤2:获得一串数字,绘制对应的数码管
- 步骤3:获得当前系统时间,绘制对应的数码管
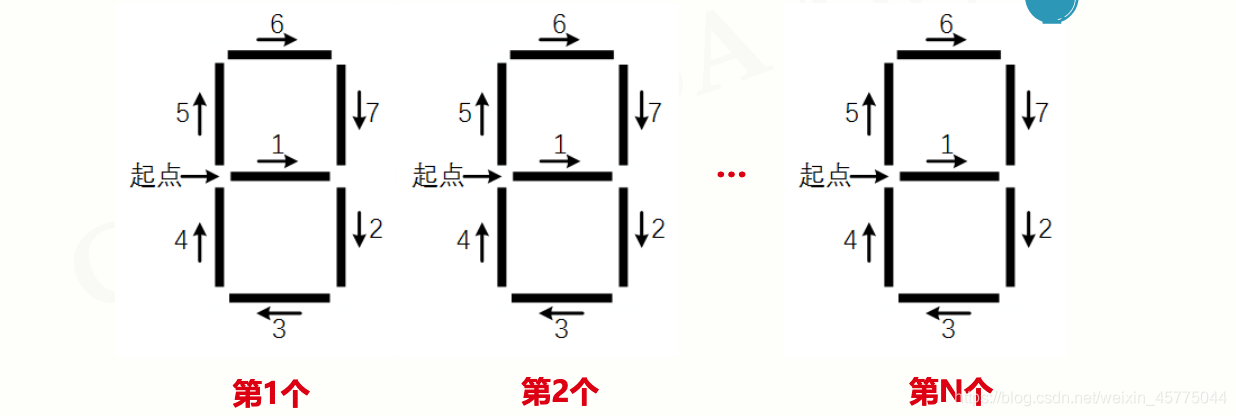
步骤1: 绘制单个数码管
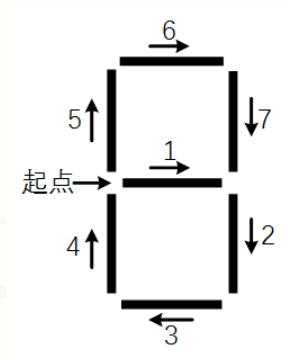
- 七段数码管由7个基本线条组成
- 七段数码管可以有固定顺序
- 不同数字显示不同的线条
#SevenDigitsDrawV1.py
import turtle
def drawLine(draw): #绘制单段数码管turtle.pendown() if draw else turtle.penup()turtle.fd(40)turtle.right(90)
def drawDigit(digit): #根据数字绘制七段数码管drawLine(True) if digit in [2,3,4,5,6,8,9] else drawLine(False)drawLine(True) if digit in [0,1,3,4,5,6,7,8,9] else drawLine(False)drawLine(True) if digit in [0,2,3,5,6,8,9] else drawLine(False)drawLine(True) if digit in [0,2,6,8] else drawLine(False)turtle.left(90)drawLine(True) if digit in [0,4,5,6,8,9] else drawLine(False)drawLine(True) if digit in [0,2,3,5,6,7,8,9] else drawLine(False)drawLine(True) if digit in [0,1,2,3,4,7,8,9] else drawLine(False)turtle.left(180)turtle.penup()turtle.fd(20)
def drawDate(date): #获得要输出的数字for i in date:drawDigit(eval(i)) #通过eval()函数将数字变为整数
def main():turtle.setup(800, 350, 200, 200)turtle.penup()turtle.fd(-300)turtle.pensize(5)drawDate('20181010')turtle.hideturtle()turtle.done()
main()
步骤2: 获取一段数字,绘制多个数码管
#SevenDigitsDrawV2.py
import turtle, time
def drawGap(): #绘制数码管间隔turtle.penup()turtle.fd(5)
def drawLine(draw): #绘制单段数码管drawGap()turtle.pendown() if draw else turtle.penup()turtle.fd(40)drawGap()turtle.right(90)
def drawDigit(d): #根据数字绘制七段数码管drawLine(True) if d in [2,3,4,5,6,8,9] else drawLine(False)drawLine(True) if d in [0,1,3,4,5,6,7,8,9] else drawLine(False)drawLine(True) if d in [0,2,3,5,6,8,9] else drawLine(False)drawLine(True) if d in [0,2,6,8] else drawLine(False)turtle.left(90)drawLine(True) if d in [0,4,5,6,8,9] else drawLine(False)drawLine(True) if d in [0,2,3,5,6,7,8,9] else drawLine(False)drawLine(True) if d in [0,1,2,3,4,7,8,9] else drawLine(False)turtle.left(180)turtle.penup()turtle.fd(20)
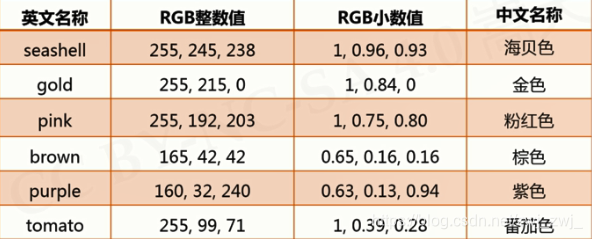
def drawDate(date):turtle.pencolor("red")for i in date:if i == '-':turtle.write('年',font=("Arial", 18, "normal"))turtle.pencolor("green")turtle.fd(40)elif i == '=':turtle.write('月',font=("Arial", 18, "normal"))turtle.pencolor("blue")turtle.fd(40)elif i == '+':turtle.write('日',font=("Arial", 18, "normal"))else:drawDigit(eval(i))
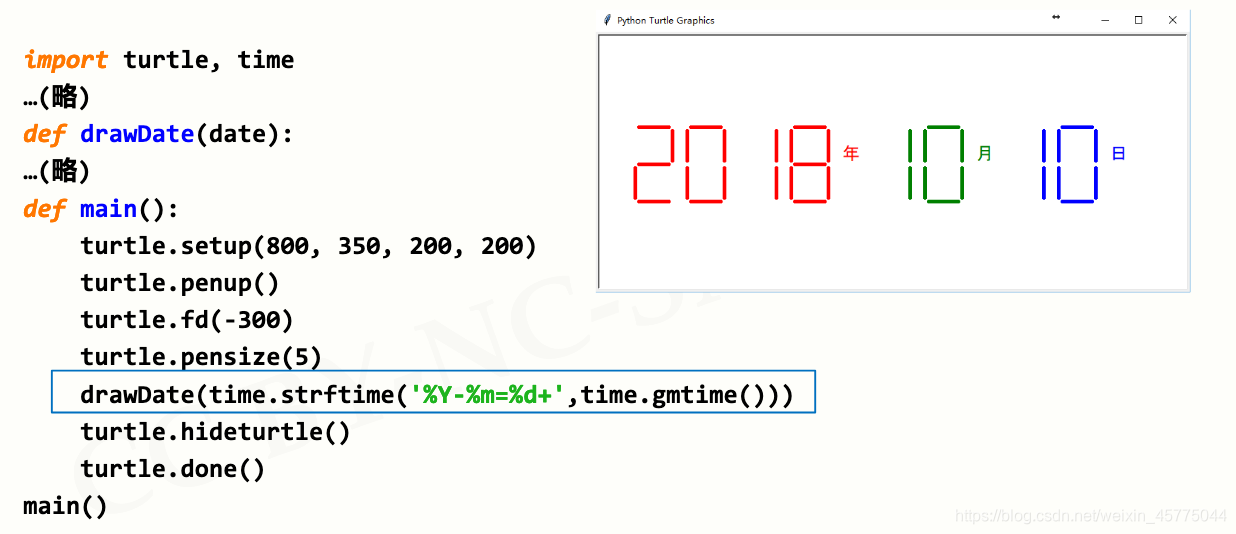
def main():turtle.setup(800, 350, 200, 200)turtle.penup()turtle.fd(-350)turtle.pensize(5)
# drawDate('2018-10=10+')drawDate(time.strftime('%Y-%m=%d+',time.gmtime()))turtle.hideturtle()turtle.done()
main()

5.2.3 实例讲解(下)
七段数码管绘制
基本思路
- 步骤1:绘制单个数字对应的数码管
- 步骤2:获得一串数字,绘制对应的数码管
- 步骤3:获得当前系统时间,绘制对应的数码管


步骤3: 获取系统时间,绘制七段数码管


5.3.4 举一反三
理解方法思维
- 模块化思维:确定模块接口,封装功能
- 规则化思维:抽象过程为规则,计算机自动执行
- 化繁为简:将大功能变为小功能组合,分而治之
应用问题的扩展
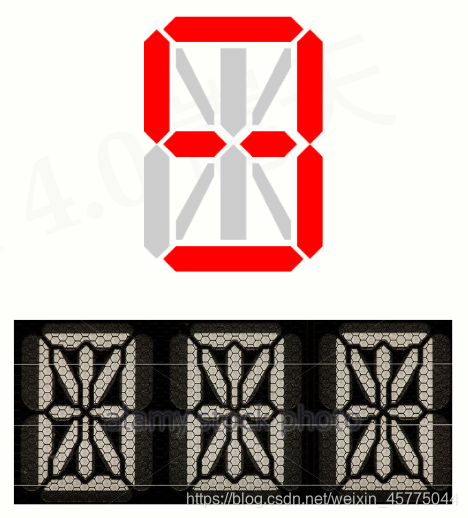
-绘制带小数点的七段数码管
-带刷新的时间倒计时效果
-绘制高级的数码管
- 5.3 代码复用与函数递归
目录:
- 代码复用与模块化设计
- 函数递归的理解
- 函数递归的调用过程
- 函数递归实例解析
小结:
-模块化设计:松耦合、紧耦合
-函数递归的2个特征:基例和链条
-函数递归的实现:函数+ 分支结构
5.3.1-代码复用与模块化设计
代码复用
把代码当成资源进行抽象
- 代码资源化:程序代码是一种用来表达计算的"资源"
- 代码抽象化:使用函数等方法对代码赋予更高级别的定义
- 代码复用:同一份代码在需要时可以被重复使用
函数和对象是代码复用的两种主要形式

模块化设计
分而治之
- 通过函数或对象封装将程序划分为模块及模块间的表达
- 具体包括:主程序、子程序和子程序间关系
- 分而治之:一种分而治之、分层抽象、体系化的设计思想
模块化设计
紧耦合 松耦合
- 紧耦合:两个部分之间交流很多,无法独立存在
- 松耦合:两个部分之间交流较少,可以独立存在
- 模块内部紧耦合、模块之间松耦合
5.3.2-函数递归的理解
如何理解递归呢?
递归很简单,无非就是一个函数调用自己而已…
-看过《盗梦空间》吗?本质上就是递归…
-学过数学归纳法吗?本质上就是递归…
-听过这个故事吗?本质上就是递归…
“从前有座山,山里有座庙,庙里有个老和尚在讲故事…”
递归的含义
函数定义中调用函数自身的方式

两个关键特征
- 链条:计算过程存在递归链条
- 基例:存在一个或多个不需要再次递归的基例
类似数学归纳法
- 数学归纳法
- 证明当n取第一个值n0时命题成立
- 假设当nk时命题成立,证明当n=nk+1时命题也成立
- 递归是数学归纳法思维的编程体现
5.3.3-函数递归的调用过程
递归的实现
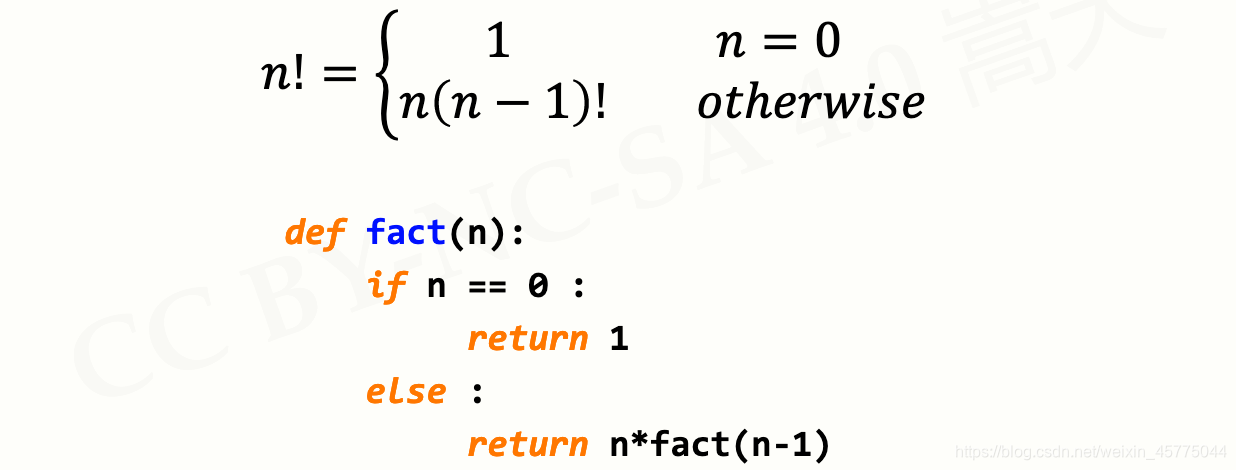
函数+ 分支语句
- 递归本身是一个函数,需要函数定义方式描述
- 函数内部,采用分支语句对输入参数进行判断
- 基例和链条,分别编写对应代码

5.3.4-函数递归实例解析
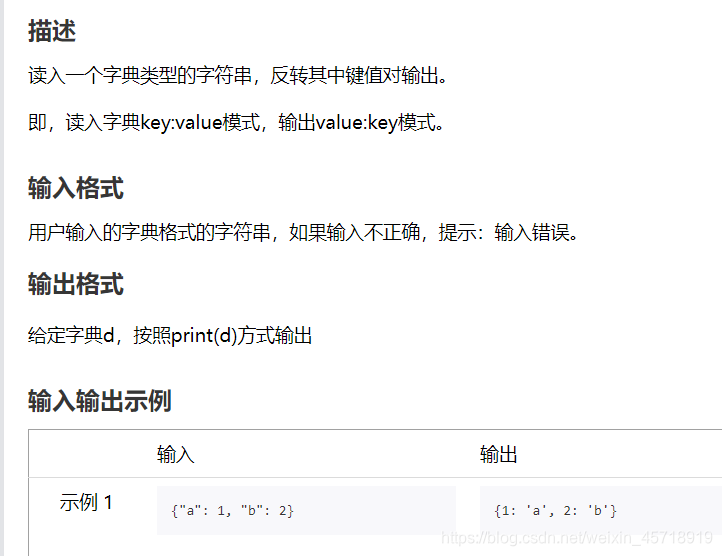
字符串反转
将字符串s反转后输出

斐波那契数列
一个经典数列
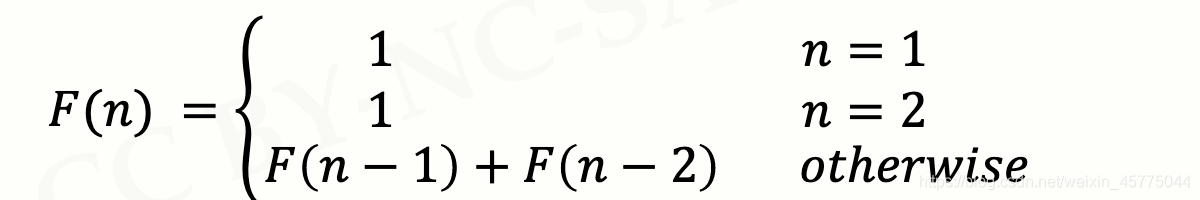

汉诺塔
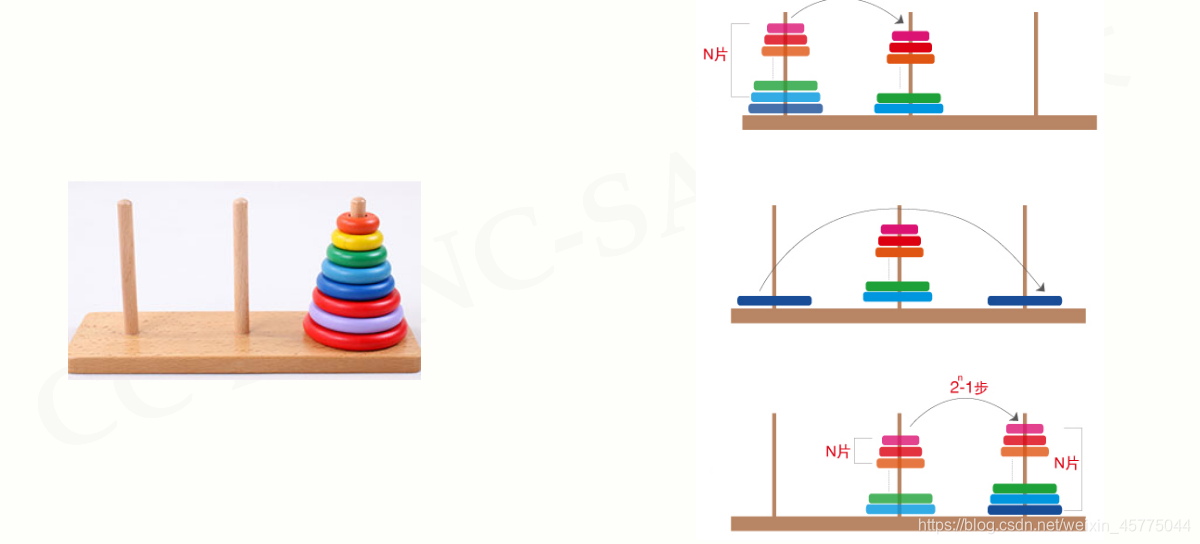
- 函数+ 分支结构
- 递归链条
- 递归基例
count = 0
def hanoi(n, src, dst, mid):global countif n == 1 :print("{}:{}->{}".format(1,src,dst))count+= 1else:hanoi(n- 1, src, mid, dst)print("{}:{}->{}".format(n,src,dst))count += 1hanoi(n- 1, mid, dst , src)
- 5.4模块4: PyInstaller库的使用
PyInstaller库基本介绍
PyInstaller库概述
将.py源代码转换成无需源代码的可执行文件
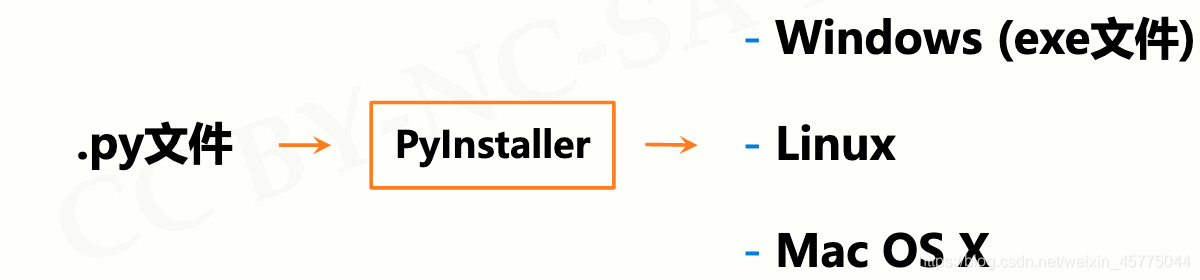
PyInstaller库是第三方库
- 官方网站:http://www.pyinstaller.org
- 第三方库:使用前需要额外安装
- 安装第三方库需要使用pip工具
(cmd命令行) pip install pyinstaller
PyInstaller库使用说明
简单的使用
(cmd命令行) pyinstaller-F <文件名.py>
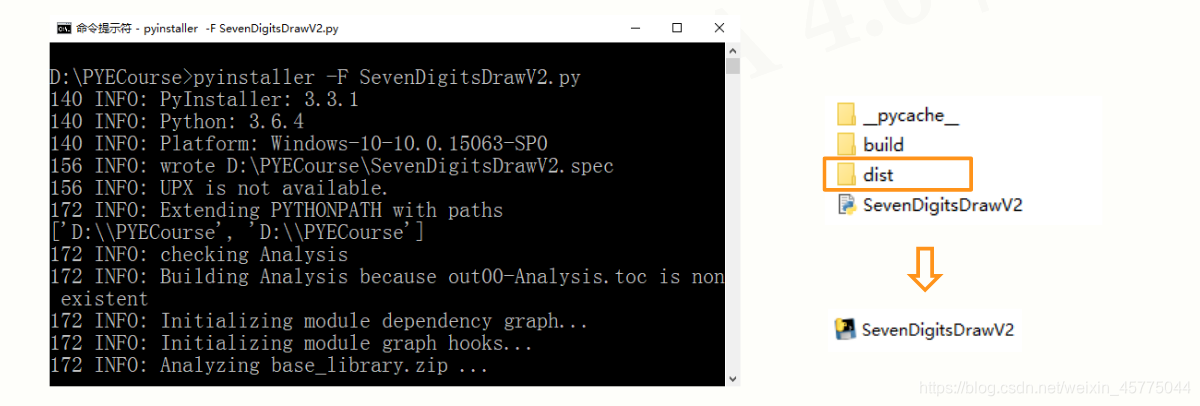
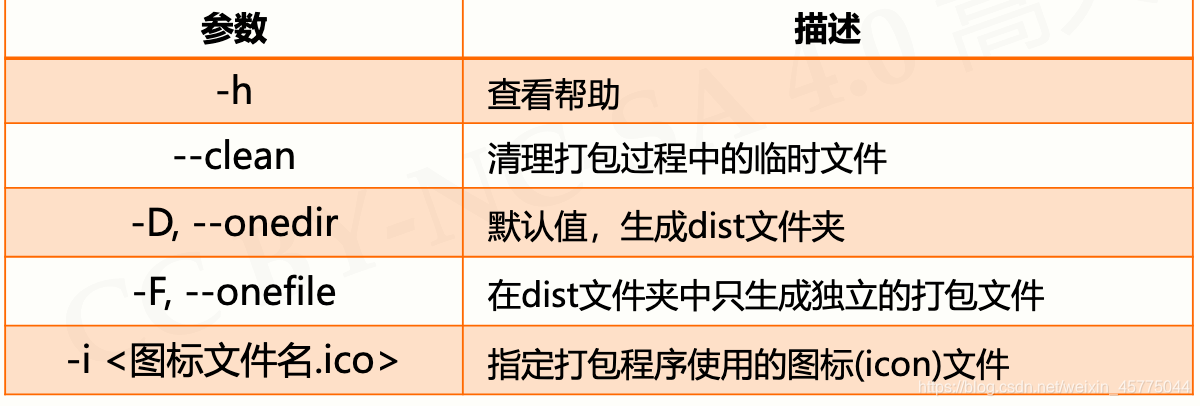
PyInstaller库常用参数
使用举例
pyinstaller–i curve.ico –F SevenDigitsDrawV2.py

- 5.5实例8: 科赫雪花小包裹
5.5.1 问题分析
科赫雪花
高大上的分形几何

-分形几何是一种迭代的几何图形,广泛存在于自然界中
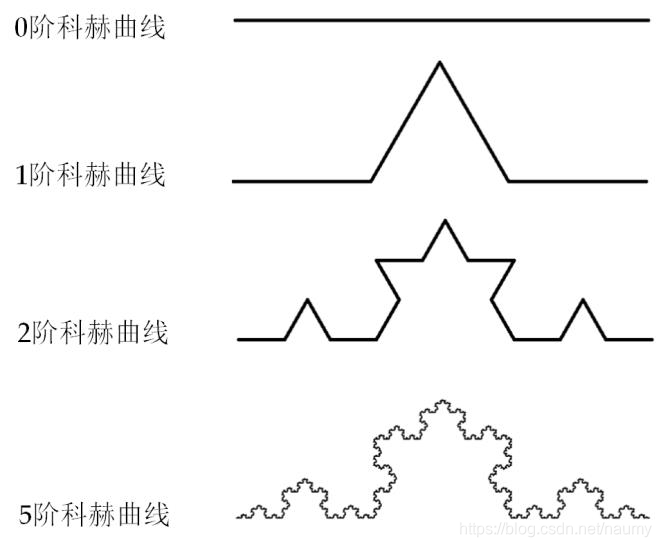
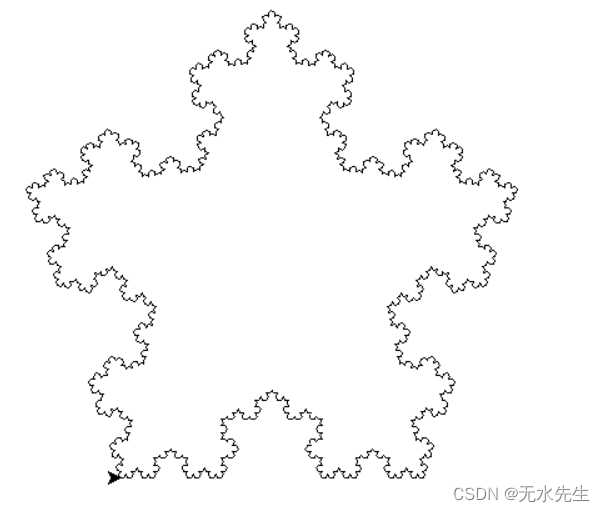
科赫曲线,也叫雪花曲线

科赫雪花绘制
用Python绘制科赫曲线
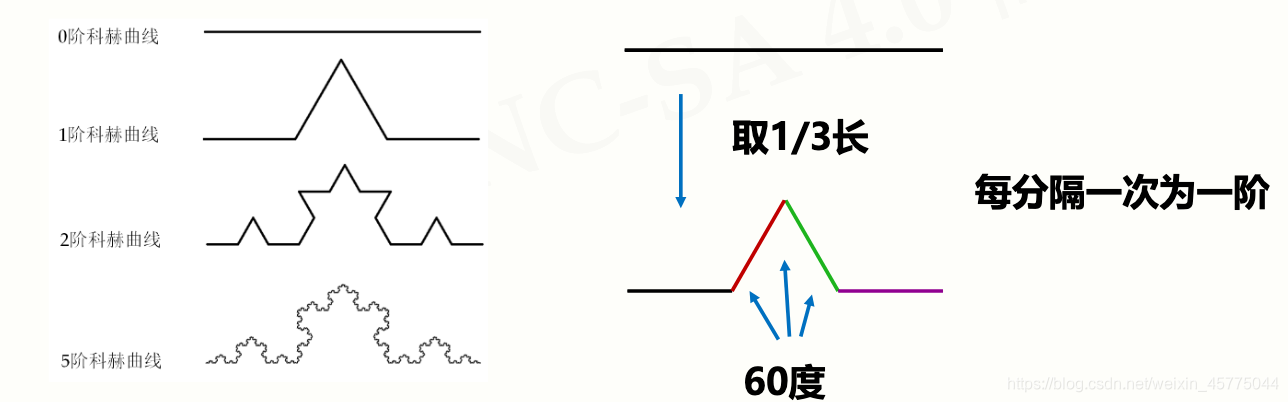
5.5.2 实例讲解(上)
科赫雪花小包裹(上)
科赫曲线的绘制
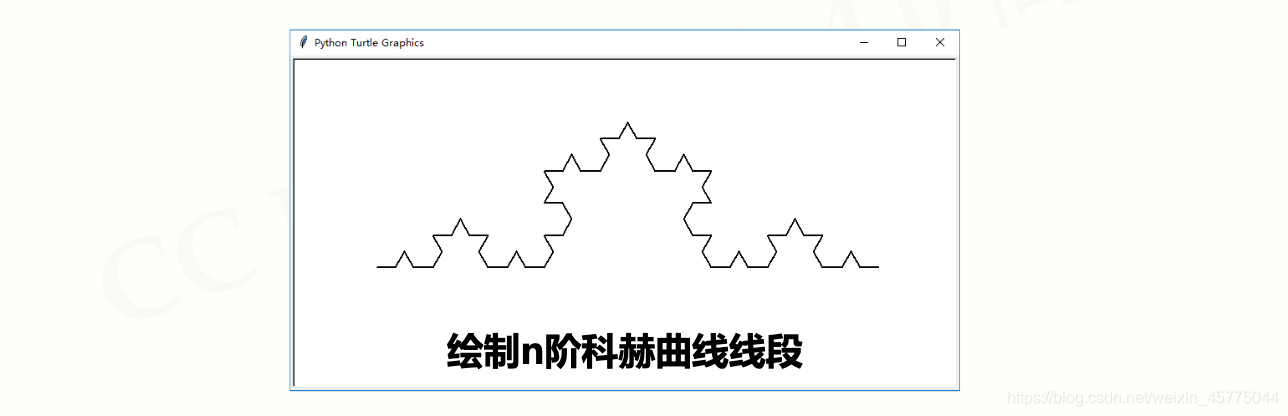
- 递归思想:函数+分支
- 递归链条:线段的组合
- 递归基例:初始线段
#KochDrawV1.py
import turtle
def koch(size, n):if n == 0:turtle.fd(size)else:for angle in [0, 60, -120, 60]:turtle.left(angle)koch(size/3, n-1)
def main():turtle.setup(800,400)turtle.penup()turtle.goto(-300, -50)turtle.pendown()turtle.pensize(2)koch(600,3) # 0阶科赫曲线长度,阶数turtle.hideturtle()
main()
科赫曲线的绘制➡️科赫雪花的绘制
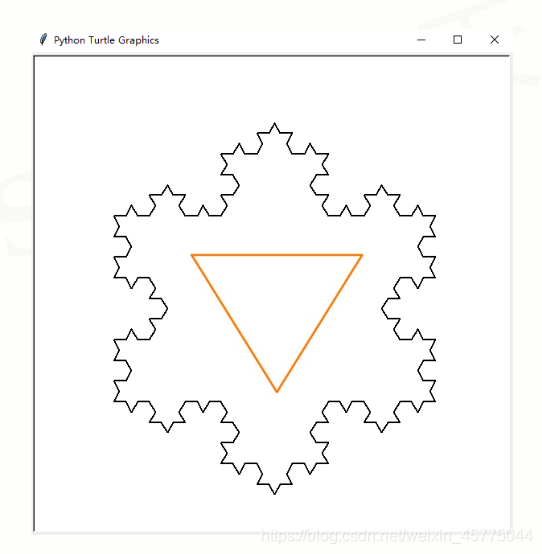
#KochDrawV2.py
import turtle
def koch(size, n):if n == 0:turtle.fd(size)else:for angle in [0, 60, -120, 60]:turtle.left(angle)koch(size/3, n-1)
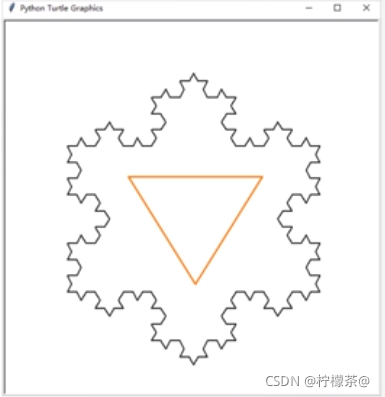
def main():turtle.setup(600,600)turtle.penup()turtle.goto(-200, 100)turtle.pendown()turtle.pensize(2)level = 3 # 3阶科赫雪花,阶数koch(400,level) turtle.right(120)koch(400,level)turtle.right(120)koch(400,level)turtle.hideturtle()
main()
5.5.3 实例讲解(下)
科赫雪花小包裹(下)
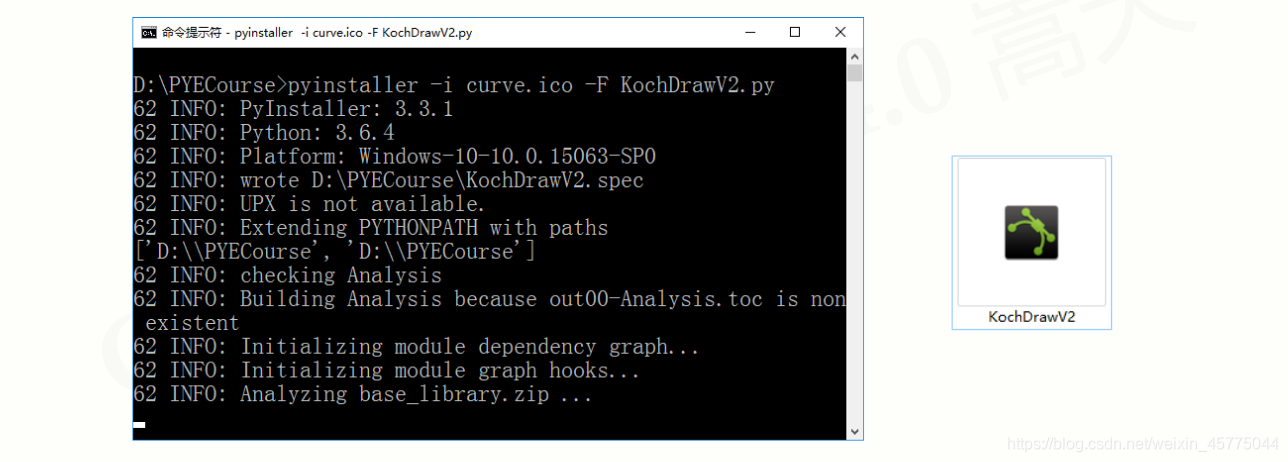
打包才能上路…
pyinstaller–i curve.ico –F KochDrawV2.py

-对编写后的科赫雪花代码进行打包处理
5.5.4 举一反三
绘制条件的扩展
- 修改分形几何绘制阶数
- 修改科赫曲线的基本定义及旋转角度
- 修改绘制科赫雪花的基础框架图形
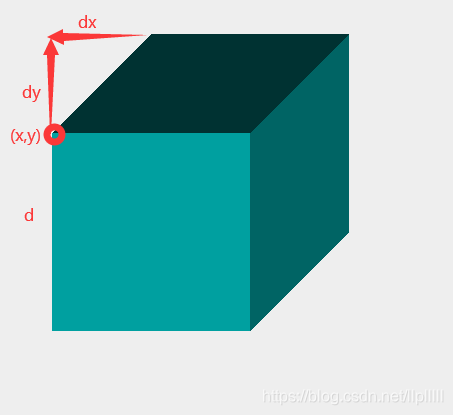
分形几何千千万
- 康托尔集、谢尔宾斯基三角形、门格海绵…
- 龙形曲线、空间填充曲线、科赫曲线…
- 函数递归的深入应用…