门格海绵的实现

article/2025/1/7 6:51:57

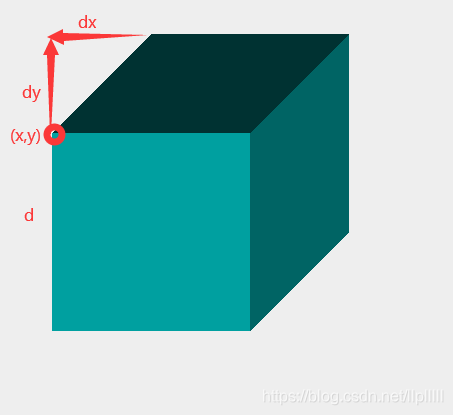
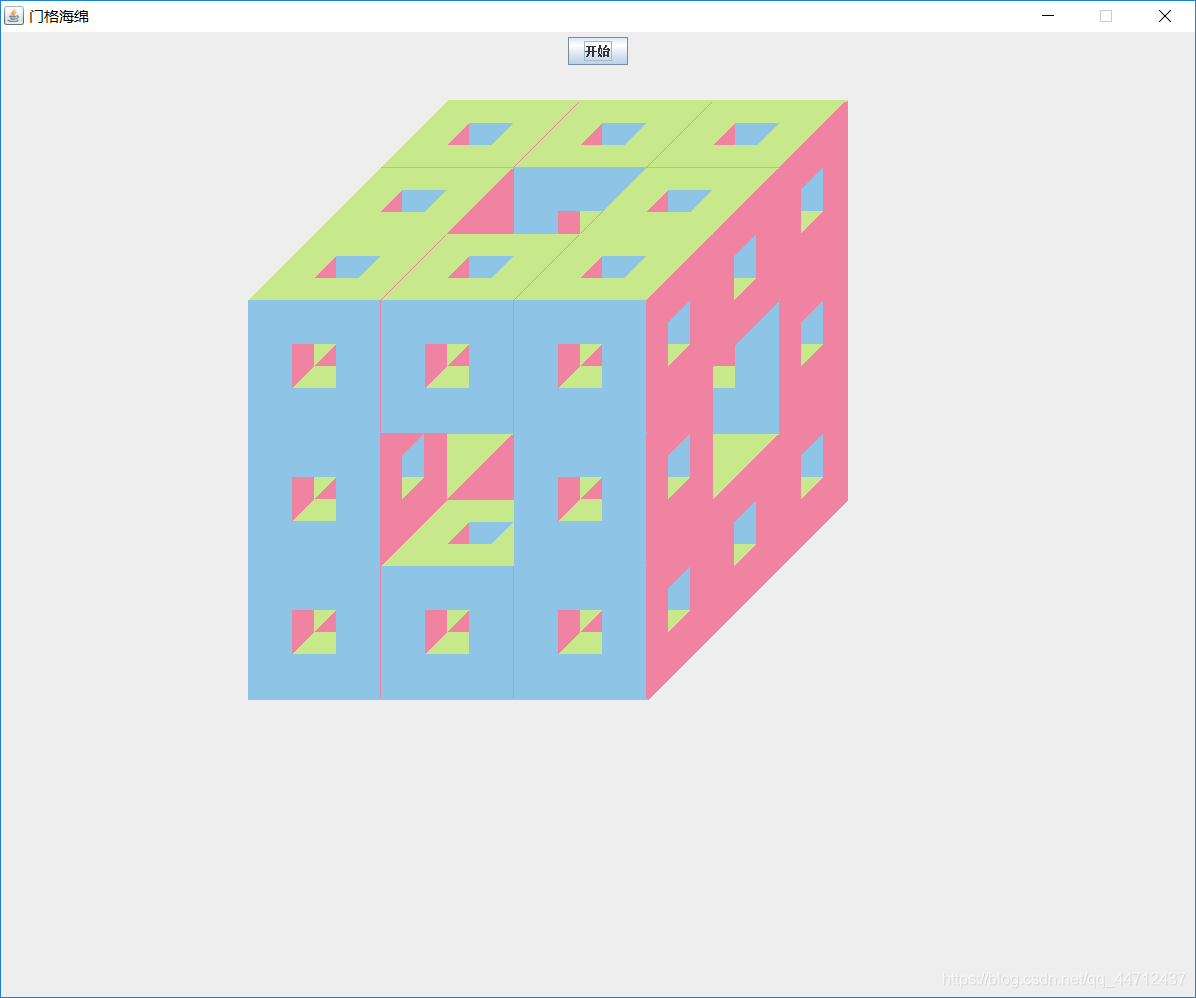
实现效果：
这里写图片描述
源代码：

package sponge;import java.awt.Color;
import java.awt.Graphics;
import java.awt.Graphics2D;
import java.awt.Point;
import java.awt.Polygon;import javax.swing.JFrame;public class Sponge_Main extends JFrame implements Runnable{public static void main(String[]  args) {Sponge_Main mf = new Sponge_Main();mf.initUI();}Point[] pn = new Point[20];public void paint(Graphics g) {super.paint(g);//正方形的顶点坐标int x = 100,y = 500;int d = 120,dx = 81,dy = 60;Point p0 = new Point(x,y);drawBottomLevel(g,p0,d,dx,dy);Point p1 = new Point(x,y-d);drawMidLevel(g,p1,d,dx,dy);Point p2 = new Point(x,y-2*d);drawTopLevel(g,p2,d,dx,dy);//----------for(int i = 0;i<pn.length;i++) {Point ptem = pn[i];if(ptem!=null) {Point ptem0 = new Point(pn[i].x,pn[i].y+2*d/3); drawBottomLevel(g,ptem0,d/3,dx/3,dy/3);Point ptem1 = new Point(pn[i].x,pn[i].y+d/3);drawMidLevel(g,ptem1,d/3,dx/3,dy/3);Point ptem2 = new Point(pn[i].x,pn[i].y);drawTopLevel(g,ptem2,d/3,dx/3,dy/3);}}}//根据起点p0得到另外6个点public Point[] getPointByP0(Point p0,int d,int dx,int dy) {Point p1 = new Point(p0.x+dx,p0.y-dy);Point p2 = new Point(p0.x+dx+d,p0.y-dy);Point p3 = new Point(p0.x+d,p0.y);Point p4 = new Point(p0.x+d,p0.y+d);Point p5 = new Point(p0.x,p0.y+d);Point p6 = new Point(p0.x+dx+d,p0.y+d-dy);Point[] ps = new Point[7];ps[0] = p0;ps[1] = p1;ps[2] = p2;ps[3] = p3;ps[4] = p4;ps[5] = p5;ps[6] = p6;return ps;}int count = 0;//递归次数public void draw(Graphics g,Point p0,Point p1,Point p2,Point p3,Point p4,Point p5,Point p6) {if(count<20) {pn[count] = p0;}count++;//三原色
//      int c1 = new java.util.Random().nextInt(255);
//      int c2 = new java.util.Random().nextInt(255);
//      int c3 = new java.util.Random().nextInt(255);Graphics2D gD = (Graphics2D) g;//填充面的颜色Polygon pon1 = new Polygon();//填充第一个可见面pon1.addPoint(p0.x, p0.y);pon1.addPoint(p1.x, p1.y);pon1.addPoint(p2.x, p2.y);pon1.addPoint(p3.x, p3.y);gD.setColor(new Color(230,0,0));gD.fillPolygon(pon1);//填充第二个可见面Polygon pon2 = new Polygon();pon2.addPoint(p0.x, p0.y);pon2.addPoint(p3.x, p3.y);pon2.addPoint(p4.x, p4.y);pon2.addPoint(p5.x, p5.y);gD.setColor(new Color(255,0,0));gD.fillPolygon(pon2);//填充第三个可见面Polygon pon3 = new Polygon();pon3.addPoint(p2.x, p2.y);pon3.addPoint(p3.x, p3.y);pon3.addPoint(p4.x, p4.y);pon3.addPoint(p6.x, p6.y);gD.setColor(new Color(200,0,0));gD.fillPolygon(pon3);}public void drawBottomLevel(Graphics g, Point p0, int d, int dx, int dy) {Point[] ps1 = getPointByP0(p0,d,dx,dy);Point[] ps2 = getPointByP0(ps1[3],d,dx,dy);Point[] ps3 = getPointByP0(ps2[3],d,dx,dy);Point[] ps4 = getPointByP0(ps3[1],d,dx,dy);Point[] ps5 = getPointByP0(ps4[1],d,dx,dy);Point[] ps6 = getPointByP0(ps1[1],d,dx,dy);Point[] ps7 = getPointByP0(ps6[1],d,dx,dy);Point[] ps8 = getPointByP0(ps7[3],d,dx,dy);draw(g,ps7[0],ps7[1],ps7[2],ps7[3],ps7[4],ps7[5],ps7[6]);try {Thread.sleep(100);} catch (InterruptedException e) {// TODO Auto-generated catch blocke.printStackTrace();}draw(g,ps8[0],ps8[1],ps8[2],ps8[3],ps8[4],ps8[5],ps8[6]);try {Thread.sleep(100);} catch (InterruptedException e) {// TODO Auto-generated catch blocke.printStackTrace();}draw(g,ps5[0],ps5[1],ps5[2],ps5[3],ps5[4],ps5[5],ps5[6]);try {Thread.sleep(100);} catch (InterruptedException e) {// TODO Auto-generated catch blocke.printStackTrace();}draw(g,ps4[0],ps4[1],ps4[2],ps4[3],ps4[4],ps4[5],ps4[6]);try {Thread.sleep(100);} catch (InterruptedException e) {// TODO Auto-generated catch blocke.printStackTrace();}draw(g,ps6[0],ps6[1],ps6[2],ps6[3],ps6[4],ps6[5],ps6[6]);try {Thread.sleep(100);} catch (InterruptedException e) {// TODO Auto-generated catch blocke.printStackTrace();}draw(g,ps1[0],ps1[1],ps1[2],ps1[3],ps1[4],ps1[5],ps1[6]);try {Thread.sleep(100);} catch (InterruptedException e) {// TODO Auto-generated catch blocke.printStackTrace();}draw(g,ps2[0],ps2[1],ps2[2],ps2[3],ps2[4],ps2[5],ps2[6]);try {Thread.sleep(100);} catch (InterruptedException e) {// TODO Auto-generated catch blocke.printStackTrace();}draw(g,ps3[0],ps3[1],ps3[2],ps3[3],ps3[4],ps3[5],ps3[6]);try {Thread.sleep(100);} catch (InterruptedException e) {// TODO Auto-generated catch blocke.printStackTrace();}}public void drawMidLevel(Graphics g, Point p0, int d, int dx, int dy) {Point[] ps1 = getPointByP0(p0,d,dx,dy);Point[] ps2 = getPointByP0(ps1[3],d,dx,dy);Point[] ps3 = getPointByP0(ps2[3],d,dx,dy);Point[] ps4 = getPointByP0(ps3[1],d,dx,dy);Point[] ps5 = getPointByP0(ps4[1],d,dx,dy);Point[] ps6 = getPointByP0(ps1[1],d,dx,dy);Point[] ps7 = getPointByP0(ps6[1],d,dx,dy);Point[] ps8 = getPointByP0(ps7[3],d,dx,dy);draw(g,ps7[0],ps7[1],ps7[2],ps7[3],ps7[4],ps7[5],ps7[6]);draw(g,ps5[0],ps5[1],ps5[2],ps5[3],ps5[4],ps5[5],ps5[6]);draw(g,ps1[0],ps1[1],ps1[2],ps1[3],ps1[4],ps1[5],ps1[6]);draw(g,ps3[0],ps3[1],ps3[2],ps3[3],ps3[4],ps3[5],ps3[6]);}public void drawTopLevel(Graphics g, Point p0, int d, int dx, int dy) {Point[] ps1 = getPointByP0(p0,d,dx,dy);Point[] ps2 = getPointByP0(ps1[3],d,dx,dy);Point[] ps3 = getPointByP0(ps2[3],d,dx,dy);Point[] ps4 = getPointByP0(ps3[1],d,dx,dy);Point[] ps5 = getPointByP0(ps4[1],d,dx,dy);Point[] ps6 = getPointByP0(ps1[1],d,dx,dy);Point[] ps7 = getPointByP0(ps6[1],d,dx,dy);Point[] ps8 = getPointByP0(ps7[3],d,dx,dy);draw(g,ps7[0],ps7[1],ps7[2],ps7[3],ps7[4],ps7[5],ps7[6]);draw(g,ps8[0],ps8[1],ps8[2],ps8[3],ps8[4],ps8[5],ps8[6]);draw(g,ps5[0],ps5[1],ps5[2],ps5[3],ps5[4],ps5[5],ps5[6]);draw(g,ps4[0],ps4[1],ps4[2],ps4[3],ps4[4],ps4[5],ps4[6]);draw(g,ps6[0],ps6[1],ps6[2],ps6[3],ps6[4],ps6[5],ps6[6]);draw(g,ps1[0],ps1[1],ps1[2],ps1[3],ps1[4],ps1[5],ps1[6]);draw(g,ps2[0],ps2[1],ps2[2],ps2[3],ps2[4],ps2[5],ps2[6]);draw(g,ps3[0],ps3[1],ps3[2],ps3[3],ps3[4],ps3[5],ps3[6]);}public void initUI() {this.setTitle("门格海绵");this.setSize(1000, 800);this.setDefaultCloseOperation(3);this.setResizable(false);this.setLocationRelativeTo(null);this.setVisible(true);}@Overridepublic void run() {// TODO Auto-generated method stub}
}

http://chatgpt.dhexx.cn/article/4jUgQujt.shtml

相关文章

混沌与分形（一）：谢尔宾斯基三角形与门格海绵

混沌与分形（一）：谢尔宾斯基三角形与门格海绵

研究混沌运动&#xff0c;少不了对分形理论的探讨。分形&#xff1a;通常被定义为“一个粗糙或零碎的几何形状&#xff0c;可以分成数个部分&#xff0c;且每一部分都&#xff08;至少近似地&#xff09;是整体缩小后的形状”&#xff0c;即具有自相似的性质。 本篇将从一维过…
阅读更多...
分形之门格海绵

分形之门格海绵

门格海绵解决思路&#xff1a; 1. 迭代如何实现 2. 立方体该怎么画 3. 实现门格海绵代码 4. 画图板门格海绵代码 1. 迭代如何实现 为了实现从1图—>2图—>3图效果,我们就要想到用迭代去实现. 因为像3图这样的图形,是由若干个2图这样的基本图形组成的 那么,怎样实现…
阅读更多...
JAVA学习日志之门格海绵

JAVA学习日志之门格海绵

门格海绵的结构可以用以下方法形象化&#xff1a; 从一个正方体开始。&#xff08;第一个图像&#xff09; 把正方体的每一个面分成9个正方形。这将把正方体分成27个小正方体&#xff0c;像魔方一样。 把每一面的中间的正方体去掉&#xff0c;把最中心的正方体也去掉&#xff0…
阅读更多...
复杂分形，简单规则：门格海绵世界探秘

复杂分形，简单规则：门格海绵世界探秘

连绵的山川、飘浮的云朵、岩石的断裂口、布朗粒子运动的轨迹、树冠、花菜、大脑皮层……这些部分与整体以某种方式相似的形体&#xff0c;可以说&#xff0c;就是“分形”的要义了&#xff0c;也恰恰是这些“不规则的”、“分散的”、“支离破碎的”物体又重新让我们认识了自然…
阅读更多...
JQData | 高校版使用教程，30秒安装完成，自带Python环境

JQData | 高校版使用教程，30秒安装完成，自带Python环境

本地量化金融数据JQData&#xff0c;是聚宽数据团队专门为金融机构、学术团体和量化研究者们提供的本地量化金融数据服务。自有版权&#xff0c;支持国内多家头部券商实盘交易。历经15万量化研究者与数百家机构使用验证。 JQData目前已支持国内30 高校&#xff0c;本次更新&…
阅读更多...
JQData + matplotlib 实现回测日志的交易细节可视化 量化数据接口

JQData + matplotlib 实现回测日志的交易细节可视化 量化数据接口

原文&#xff1a;https://zhuanlan.zhihu.com/p/49051899 前言&#xff1a; 做量化交易的朋友都知道回测的重要性&#xff0c;回测结果是衡量一个量化交易策略是否靠谱的重要依据。回测平台会按历史行情数据模拟成交&#xff0c;并将回测结果汇总成报告。 在很多时候&#xf…
阅读更多...
Note: Python学习笔记 -- Anaconda install jqdata

Note: Python学习笔记 -- Anaconda install jqdata

运行代码下列代码&#xff0c;提示错误 没有安装 jqdata。打开Anaconda Prompt 输入 pip install jqdata 提示cannot find command git然后百度了半天&#xff0c;有人说 pip install git 出错可以使用 conda install git 但是依然出错。最后去官网下载了Git:https://git-scm.…
阅读更多...
jq使用教程01_最贴心教程，安装JQData全靠这篇指南

jq使用教程01_最贴心教程，安装JQData全靠这篇指南

Hi, 各位亲爱的小伙伴们&#xff01; 近来听说有部分小伙伴在安装JQData时遇到了点小麻烦&#xff0c;导致最后没有安装成功&#xff0c;为了帮助小伙伴们快速成功安装JQData&#xff0c;小编今天来为大家排一下“雷”&#xff0c;希望能帮到你们哟 (&#xff65;ω&#xff6…
阅读更多...
事件驱动的选股小工具（JQData）

事件驱动的选股小工具（JQData）

昨天发改委下发了《关于积极推进风电、光伏发电无补贴平价上网有关工作的通知》&#xff0c;也不知道对股市是利空还是利多。连夜做了一个搜索公司经营范围的小工具,看看那些股票受到影响。 以后还可以增加筛选条件&#xff0c;比如财务指标&#xff0c;剔除ST股票&#xff0c;…
阅读更多...
股票python量化交易008-JoinQuant中JQData的使用

股票python量化交易008-JoinQuant中JQData的使用

查阅JoinQuant中JQData的使用文档python代码实现导入JQData，并认证用户身份。认证完毕显示“auth success”后即可使用 from jqdatasdk import *; auth(ID,Password);#ID是申请时所填写的手机号；Password为聚宽官网登录密码 # 查询jqdata的调用次数情况 surplus_count = g…
阅读更多...
jqdata pyechart： 用grid双图实现k线带图成交 — by QUANTAXIS

jqdata pyechart： 用grid双图实现k线带图成交 — by QUANTAXIS

from jqdatasdk import * from pyecharts import Kline,Bar,Grid 首先我们先应JQDATA 的活动演示一下如何调用pyecharts 画图 auth(acc,password) dataget_price(000001.XSHE) auth success先打印下 data 我们可以看到 jqdata返回的格式是 一个单index的Dataframe data.he…
阅读更多...
Quant | JQData使用API简单梳理（二）

Quant | JQData使用API简单梳理（二）

聚宽平台实际上提供了两种查询数据的方法，第一种是线上在聚宽平台可以使用的API：jqdata，另外一种则是本地的接口：JQData，是的，你没有看错，只是大小写的不同，搞得一开始我以为完全是同一种。jqdata可以线上通过import jqdata来引入数据接口，本地的JQData则是通过import…
阅读更多...
jqdata(data是什么文件格式)

jqdata(data是什么文件格式)

期货交易中bar和tick是什么意思 Bar 的概念 在一定时间段内的时间序列就构成了一根 K 线(日本蜡烛图)&#xff0c;单根 K 线被称为 Bar。 如果是一分钟内的 Tick 序列&#xff0c;即构成一根分钟 K 线&#xff0c;又称分钟 Bar; 如果是一天内的分钟序列&#xff0c;即构成一根日…
阅读更多...
JQData | 量化界最好用的本地量化金融数据（free free~）

JQData | 量化界最好用的本地量化金融数据（free free~）

什么是本地量化金融数据 - JQData &#xff1f; 使用JQData本地量化金融数据服务&#xff0c;可快速查看、计算或接入金融数据信息&#xff0c;解决本地、web、自研金融终端调用数据的需求。支持python多版本及多操作系统。为财经类企业、金融机构、学术研究机构和量化爱好者们…
阅读更多...
获取股票数据【使用JQData查询行情数据、财务指标、估值指标】

获取股票数据【使用JQData查询行情数据、财务指标、估值指标】

了解股票&#xff1a; 在上一次量化小科普【什么是量化&#xff1f;常用的股票量化指标、如何搭建量化交易系统】对于量化的概念有了一个基本认识&#xff0c;其中量化的主体在这门课程的学习中是“股票”&#xff0c;而当别人问你&#xff1a;“什么是股票&#xff1f;”&…
阅读更多...
JQData安装的问题（本地调用的量化金融数据接口-免费）

JQData安装的问题（本地调用的量化金融数据接口-免费）

JQData简介（1）JQData是聚宽数据团队专门为有志于从事量化投资的金融机构、研究人员以及个人量化爱好者提供的本地量化金融数据。用户只需在本地Python环境下安装JQData数据包，输入三行代码，即可调用由聚宽数据团队专业生产的全套量化金融数据，让你轻松告别平台限制，灵活安…
阅读更多...
JQData安装(转)

JQData安装(转)

首先&#xff0c;JQData是基于python的一个数据包&#xff0c;所以安装JQData的第一步是安装Python &#xff08;没有接触过python或者python基础不好的小伙伴&#xff0c;可以关注聚宽量化课堂的python讲堂进行python学习&#xff09;。 对于python安装包的选择&#xff0c;…
阅读更多...
JQData安装的问题（只解决安装的问题）

JQData安装的问题（只解决安装的问题）

1. JQData简介 &#xff08;1&#xff09;JQData是聚宽数据团队专门为有志于从事量化投资的金融机构、研究人员以及个人量化爱好者提供的本地量化金融数据。用户只需在本地Python环境下安装JQData数据包&#xff0c;输入三行代码&#xff0c;即可调用由聚宽数据团队专业生产的…
阅读更多...
JQData-本地调用的量化金融数据接口（免费）

JQData-本地调用的量化金融数据接口（免费）

什么是聚宽数据-JQData？ 使用JQData金融数据服务，可快速查看、计算或接入金融数据信息，解决本地、web、自研金融终端调用数据的需求。支持python多版本及多操作系统。为财经类企业、金融机构、学术研究机构和量化爱好者们提供一站式财经信息服务及数据解决方案。 提供哪些…
阅读更多...
JQData安装 | 最贴心教程，安装JQData全靠这篇指南

JQData安装 | 最贴心教程，安装JQData全靠这篇指南

转自 JQData安装 | 最贴心教程&#xff0c;安装JQData全靠这篇指南 Hi, 各位亲爱的小伙伴们&#xff01; 首先&#xff0c;感谢聚宽小编 JQData01 给我开放了更多的数据访问资源 近来听说有部分小伙伴在安装JQData时遇到了点小麻烦&#xff0c;导致最后没有安装成功&#xff0c…
阅读更多...
推荐文章

Copyright @ 2022~2023