Java第六课——画图板

article/2025/1/6 19:48:26

Java第六课——画图板

这节课画一个画图板，可以画线画圆，还可以通过递归画出好看的图案如：谢尔宾斯基三角形，康托尔方形集，甚至立体图门格海绵。

首先创建一个窗体。定义一个类和一个方法。

public class Draw{public void show(){JFrame frame =new JFrame();FlowLayout layout=new FlowLayout();frame.setLayout(layout);frame.setSize(1000,1000);frame.setVisible(true);}public static void main(String[] args){Draw ui=new Draw();ui.show();}
}

再添加监听器
这里的监听器就不只是ActionListener了，由于是画图板，不仅要有按钮来判断是花园画圆还是划线，这里要用到动作监听器；而且要获取鼠标的位置来划线，要用到鼠标监听器MouseListener或者MouseMotionListener，这两者的区别如下:
MouseListener的鼠标事件有:
MOUSE_CLICKED 鼠标点击(要求比较苛刻，按下和松开必须是同一个像素格)
MOUSE_ENTERED 鼠标进入(某个窗体)
MOUSE_EXITED 鼠标离开
MOUSE_PRESSED 鼠标按下
MOUSE_RELEASED 鼠标松开
MouseMotionListener的鼠标事件有:
MOUSE_DRAGGED 鼠标拖拽
MOUSE_MOVED 鼠标移动
那么在划线时，推荐使用MouseListener里的mousePressed和mouseReleased。因为在拖拽时会持续划线，导致线越来越粗。
1、添加监听器，要额外创建一个类DrawListener
2、划线需要一支画笔，要用到Graphics，需要在监听器类和画图板类中都实例化一个Graphics的对象，并且让二者相等。
3、在这个类中还需要划线起始点和终止点的坐标值startx,starty,endx,endy。获取坐标的方法就由getX()和getY()来实现。
4、创建并添加监听器后，每次按下按钮，系统需要获取最近一次按下按钮的名称，根据该名称来判断应该是划线还是画圆，就需要一个空的String用于存储。

public class DrawListener implements MouseListener,ActionListener{//坐标int startx,starty,endx,endy;//GraphicsGraphics g;//存储上一次按钮的名称String str="";//补齐函数public void actionPerformed(ActionEvent a){}public void mousePressed(MouseEvent e){}public void mouseReleased(MouseEvent e){}public void mouseClicked(MouseEvent e) {}public void mouseEntered(MouseEvent e) {}public void mouseExited(MouseEvent e) {}
}

在Draw类show方法中
1、Graphics获取的画笔必须在设置可视之后
2、为窗体添加按钮，并且为按钮添加ActionListener，当按钮数量比较多时，可以用数组(下一课会详细介绍，先按模板来)

public class Draw{public void show(){JFrame frame =new JFrame();FlowLayout layout=new FlowLayout();frame.setLayout(layout);frame.setSize(1000,1000);DrawListener lis=new DrawListener();frame.addMouseListener(lis);//利用数组添加按钮String[] name={"直线","圆形","谢尔宾斯基三角形","康托尔方形集","门格海绵"}//通过for循环生成按钮并添加监听器for(int i=0;i<name.length;i++){JButton btn=new JButton(name[i]);frame.add(btn);btn.addActionListener(lis);}frame.setVisible(true);//从frame中获取位置，传回监听器类Graphics g=frame.getGraphics();lis.g=g;}public static void main(String[] args){Draw ui=new Draw();ui.show();}
}

可以通过Dimension来调节按钮大小，让界面更美观，在界面那节课讲到，这里不多赘述。
接下来的任务是先获取按钮文本，在actionPerformed(ActionEvent a)中，用a.getActionCommand()得到按钮文本放到str中

public void actionPerformed(ActionEvent a){str=a.getActionCommand();
}

在pressed和released中获取startx，starty，endx，endy的值

public void mousePressed(MouseEvent e){startx = e.getX();starty = e.getY();
}
public void mouseReleased(MouseEvent e){endx = e.getX();endY = e.getY();
}

划线,画圆

划线是一个过程，也就是先按下鼠标，拖动，再松开鼠标，那么就上当鼠标松开时划线。划线用drawLine(int x1,int y1,int x2,int y2)
画圆也是同理，用drawOval(int x1,int y1,int width,int height)，这里可能存在startx>endx,starty>endy的情况，那么加入数学函数Math.min(startx,endx)即可,宽度用endx-startx的绝对值Math.abs(endx-startx)

public void mouseReleased(MouseEvent e){endx = e.getX();endY = e.getY();if("直线".equals(str)){g.drawLine(startx,starty,endx,endy);}if("圆形".equals(str)){g.drawOval(Math.min(endx, startx), Math.min(starty, endy), Math.abs(endx-startx), Math.abs(endy-starty));}
}

谢尔宾斯基三角形

谢尔宾斯基三角形可以看出每个白色三角形内部都会分出三个白色三角形和一个黑色三角形，所以利用递归能很轻松的画出谢尔宾斯基三角形，只需要每次都找到白色三角形各边的中点，连接起来并涂黑就可以完成，涂黑用fillPolygon(int [ ] xPoints,int [ ] yPoints,int nPoints)前面两个数组为x,y坐标的数组，最后的nPoints表示所填充的多边形顶点个数
创建一个新的类,并利用函数triangle画出三角形

public class Sierpinskitriangle{public void triangle(){}
}

设n为找中点的次数，设(x1,y1)(x2,y2)(x3,y3)为最大三角形三个顶点的坐标
那么首先先把最开始的三个点之间连起来，并且获取各个中点代入数组:

g.drawLine(x1, y1, x2, y2);
g.drawLine(x1, y1, x3, y3);
g.drawLine(x2, y2, x3, y3);
int[] x={(x1+x2)/2,(x1+x3)/2,(x2+x3)/2};
int[] y={(y1+y2)/2,(y1+y3)/2,(y3+y2)/2};

当n=1时，涂黑 fillPolygon(x, y, 3)
当n增加时，要调用自己三次使得新的三个白色三角形都能再分出新的三角形，那么只需把x1,y1,x2,y2,x3,y3赋予新的三角形的三个顶点即可，所以通过形参直接赋值会方便的多，于是可以用到下面的函数头public void triangle(Graphics g,int n,int x1,int x2,int x3,int y1,int y2,int y3),Graphics g可以直接通过形参拿到画笔
那么当n=2时,三个triangle(g,2-1,x1,x2,x3,y1,y2,y3)，这里的三个顶点为三个白色三角形的顶点，然后每次调用后都接fillPolygon(x, y, 3)
n=3时,三个triangle(g,3-1,x1,x2,x3,y1,y2,y3),fillPolygon(x, y, 3)
每次调用自己时都要涂黑显得麻烦，不如使得n=1时什么都不做，让涂黑到主程序里:

public class Sierpinskitriangle{public void triangle(Graphics g,int n,int x1,int x2,int x3,int y1,int y2,int y3){int[] x={(x1+x2)/2,(x1+x3)/2,(x2+x3)/2};int[] y={(y1+y2)/2,(y1+y3)/2,(y3+y2)/2};g.drawLine(x1, y1, x2, y2);g.drawLine(x1, y1, x3, y3);g.drawLine(x2, y2, x3, y3);g.fillPolygon(x, y, 3);if(n==1){return;}triangle(g,n-1,x1,(x1+x2)/2,(x1+x3)/2,y1,(y1+y2)/2,(y1+y3)/2);triangle(g,n-1,x2,(x1+x2)/2,(x2+x3)/2,y2,(y1+y2)/2,(y2+y3)/2);triangle(g,n-1,x3,(x1+x3)/2,(x2+x3)/2,y3,(y1+y3)/2,(y2+y3)/2);}
}

那么在监听器类中可在mouseReleased(MouseEvent e)函数中，像直线和画圆一样，if(“谢尔宾斯基三角形”.equals(str))，则创建一个对象并调用方法

if("谢尔宾斯基三角形".equals(str)){Sierpinskitriangle triangle=new Sierpinskitriangle();triangle.triangle(g,5,500,100,900,100,900,900);

当n=5时画出的图像和上图一样

康托尔方形集康托尔方形集

先创建一个类和一个方法

public class CantorSquareset{public void csset(){}
}

用drawRect(int x1,int y1,int width,int height)画矩形
给n下个定义，最开始有一个最大的矩形。当n=1时，画出中间的第二大的矩形；n=2时，画出第二大矩形周围8个第三大的矩形。那么从1开始n每加一，就需要调用8次函数本身，而其实只需要找到这八次的八个矩形的顶点，那么利用函数头csset(Graphics g,int n,int x1,int y1,int x2,int y2) 其中(x1,y1)(x1,y2)分别时矩形的左上角和右下角
那么当n=1时，中间矩形 drawRect(x1+(x2-x1)/3, y1+(y2-y1)/3, (x2-x1)/3, (y2-y1)/3)
当n=2时，找出各小矩形左上角和长宽

public class CantorSquareset{public void csset(Graphics g,int n,int x1,int y1,int x2,int y2){g.drawRect(100, 100, 800, 800);if(n==1){ g.drawRect(x1+(x2-x1)/3, y1+(y2-y1)/3, (x2-x1)/3, (y2-y1)/3);return;}csset(g,n-1,x1,y1,x2,y2);csset(g,n-1,x1,y1,x1+(x2-x1)/3,y1+(y2-y1)/3);csset(g,n-1,x1+(x2-x1)/3,y1,x2-(x2-x1)/3,y1+(y2-y1)/3);csset(g,n-1,x2-(x2-x1)/3,y1,x2,y1+(y2-y1)/3);csset(g,n-1,x1,y1+(y2-y1)/3,x1+(x2-x1)/3,y2-(y2-y1)/3);csset(g,n-1,x2-(x2-x1)/3,y1+(y2-y1)/3,x2,y2-(y2-y1)/3);csset(g,n-1,x1,y2-(y2-y1)/3,x1+(x2-x1)/3,y2);csset(g,n-1,x1+(x2-x1)/3,y2-(y2-y1)/3,x2-(x2-x1)/3,y2);csset(g,n-1,x2-(x2-x1)/3,y2-(y2-y1)/3,x2,y2);}
}

在mouseReleased(MouseEvent e)函数中

if("康托尔方形集".equals(str)){CantorSquareset csset=new CantorSquareset();csset.csset(g, 3, 100, 100, 900, 900);}

当n=3时图案和上图一样

门格海绵

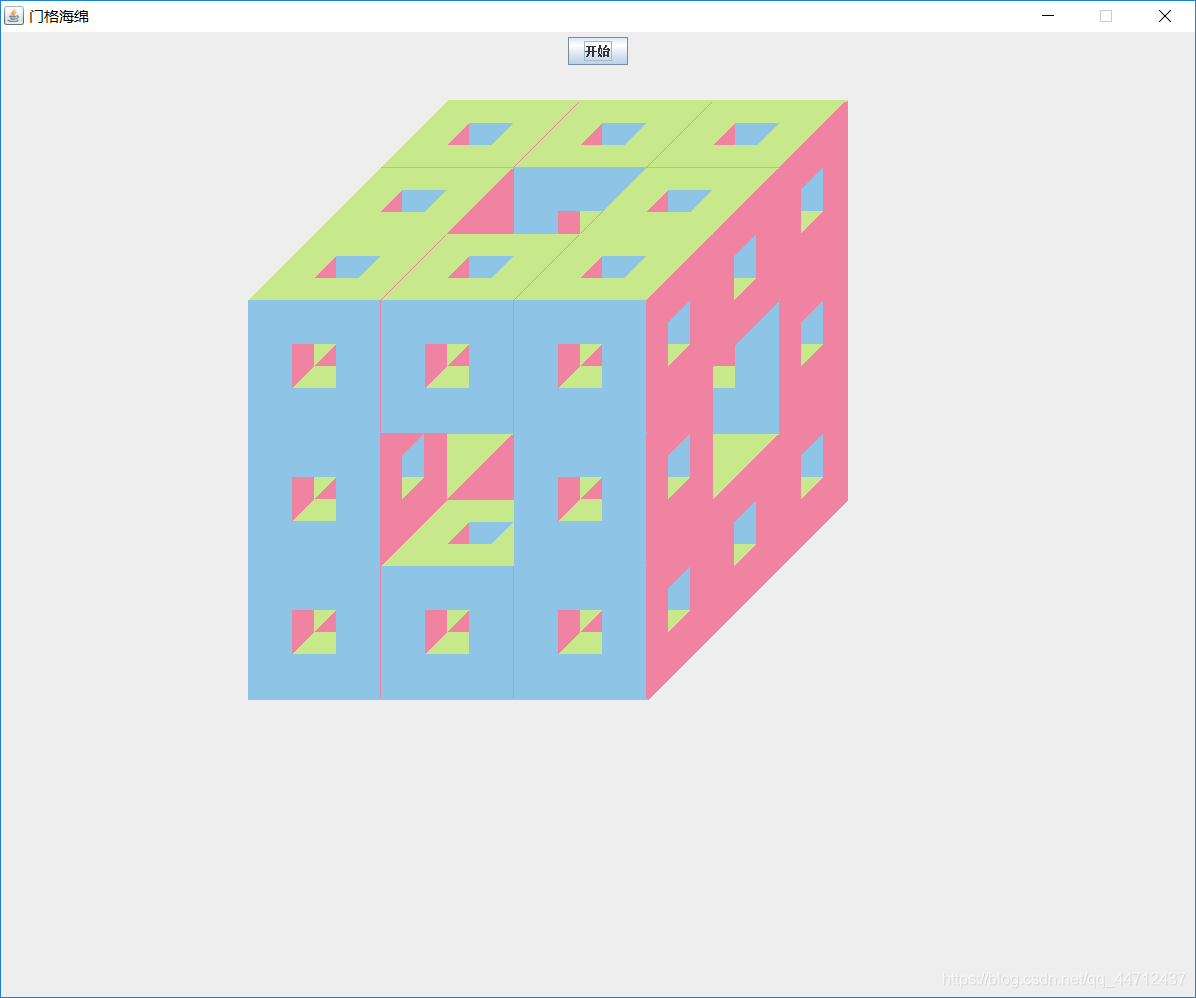
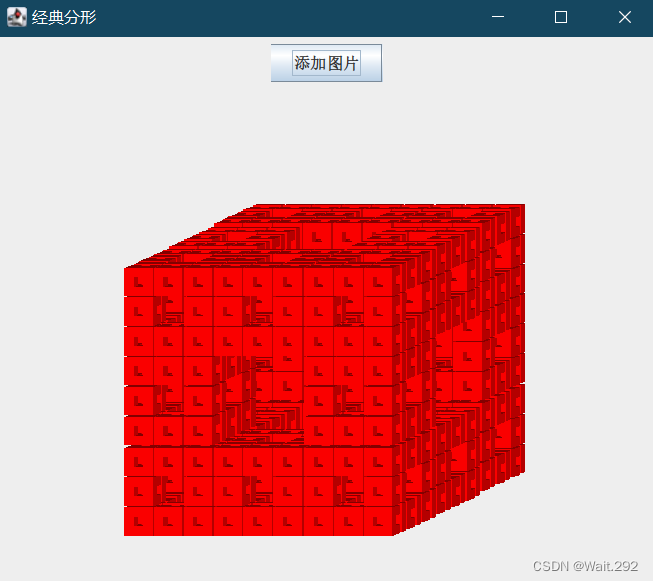
门格海绵（由于没计算好长宽高，看起来不太像立方体，但能凑合）
门格海绵由三层构成，第一层8个，第二层4个，第三层8个。门格海绵并不复杂但较为繁琐这里就不展开来讲了直接放代码

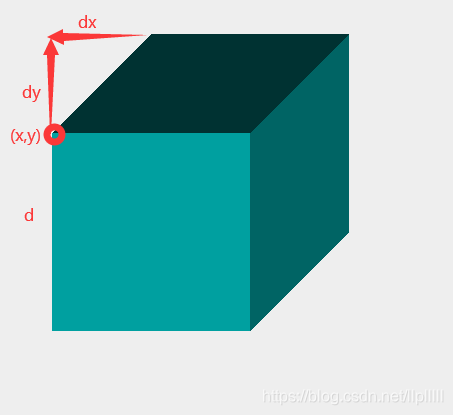
public void smallsquare(Graphics g,int n,int x0,int y0,int a,int dx,int dy){if (n==1){  g.drawRect(x0, y0-a, a, a);g.drawLine(x0+dx, y0-a-dy, x0+dx+a, y0-a-dy);g.drawLine(x0+dx+a, y0-a-dy, x0+dx+a, y0-dy);g.drawLine(x0, y0-a, x0+dx, y0-a-dy);g.drawLine(x0+a, y0-a, x0+dx+a, y0-a-dy);g.drawLine(x0+a, y0, x0+a+dx, y0-dy);Polygon Polg2=new Polygon();Polg2.addPoint(x0, y0-a);Polg2.addPoint(x0+a, y0-a);Polg2.addPoint(x0+dx+a, y0-dy-a);Polg2.addPoint(x0+dx, y0-dy-a);    g.setColor(new Color(255,145,0));g.fillPolygon(Polg2);Polygon Polg1=new Polygon();Polg1.addPoint(x0, y0);Polg1.addPoint(x0+a, y0);Polg1.addPoint(x0+a, y0-a);Polg1.addPoint(x0, y0-a);    g.setColor(new Color(121,45,0));g.fillPolygon(Polg1);Polygon Polg3=new Polygon();Polg3.addPoint(x0+a, y0);Polg3.addPoint(x0+a, y0-a);Polg3.addPoint(x0+a+dx, y0-a-dy);Polg3.addPoint(x0+a+dx, y0-dy);    g.setColor(new Color(137,111,0));g.fillPolygon(Polg3);return;}smallsquare(g,n-1,x0+2*dx/3,y0-2*dy/3,a/3,dx/3,dy/3);smallsquare(g,n-1,x0+2*dx/3+a/3,y0-2*dy/3,a/3,dx/3,dy/3);smallsquare(g,n-1,x0+2*dx/3+2*a/3,y0-2*dy/3,a/3,dx/3,dy/3);  smallsquare(g,n-1,x0+dx/3,y0-dy/3,a/3,dx/3,dy/3);smallsquare(g,n-1,x0+dx/3+2*a/3,y0-dy/3,a/3,dx/3,dy/3);  smallsquare(g,n-1,x0,y0,a/3,dx/3,dy/3);smallsquare(g,n-1,x0+a/3,y0,a/3,dx/3,dy/3);smallsquare(g,n-1,x0+2*a/3,y0,a/3,dx/3,dy/3);smallsquare(g,n-1,x0+2*dx/3,y0-2*dy/3-a/3,a/3,dx/3,dy/3);smallsquare(g,n-1,x0+2*dx/3+2*a/3,y0-2*dy/3-a/3,a/3,dx/3,dy/3);smallsquare(g,n-1,x0,y0-a/3,a/3,dx/3,dy/3);smallsquare(g,n-1,x0+2*a/3,y0-a/3,a/3,dx/3,dy/3);smallsquare(g,n-1,x0+2*dx/3,y0-2*dy/3-2*a/3,a/3,dx/3,dy/3);smallsquare(g,n-1,x0+2*dx/3+a/3,y0-2*dy/3-2*a/3,a/3,dx/3,dy/3);smallsquare(g,n-1,x0+2*dx/3+2*a/3,y0-2*dy/3-2*a/3,a/3,dx/3,dy/3);  smallsquare(g,n-1,x0+dx/3,y0-dy/3-2*a/3,a/3,dx/3,dy/3);smallsquare(g,n-1,x0+dx/3+2*a/3,y0-dy/3-2*a/3,a/3,dx/3,dy/3);  smallsquare(g,n-1,x0,y0-2*a/3,a/3,dx/3,dy/3);smallsquare(g,n-1,x0+a/3,y0-2*a/3,a/3,dx/3,dy/3);smallsquare(g,n-1,x0+2*a/3,y0-2*a/3,a/3,dx/3,dy/3);
}

在mouseReleased(MouseEvent e)函数中

if("门格海绵".equals(name)){Mengersponge sponge=new Mengersponge();sponge.smallsquare(n, 4, 50, 950, 630, 220, 220);
}

当n=4时图案和上图一样

关于画图板内内容差不多到这，实际上是加强的递归的运用。另外画图板还有分形，但由于并不难就不介绍了，下一课讲数组


http://chatgpt.dhexx.cn/article/mk9QIsOT.shtml

相关文章

分形理论中的分维解析

分形理论中的分维解析

最近打算利用一段时间好好学习一下分形理论&#xff0c;也写一系列博客记录下自己的学习归纳情况。下面是这部分文章的目录&#xff1a; 一、分形理论的历史过程 二、分形理论的基础概念 三、分形理论的分维解析 四、分形理论的Hausdorff维数 五、分形理论的盒维数 六、分形理论…
阅读更多...
python绘制n阶科赫曲线线段_分形几何中科赫雪花的绘制

python绘制n阶科赫曲线线段_分形几何中科赫雪花的绘制

目录分形几何在自然界中广泛存在（康托尔集、谢尔滨斯基三角形、门格海绵、龙形曲线、科赫曲线...)，实际上分形几何是一种迭代的几何图形。本文主要讨论科赫曲线。 科赫曲线的绘制： import turtle def koch(size,n):#绘制科赫曲线含俩个参数，大小和阶数 if n == 0:#基线情…
阅读更多...
【计算几何】大自然的数学模型--分形几何

【计算几何】大自然的数学模型--分形几何

一、前言 分形几何是几何数学中的一个分支&#xff0c;也称大自然几何学&#xff0c;由著名数学家本华曼德勃罗&#xff08; 法语&#xff1a;BenoitB.Mandelbrot&#xff09;在 1975 年构思和发展出来的一种新的几何学。分形几何是对大自然中微观与宏观和谐统一之美的发现&…
阅读更多...
Java分形递归——门格海绵

Java分形递归——门格海绵

门格海绵的结构简单来说就是从一个正方体开始&#xff1b;再把正方体的每一个面分成9个正方形&#xff0c;这时就形成了由27个小正方体组成的一个大正方体&#xff1b;然后再把每一面的中间的正方体和最中心的正方体去掉&#xff0c;最终留下20个正方体。最后&#xff0c;把每一…
阅读更多...
门格海绵的实现

门格海绵的实现

实现效果&#xff1a; 源代码&#xff1a; package sponge;import java.awt.Color; import java.awt.Graphics; import java.awt.Graphics2D; import java.awt.Point; import java.awt.Polygon;import javax.swing.JFrame;public class Sponge_Main extends JFrame impleme…
阅读更多...
混沌与分形（一）：谢尔宾斯基三角形与门格海绵

混沌与分形（一）：谢尔宾斯基三角形与门格海绵

研究混沌运动&#xff0c;少不了对分形理论的探讨。分形&#xff1a;通常被定义为“一个粗糙或零碎的几何形状&#xff0c;可以分成数个部分&#xff0c;且每一部分都&#xff08;至少近似地&#xff09;是整体缩小后的形状”&#xff0c;即具有自相似的性质。 本篇将从一维过…
阅读更多...
分形之门格海绵

分形之门格海绵

门格海绵解决思路&#xff1a; 1. 迭代如何实现 2. 立方体该怎么画 3. 实现门格海绵代码 4. 画图板门格海绵代码 1. 迭代如何实现 为了实现从1图—>2图—>3图效果,我们就要想到用迭代去实现. 因为像3图这样的图形,是由若干个2图这样的基本图形组成的 那么,怎样实现…
阅读更多...
JAVA学习日志之门格海绵

JAVA学习日志之门格海绵

门格海绵的结构可以用以下方法形象化&#xff1a; 从一个正方体开始。&#xff08;第一个图像&#xff09; 把正方体的每一个面分成9个正方形。这将把正方体分成27个小正方体&#xff0c;像魔方一样。 把每一面的中间的正方体去掉&#xff0c;把最中心的正方体也去掉&#xff0…
阅读更多...
复杂分形，简单规则：门格海绵世界探秘

复杂分形，简单规则：门格海绵世界探秘

连绵的山川、飘浮的云朵、岩石的断裂口、布朗粒子运动的轨迹、树冠、花菜、大脑皮层……这些部分与整体以某种方式相似的形体&#xff0c;可以说&#xff0c;就是“分形”的要义了&#xff0c;也恰恰是这些“不规则的”、“分散的”、“支离破碎的”物体又重新让我们认识了自然…
阅读更多...
JQData | 高校版使用教程，30秒安装完成，自带Python环境

JQData | 高校版使用教程，30秒安装完成，自带Python环境

本地量化金融数据JQData&#xff0c;是聚宽数据团队专门为金融机构、学术团体和量化研究者们提供的本地量化金融数据服务。自有版权&#xff0c;支持国内多家头部券商实盘交易。历经15万量化研究者与数百家机构使用验证。 JQData目前已支持国内30 高校&#xff0c;本次更新&…
阅读更多...
JQData + matplotlib 实现回测日志的交易细节可视化 量化数据接口

JQData + matplotlib 实现回测日志的交易细节可视化 量化数据接口

原文&#xff1a;https://zhuanlan.zhihu.com/p/49051899 前言&#xff1a; 做量化交易的朋友都知道回测的重要性&#xff0c;回测结果是衡量一个量化交易策略是否靠谱的重要依据。回测平台会按历史行情数据模拟成交&#xff0c;并将回测结果汇总成报告。 在很多时候&#xf…
阅读更多...
Note: Python学习笔记 -- Anaconda install jqdata

Note: Python学习笔记 -- Anaconda install jqdata

运行代码下列代码&#xff0c;提示错误 没有安装 jqdata。打开Anaconda Prompt 输入 pip install jqdata 提示cannot find command git然后百度了半天&#xff0c;有人说 pip install git 出错可以使用 conda install git 但是依然出错。最后去官网下载了Git:https://git-scm.…
阅读更多...
jq使用教程01_最贴心教程，安装JQData全靠这篇指南

jq使用教程01_最贴心教程，安装JQData全靠这篇指南

Hi, 各位亲爱的小伙伴们&#xff01; 近来听说有部分小伙伴在安装JQData时遇到了点小麻烦&#xff0c;导致最后没有安装成功&#xff0c;为了帮助小伙伴们快速成功安装JQData&#xff0c;小编今天来为大家排一下“雷”&#xff0c;希望能帮到你们哟 (&#xff65;ω&#xff6…
阅读更多...
事件驱动的选股小工具（JQData）

事件驱动的选股小工具（JQData）

昨天发改委下发了《关于积极推进风电、光伏发电无补贴平价上网有关工作的通知》&#xff0c;也不知道对股市是利空还是利多。连夜做了一个搜索公司经营范围的小工具,看看那些股票受到影响。 以后还可以增加筛选条件&#xff0c;比如财务指标&#xff0c;剔除ST股票&#xff0c;…
阅读更多...
股票python量化交易008-JoinQuant中JQData的使用

股票python量化交易008-JoinQuant中JQData的使用

查阅JoinQuant中JQData的使用文档python代码实现导入JQData，并认证用户身份。认证完毕显示“auth success”后即可使用 from jqdatasdk import *; auth(ID,Password);#ID是申请时所填写的手机号；Password为聚宽官网登录密码 # 查询jqdata的调用次数情况 surplus_count = g…
阅读更多...
jqdata pyechart： 用grid双图实现k线带图成交 — by QUANTAXIS

jqdata pyechart： 用grid双图实现k线带图成交 — by QUANTAXIS

from jqdatasdk import * from pyecharts import Kline,Bar,Grid 首先我们先应JQDATA 的活动演示一下如何调用pyecharts 画图 auth(acc,password) dataget_price(000001.XSHE) auth success先打印下 data 我们可以看到 jqdata返回的格式是 一个单index的Dataframe data.he…
阅读更多...
Quant | JQData使用API简单梳理（二）

Quant | JQData使用API简单梳理（二）

聚宽平台实际上提供了两种查询数据的方法，第一种是线上在聚宽平台可以使用的API：jqdata，另外一种则是本地的接口：JQData，是的，你没有看错，只是大小写的不同，搞得一开始我以为完全是同一种。jqdata可以线上通过import jqdata来引入数据接口，本地的JQData则是通过import…
阅读更多...
jqdata(data是什么文件格式)

jqdata(data是什么文件格式)

期货交易中bar和tick是什么意思 Bar 的概念 在一定时间段内的时间序列就构成了一根 K 线(日本蜡烛图)&#xff0c;单根 K 线被称为 Bar。 如果是一分钟内的 Tick 序列&#xff0c;即构成一根分钟 K 线&#xff0c;又称分钟 Bar; 如果是一天内的分钟序列&#xff0c;即构成一根日…
阅读更多...
JQData | 量化界最好用的本地量化金融数据（free free~）

JQData | 量化界最好用的本地量化金融数据（free free~）

什么是本地量化金融数据 - JQData &#xff1f; 使用JQData本地量化金融数据服务&#xff0c;可快速查看、计算或接入金融数据信息&#xff0c;解决本地、web、自研金融终端调用数据的需求。支持python多版本及多操作系统。为财经类企业、金融机构、学术研究机构和量化爱好者们…
阅读更多...
获取股票数据【使用JQData查询行情数据、财务指标、估值指标】

获取股票数据【使用JQData查询行情数据、财务指标、估值指标】

了解股票&#xff1a; 在上一次量化小科普【什么是量化&#xff1f;常用的股票量化指标、如何搭建量化交易系统】对于量化的概念有了一个基本认识&#xff0c;其中量化的主体在这门课程的学习中是“股票”&#xff0c;而当别人问你&#xff1a;“什么是股票&#xff1f;”&…
阅读更多...
推荐文章

Copyright @ 2022~2023