门格海绵的结构简单来说就是从一个正方体开始;再把正方体的每一个面分成9个正方形,这时就形成了由27个小正方体组成的一个大正方体;然后再把每一面的中间的正方体和最中心的正方体去掉,最终留下20个正方体。最后,把每一个留下的小正方体都重复前面的步骤。把以上的步骤重复无穷多次以后,得到的图形就是门格海绵。演变过程如下所示:


在实际代码编程时的思路是将一个门格海绵分为上中下三层,如图:
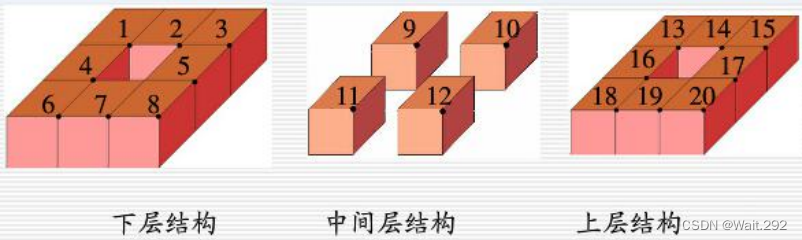
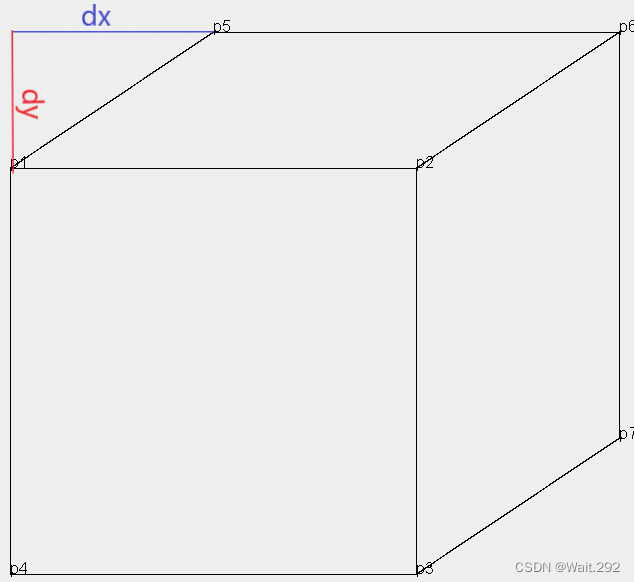
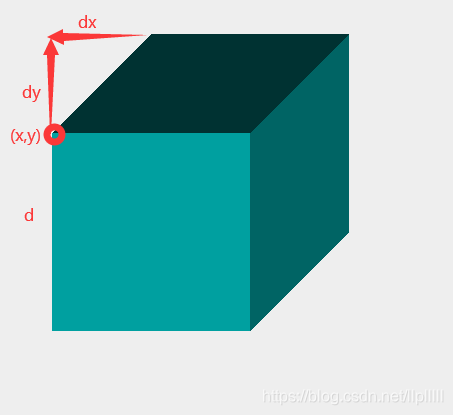
如图,将立方体7个顶点依次用p1,p2,p3,p4,p5,p6,p7表示;dx,dy是透视偏移量,立方体的边长设为d。
基础值设置好后,就可以开始画第一个立方体。绘制思路:通过设置一个立方体顶点的坐标来确定需要的其他六个顶点的坐标,然后画出一个立方体,再将该立方体分为20个小立方体,每个小立方体同样是通过顶点坐标的信息,递归调用画图方法绘制出来的。
第一步,先画出一个立方体的线框,给三个面填充颜色。
常规操作,显示一个界面,添加按钮;
package menggehaimian;import java.awt.FlowLayout;
import java.awt.Graphics;
import javax.swing.JButton;
import javax.swing.JFrame;public class menggehaimian1 extends JFrame {public void initUI(){this.setSize(500,600);this.setTitle("经典分形");this.setDefaultCloseOperation(3);FlowLayout fl = new FlowLayout();this.setLayout(fl);//加上按钮JButton buDraw = new JButton("添加图片");this.add(buDraw);//加监听器this.setVisible(true);//获取画布,一定在界面可见之后Graphics g = this.getGraphics();DrawLisMGHM1 dl = new DrawLisMGHM1(g);buDraw.addActionListener(dl);}public static void main(String[] args) {menggehaimian1 lu=new menggehaimian1();lu.initUI();}
}在监听器类中实现具体的方法:
package menggehaimian;import java.awt.Color;
import java.awt.Graphics;
import java.awt.Polygon;
import java.awt.event.ActionEvent;
import java.awt.event.ActionListener;
//画图按钮的监听器,点一下画个东西出来
public class DrawLisMGHM1 implements ActionListener{private Graphics g;public DrawLisMGHM1(Graphics g) {this.g=g;}//画门格海绵//1.画一个线框 2.立体:w h参数@Overridepublic void actionPerformed(ActionEvent arg0) {//根据给定的三组参数,画一个立方体线框:int dx=150,dy=100;int x1=20,y1=200;int d=300;int x2=x1+d,y2=y1;int x3=x2,y3=y2+d;int x4=x1,y4=y1+d;int x5=x1+dx,y5=y1-dy;int x6=x5+d,y6=y5;int x7=x6,y7=y6+d;g.drawLine(x1, y1, x2, y2);g.drawString("p1", x1, y1);g.drawLine(x2, y2, x3, y3);g.drawString("p2", x2, y2);g.drawLine(x3, y3, x4, y4);g.drawString("p3", x3, y3);g.drawLine(x4, y4, x1, y1);g.drawString("p4", x4, y4);g.drawLine(x1, y1, x5, y5);g.drawString("p5", x5, y5);g.drawLine(x5, y5, x6, y6);g.drawString("p6", x6, y6);g.drawLine(x6, y6, x2, y2);g.drawLine(x6, y6, x7, y7);g.drawString("p7", x7, y7);g.drawLine(x7, y7, x3, y3); //填充面Polygon pon1 = new Polygon();//创建一个多边形用来填充pon1.addPoint(x1, y1);pon1.addPoint(x5, y5);pon1.addPoint(x6, y6);pon1.addPoint(x2, y2);g.setColor(new Color(210,0,0));g.fillPolygon(pon1);Polygon pon2 = new Polygon();//创建一个多边形用来填充pon2.addPoint(x1, y1);pon2.addPoint(x2, y2);pon2.addPoint(x3, y3);pon2.addPoint(x4, y4);g.setColor(new Color(180,0,0));g.fillPolygon(pon2);Polygon pon3 = new Polygon();//创建一个多边形用来填充pon3.addPoint(x2, y2);pon3.addPoint(x6, y6);pon3.addPoint(x7, y7);pon3.addPoint(x3, y3);g.setColor(new Color(100,0,0));g.fillPolygon(pon3);}
}
如图,首先画出第一个正方形;接下来 我们加入递归算法,依次画出其他的立方体。和上面的代码差不多,需要先确定几个固定参数。在这个参数里需要多加一个count参数,控制递归的次数。
public void actionPerformed(ActionEvent e) {//根据给定的三组参数,画一个立方体线框:int x=150,y=200,d=200,dx=100,dy=50,count = 1;//count可以设置递归的次数Menger_Sponge(x, y, d, dx, dy, count);}其次,通过顶点坐标获取到其他顶点的坐标的方法;在这里,我用p0表示为顶点,表示出其他6个点的坐标。利用条件if(){}else{}语句,表示出下中上三层每个小方块的首地址,并填充颜色。
private void Menger_Sponge(int x, int y, int d, int dx, int dy, int count) {// 记录单个方块7个顶角的坐标Point p0 = new Point(x, y);Point p1 = new Point(p0.x + d, p0.y);Point p2 = new Point(p1.x, p1.y + d);Point p3 = new Point(p2.x - d, p2.y);Point p4 = new Point(p0.x + dx, p0.y - dy);Point p5 = new Point(p1.x + dx, p1.y - dy);Point p6 = new Point(p2.x + dx, p2.y - dy);count--; //递归次数减1if (count >= 0) {//递归到底层各小方块的首地址Menger_Sponge(p0.x + 2 * dx / 3, p0.y - 2 * dy / 3 + 2 * d / 3, d / 3, dx / 3, dy / 3, count);Menger_Sponge(p0.x + 2 * dx / 3 + d / 3, p0.y - 2 * dy / 3 + 2 * d / 3, d / 3, dx / 3, dy / 3, count);Menger_Sponge(p0.x + 2 * dx / 3 + 2 * d / 3, p0.y - 2 * dy / 3 + 2 * d / 3, d / 3, dx / 3, dy / 3, count);Menger_Sponge(p0.x + dx / 3, p0.y - dy / 3 + 2 * d / 3, d / 3, dx / 3, dy / 3, count);Menger_Sponge(p0.x + dx / 3 + 2 * d / 3, p0.y - dy / 3 + 2 * d / 3, d / 3, dx / 3, dy / 3, count);Menger_Sponge(p0.x, p0.y + 2 * d / 3, d / 3, dx / 3, dy / 3, count);Menger_Sponge(p0.x + d / 3, p0.y + 2 * d / 3, d / 3, dx / 3, dy / 3, count);Menger_Sponge(p0.x + 2 * d / 3, p0.y + 2 * d / 3, d / 3, dx / 3, dy / 3, count);//递归到中层各小方块的首地址Menger_Sponge(p0.x + 2 * dx / 3, p0.y - 2 * dy / 3 + d / 3, d / 3, dx / 3, dy / 3, count);Menger_Sponge(p0.x + 2 * dx / 3 + 2 * d / 3, p0.y - 2 * dy / 3 + d / 3, d / 3, dx / 3, dy / 3, count);Menger_Sponge(p0.x, p0.y + d / 3, d / 3, dx / 3, dy / 3, count);Menger_Sponge(p0.x + 2 * d / 3, p0.y + d / 3, d / 3, dx / 3, dy / 3, count);//递归到顶层各小方块的首地址Menger_Sponge(p0.x + 2 * dx / 3, p0.y - 2 * dy / 3, d / 3, dx / 3, dy / 3, count);Menger_Sponge(p0.x + 2 * dx / 3 + d / 3, p0.y - 2 * dy / 3, d / 3, dx / 3, dy / 3, count);Menger_Sponge(p0.x + 2 * dx / 3 + 2 * d / 3, p0.y - 2 * dy / 3, d / 3, dx / 3, dy / 3, count);Menger_Sponge(p0.x + dx / 3, p0.y - dy / 3, d / 3, dx / 3, dy / 3, count);Menger_Sponge(p0.x + dx / 3 + 2 * d / 3, p0.y - dy / 3, d / 3, dx / 3, dy / 3, count);Menger_Sponge(p0.x, p0.y, d / 3, dx / 3, dy / 3, count);Menger_Sponge(p0.x + d / 3, p0.y, d / 3, dx / 3, dy / 3, count);Menger_Sponge(p0.x + 2 * d / 3, p0.y, d / 3, dx / 3, dy / 3, count);}else {//填充正面矩形Polygon poly1 = new Polygon();poly1.addPoint(p0.x, p0.y);poly1.addPoint(p1.x, p1.y);poly1.addPoint(p2.x, p2.y);poly1.addPoint(p3.x, p3.y);g.setColor(new Color(250, 0, 0));g.fillPolygon(poly1);//填充右面矩形Polygon poly2 = new Polygon();poly2.addPoint(p1.x, p1.y);poly2.addPoint(p2.x, p2.y);poly2.addPoint(p6.x, p6.y);poly2.addPoint(p5.x, p5.y);g.setColor(new Color(180, 0, 0));g.fillPolygon(poly2);//填充上面矩形Polygon poly3 = new Polygon();poly3.addPoint(p0.x, p0.y);poly3.addPoint(p1.x, p1.y);poly3.addPoint(p5.x, p5.y);poly3.addPoint(p4.x, p4.y);g.setColor(new Color(130, 0, 0));g.fillPolygon(poly3);}}
}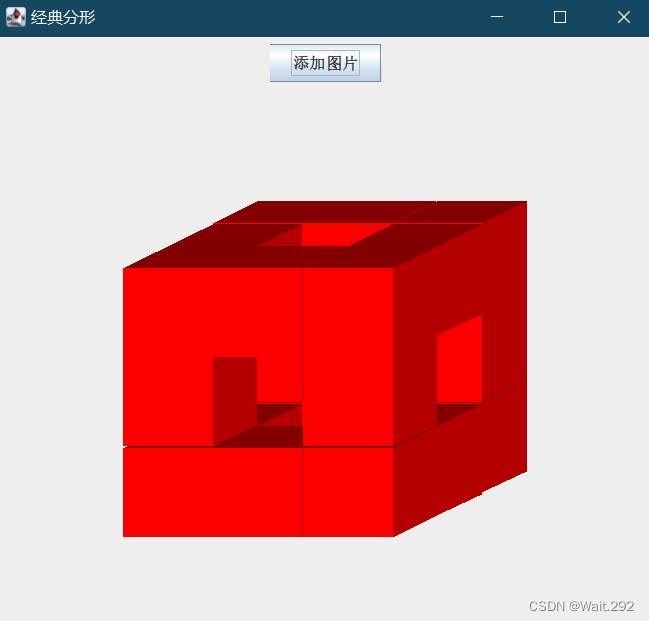
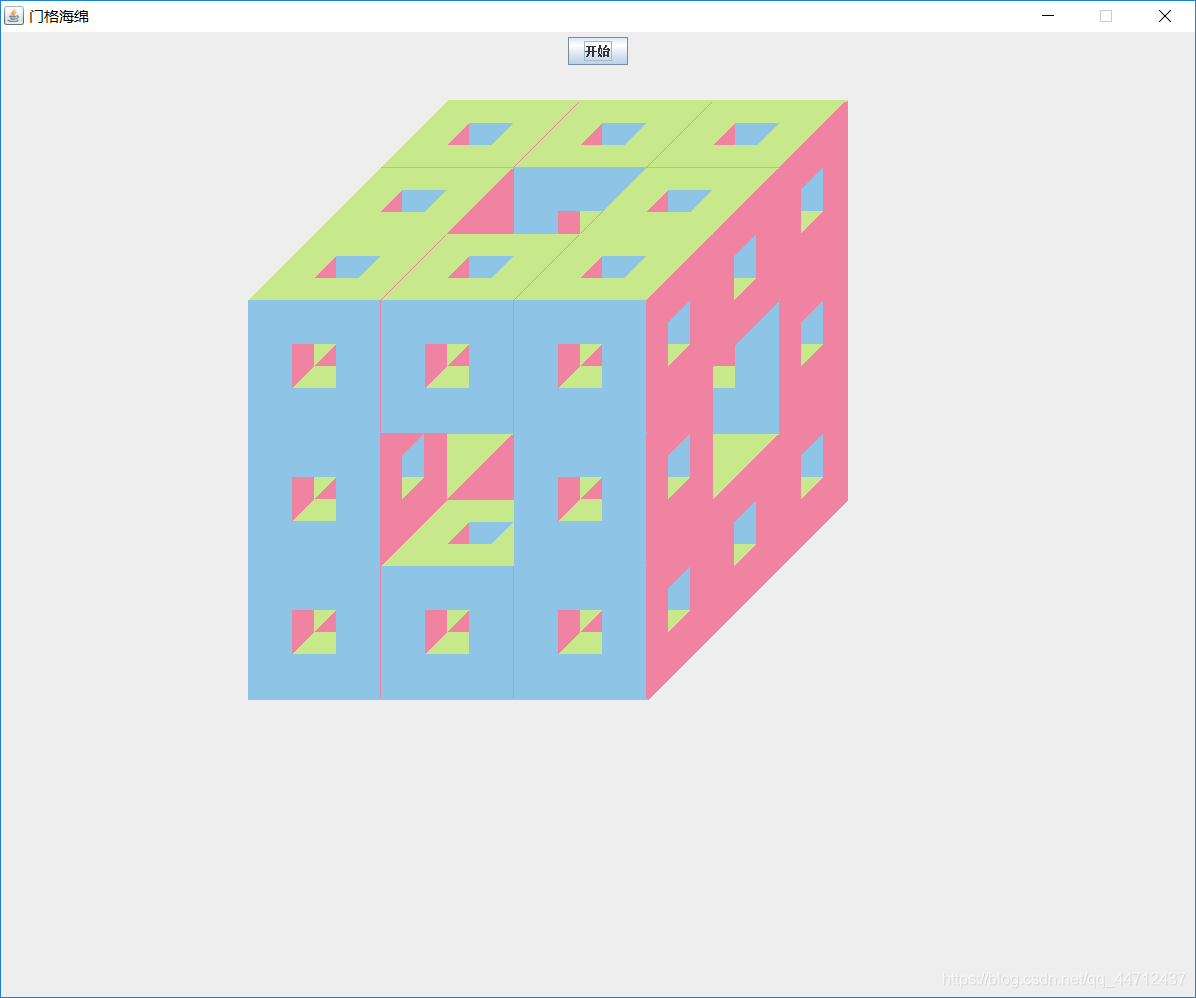
由此就得到了第一个由20个小立方体构成的大立方体。将count的递归次数改为3,就得到了由该立方体递归分形三次后所得的图形,也就是门格海绵。
int x=100,y=200,d=200,dx=100,dy=50,count = 3;
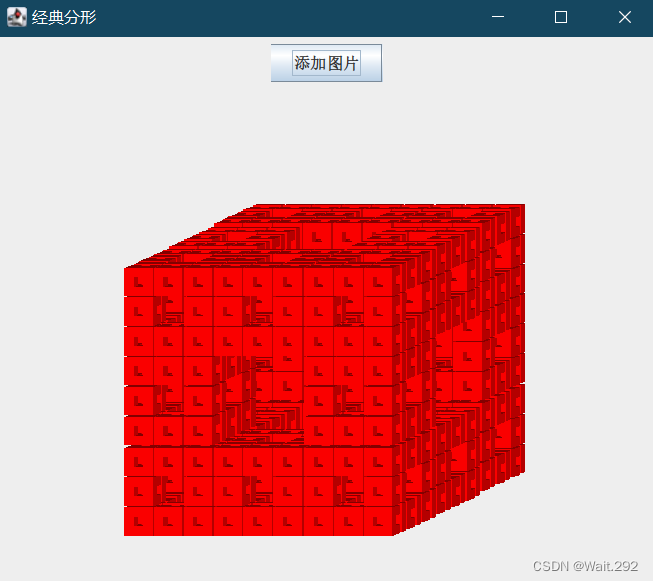
总结:思路并不难,但是因为代码多,坐标定位比较考察数学模型思维,容易忽略某些细节,还有各个代码之间的调试,出现bug找出来也很难,要一步一步,从小细节慢慢找,慢慢检查。以后碰到更复杂的实现过程时,就更要注意。