JAVA学习日志之门格海绵

article/2025/1/7 6:42:23

门格海绵的结构可以用以下方法形象化：
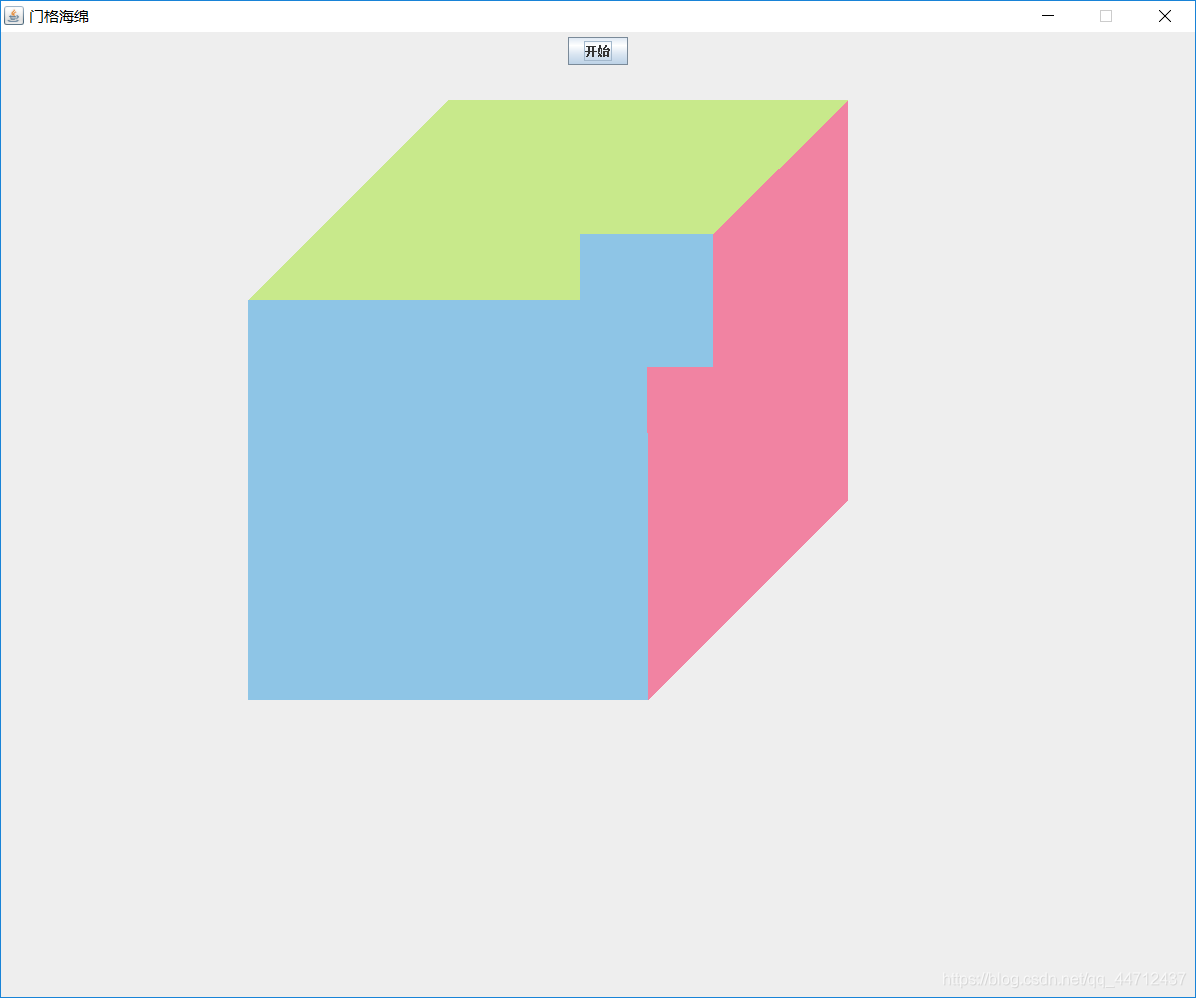
从一个正方体开始。（第一个图像）
把正方体的每一个面分成9个正方形。这将把正方体分成27个小正方体，像魔方一样。
把每一面的中间的正方体去掉，把最中心的正方体也去掉，留下20个正方体（第二个图像）。
把每一个留下的小正方体都重复第1-3个步骤。
把以上的步骤重复无穷多次以后，得到的图形就是门格海绵。
在这里插入图片描述

实际写代码的时候思路是将一个门格海绵分为三层绘制，解析图如下：
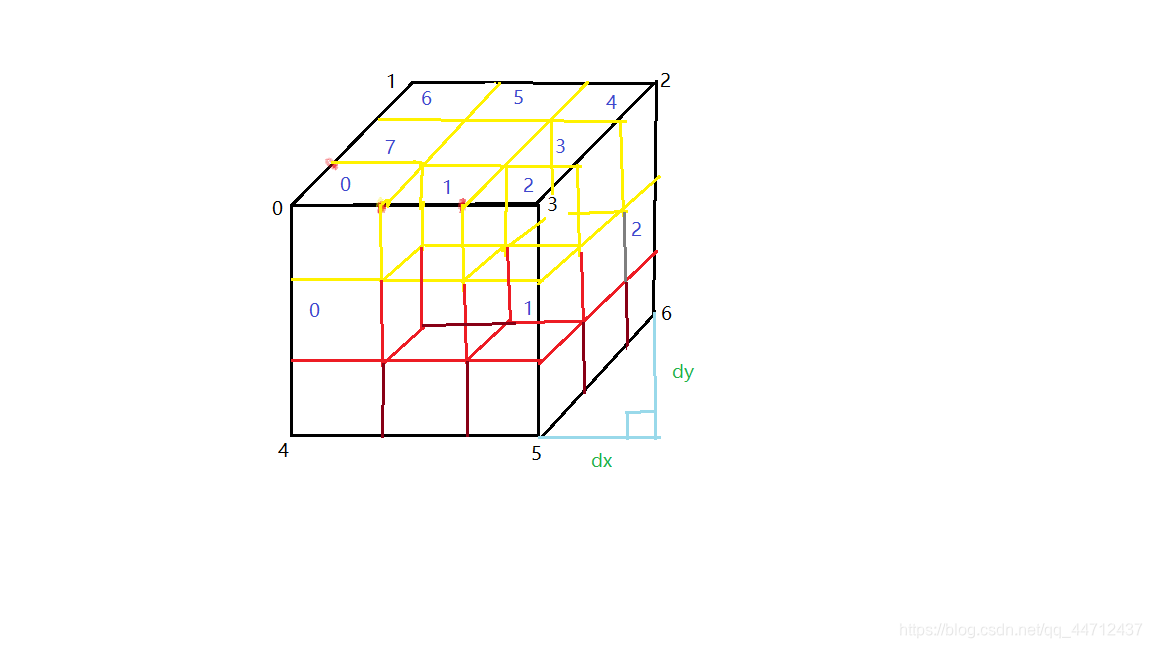
在这里插入图片描述
黑色数字代表立方体的顶点，只需要7个就够了；蓝色数字用来标记小立方体，第二层立方体用红色标识，第三层用褐色标识，dx,dy是透视偏移量，立方体的边长设为d.
思路：通过设置一个立方体顶点的坐标来确定需要的其他六个坐标，然后画出一个立方体，再将该立方体分为20个小立方体，每个小立方体同样是通过顶点坐标的信息，递归调用画图方法绘制出来的。每个小立方体都是一个大立方体的缩小。

第一步：实现通过顶点坐标获取到其他顶点的坐标的方法 getpointbyp0();在这里，我用p0表示为顶点。
我是以每个立方体的0号点为顶点。

public Point[] getpointbyp0(Point p0,int d,int dx,int dy){Point[] ps = new Point[7];ps[0] = p0;ps[1] = new Point(p0.x+dx,p0.y-dy);ps[2] = new Point(p0.x+d+dx,p0.y-dy);ps[3] = new Point(p0.x+d,p0.y);ps[4] = new Point(p0.x,p0.y+d);ps[5] = new Point(p0.x+d,p0.y+d);ps[6] = new Point(p0.x+d+dx,p0.y-dy+d);return ps;

这个方法返回的是一个包含了7个顶点信息的点数组，顶点为数组的第一个元素。

第二步：递归画法

public void drawMenGe(Point p,int d,int dx,int dy, int count){if(count<=0)return;count--;Point[] ps = getpointbyp0(p, d, dx, dy);//画立方体Polygon ponlygon1 = new Polygon();ponlygon1.addPoint(ps[0].x,ps[0].y);ponlygon1.addPoint(ps[1].x,ps[1].y);ponlygon1.addPoint(ps[2].x,ps[2].y);ponlygon1.addPoint(ps[3].x,ps[3].y);g.setColor(new Color(200,233,139));g.fillPolygon(ponlygon1); Polygon ponlygon2 = new Polygon();ponlygon2.addPoint(ps[0].x,ps[0].y);ponlygon2.addPoint(ps[3].x,ps[3].y);ponlygon2.addPoint(ps[5].x,ps[5].y);ponlygon2.addPoint(ps[4].x,ps[4].y);g.setColor(new Color(142,197,230));g.fillPolygon(ponlygon2); Polygon ponlygon3 = new Polygon();ponlygon3.addPoint(ps[2].x,ps[2].y);ponlygon3.addPoint(ps[3].x,ps[3].y);ponlygon3.addPoint(ps[5].x,ps[5].y);ponlygon3.addPoint(ps[6].x,ps[6].y);g.setColor(new Color(241,131,162));g.fillPolygon(ponlygon3);

这一段是完成画立方体的，Point[] ps = getpointbyp0(p, d, dx, dy); 这一步得到了立方体的所有顶点信息，然后将立方体的三个面涂上颜色。
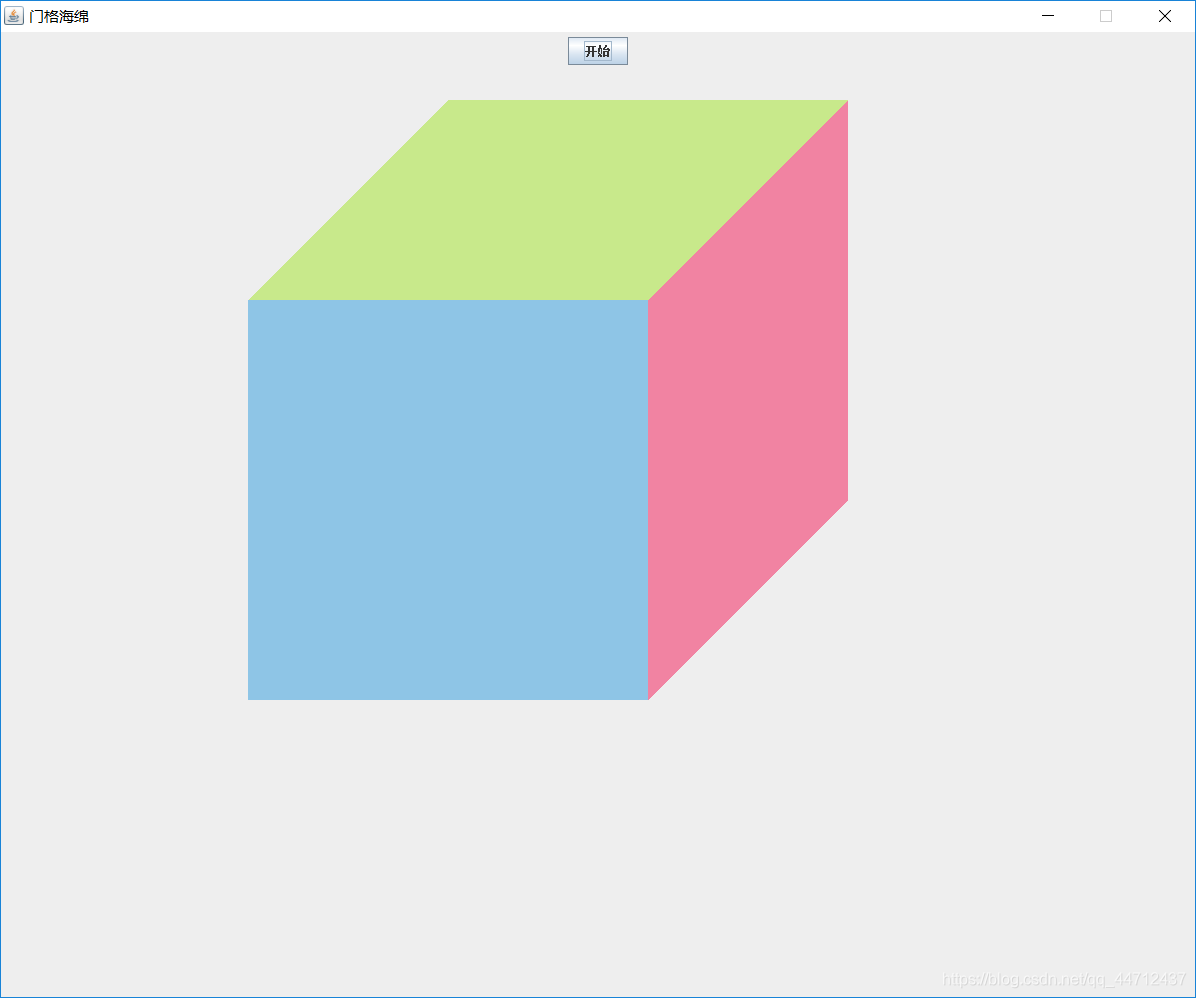
在这里插入图片描述
0123 表示的是上面，0354表示的是前面，2356表示的是侧面。
那现在要做的就是将这个完整的立方体分成20个小立方体，每个小立方体的7个顶点信息都存在一个顶点数组里，接着调用递归方法就可以画出来每个小立方体。

//第一层Point pp1[] = new Point[8];pp1[0] = new Point(p.x,p.y);pp1[1] = new Point(p.x+d/3,p.y);pp1[2] = new Point(p.x+2*d/3,p.y);pp1[3] = new Point(p.x+2*d/3+dx/3,p.y-dy/3);pp1[4] = new Point(p.x+2*d/3+dx*2/3,p.y-dy*2/3);pp1[5] = new Point(p.x+d/3+dx*2/3,p.y-dy*2/3);pp1[6] = new Point(p.x+dx*2/3,p.y-dy*2/3);pp1[7] = new Point(p.x+dx/3,p.y-dy/3);drawMenGe(pp1[0],d/3,dx/3,dy/3,count);drawMenGe(pp1[1],d/3,dx/3,dy/3,count);drawMenGe(pp1[2],d/3,dx/3,dy/3,count);drawMenGe(pp1[3],d/3,dx/3,dy/3,count);drawMenGe(pp1[4],d/3,dx/3,dy/3,count);drawMenGe(pp1[5],d/3,dx/3,dy/3,count);drawMenGe(pp1[6],d/3,dx/3,dy/3,count);drawMenGe(pp1[7],d/3,dx/3,dy/3,count);

//第二层Point pp2[] = new Point[4];pp2[0] = new Point(p.x,p.y+d/3);pp2[1] = new Point(p.x+2*d/3,p.y+d/3);pp2[2] = new Point(p.x+2*d/3+dx*2/3,p.y-dy*2/3+d/3);pp2[3] = new Point(p.x+dx*2/3,p.y-dy*2/3+d/3);drawMenGe(pp2[0],d/3,dx/3,dy/3,count);drawMenGe(pp2[1],d/3,dx/3,dy/3,count);drawMenGe(pp2[2],d/3,dx/3,dy/3,count);drawMenGe(pp2[3],d/3,dx/3,dy/3,count);

//第三层Point pp3[] = new Point[8];pp3[0] = new Point(p.x,p.y+2*d/3);pp3[1] = new Point(p.x+d/3,p.y+2*d/3);pp3[2] = new Point(p.x+2*d/3,p.y+2*d/3);pp3[3] = new Point(p.x+2*d/3+dx/3,p.y-dy/3+2*d/3);pp3[4] = new Point(p.x+2*d/3+dx*2/3,p.y-dy*2/3+2*d/3);pp3[5] = new Point(p.x+d/3+dx*2/3,p.y-dy*2/3+2*d/3);pp3[6] = new Point(p.x+dx*2/3,p.y-dy*2/3+2*d/3);pp3[7] = new Point(p.x+dx/3,p.y-dy/3+2*d/3);drawMenGe(pp3[0],d/3,dx/3,dy/3,count);drawMenGe(pp3[1],d/3,dx/3,dy/3,count);drawMenGe(pp3[2],d/3,dx/3,dy/3,count);drawMenGe(pp3[3],d/3,dx/3,dy/3,count);drawMenGe(pp3[4],d/3,dx/3,dy/3,count);drawMenGe(pp3[5],d/3,dx/3,dy/3,count);drawMenGe(pp3[6],d/3,dx/3,dy/3,count);drawMenGe(pp3[7],d/3,dx/3,dy/3,count);

第一层和第三层都只有8个立方体，第二层只有4个立方体。按图上的标识方法，三层的各个小立方体的0号顶点坐标都可以由大立方体的0号坐标计算得到。而且第一层和第三层的标识立方体的方法是一样的，所以第三层的各个小立方体的0号顶点坐标只需要在第一层的基础上给纵坐标加上某个偏移量就够了。找准哪个小立方体是搭在哪个小立方体上的就可以很容易的算出来顶点坐标。不过特殊的地方在不是每个小立方体都能在图上显示出来，会被遮盖，计算时还有画图的时候递归顺序需要注意，否则图形就会出现类似下面的错误。
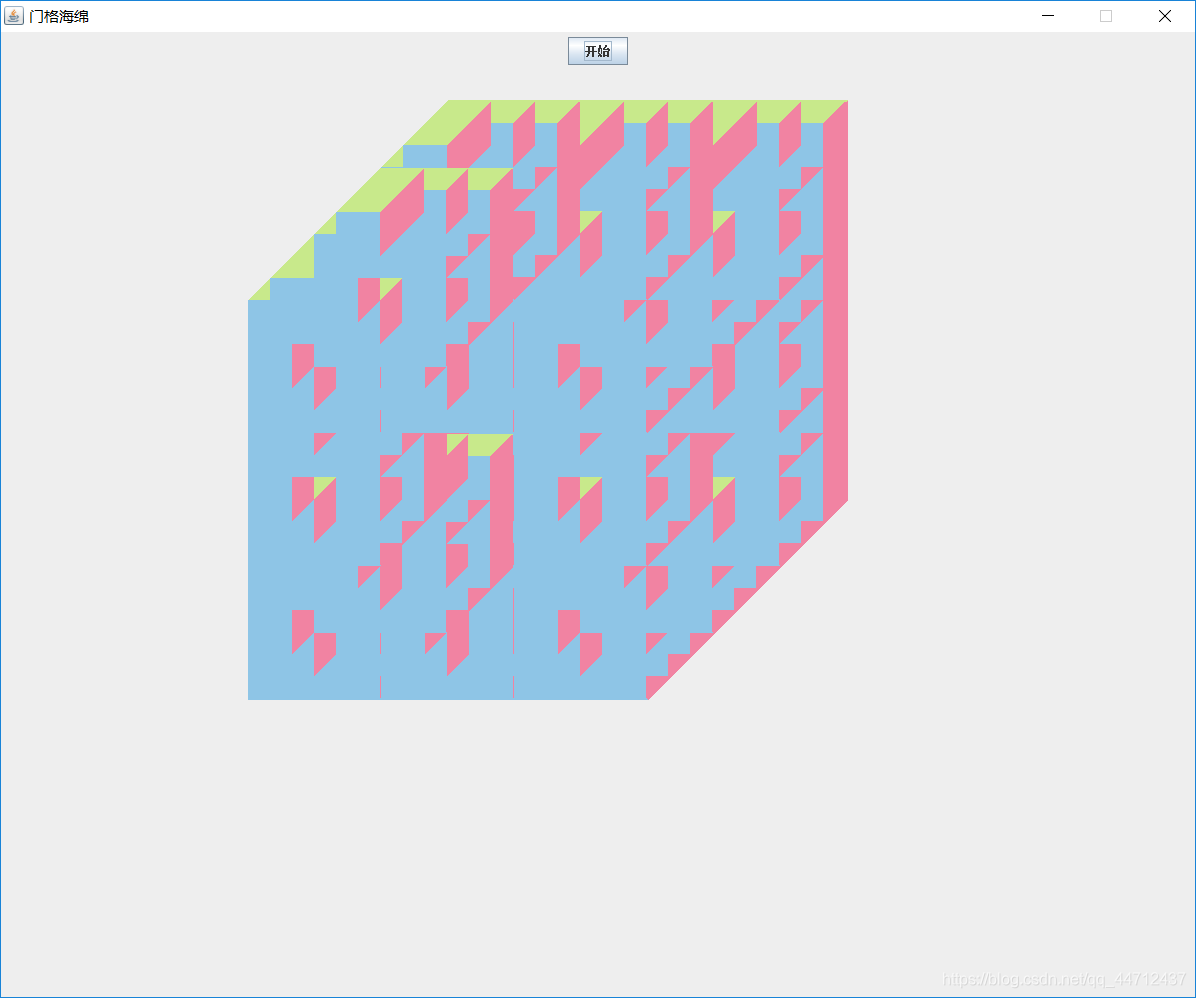
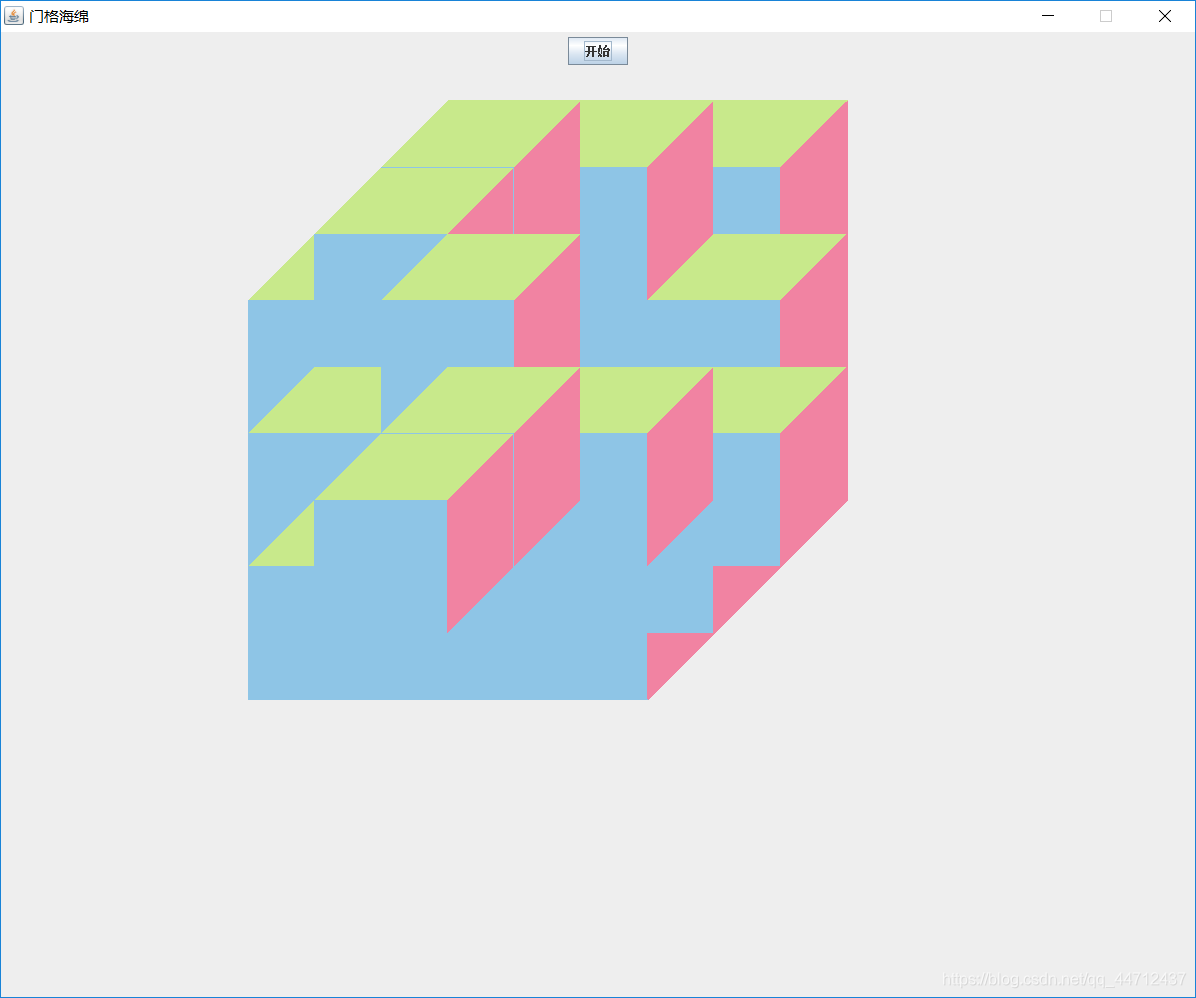
在这里插入图片描述
在这里插入图片描述
图形大小都是对的，只是颜色的填充位置错误。
这就是因为发生了覆盖。

//错误代码//第一层Point pp1[] = new Point[8];pp1[0] = new Point(p.x,p.y);pp1[1] = new Point(p.x+d/3,p.y);pp1[2] = new Point(p.x+2*d/3,p.y);pp1[3] = new Point(p.x+2*d/3+dx/3,p.y-dy/3);pp1[4] = new Point(p.x+2*d/3+dx*2/3,p.y-dy*2/3);pp1[5] = new Point(p.x+d/3+dx*2/3,p.y-dy*2/3);pp1[6] = new Point(p.x+dx*2/3,p.y-dy*2/3);pp1[7] = new Point(p.x+dx/3,p.y-dy/3);drawMenGe(pp1[0],d/3,dx/3,dy/3,count);drawMenGe(pp1[1],d/3,dx/3,dy/3,count);drawMenGe(pp1[2],d/3,dx/3,dy/3,count);drawMenGe(pp1[3],d/3,dx/3,dy/3,count);drawMenGe(pp1[4],d/3,dx/3,dy/3,count);drawMenGe(pp1[5],d/3,dx/3,dy/3,count);drawMenGe(pp1[6],d/3,dx/3,dy/3,count);drawMenGe(pp1[7],d/3,dx/3,dy/3,count);//第二层Point pp2[] = new Point[4];pp2[0] = new Point(p.x,p.y+d/3);pp2[1] = new Point(p.x+2*d/3,p.y+d/3);pp2[2] = new Point(p.x+2*d/3+dx*2/3,p.y-dy*2/3+d/3);pp2[3] = new Point(p.x+dx*2/3,p.y-dy*2/3+d/3);drawMenGe(pp2[0],d/3,dx/3,dy/3,count);drawMenGe(pp2[1],d/3,dx/3,dy/3,count);drawMenGe(pp2[2],d/3,dx/3,dy/3,count);drawMenGe(pp2[3],d/3,dx/3,dy/3,count);//第三层Point pp3[] = new Point[8];pp3[0] = new Point(p.x,p.y+2*d/3);pp3[1] = new Point(p.x+d/3,p.y+2*d/3);pp3[2] = new Point(p.x+2*d/3,p.y+2*d/3);pp3[3] = new Point(p.x+2*d/3+dx/3,p.y-dy/3+2*d/3);pp3[4] = new Point(p.x+2*d/3+dx*2/3,p.y-dy*2/3+2*d/3);pp3[5] = new Point(p.x+d/3+dx*2/3,p.y-dy*2/3+2*d/3);pp3[6] = new Point(p.x+dx*2/3,p.y-dy*2/3+2*d/3);pp3[7] = new Point(p.x+dx/3,p.y-dy/3+2*d/3);drawMenGe(pp3[0],d/3,dx/3,dy/3,count);drawMenGe(pp3[1],d/3,dx/3,dy/3,count);drawMenGe(pp3[2],d/3,dx/3,dy/3,count);drawMenGe(pp3[3],d/3,dx/3,dy/3,count);drawMenGe(pp3[4],d/3,dx/3,dy/3,count);drawMenGe(pp3[5],d/3,dx/3,dy/3,count);drawMenGe(pp3[6],d/3,dx/3,dy/3,count);drawMenGe(pp3[7],d/3,dx/3,dy/3,count);

当你以这种方式画就会出错。

当我们画0号小立方体时，是这样的效果：
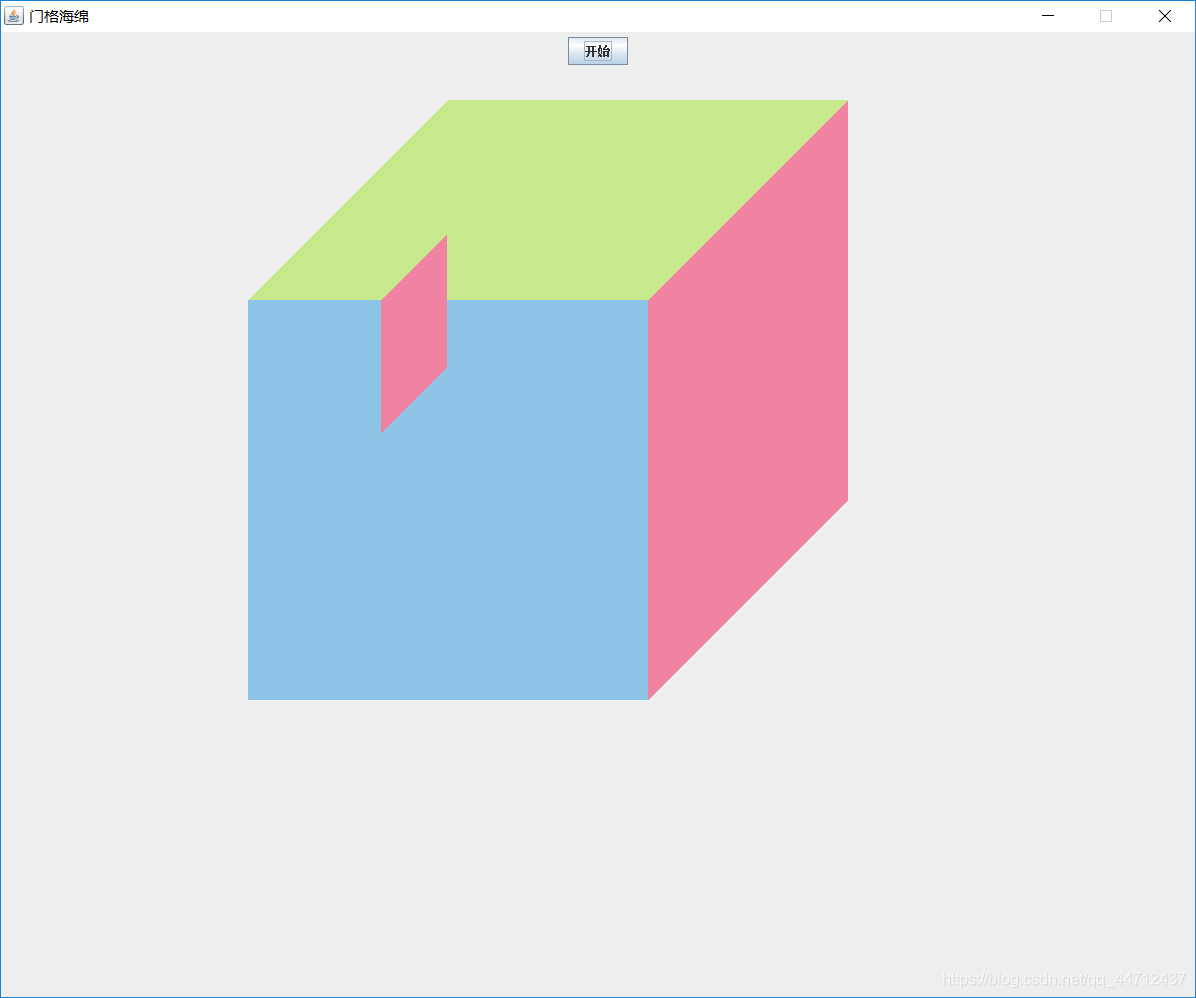
在这里插入图片描述
接着画1号的小立方体时，1号立方体的上面（0123）填充的颜色就会把0号立方体的粉色那面覆盖一部分，前面（0354）又会覆盖粉色的一部分，加起来就完全覆盖了，就会如下面效果：
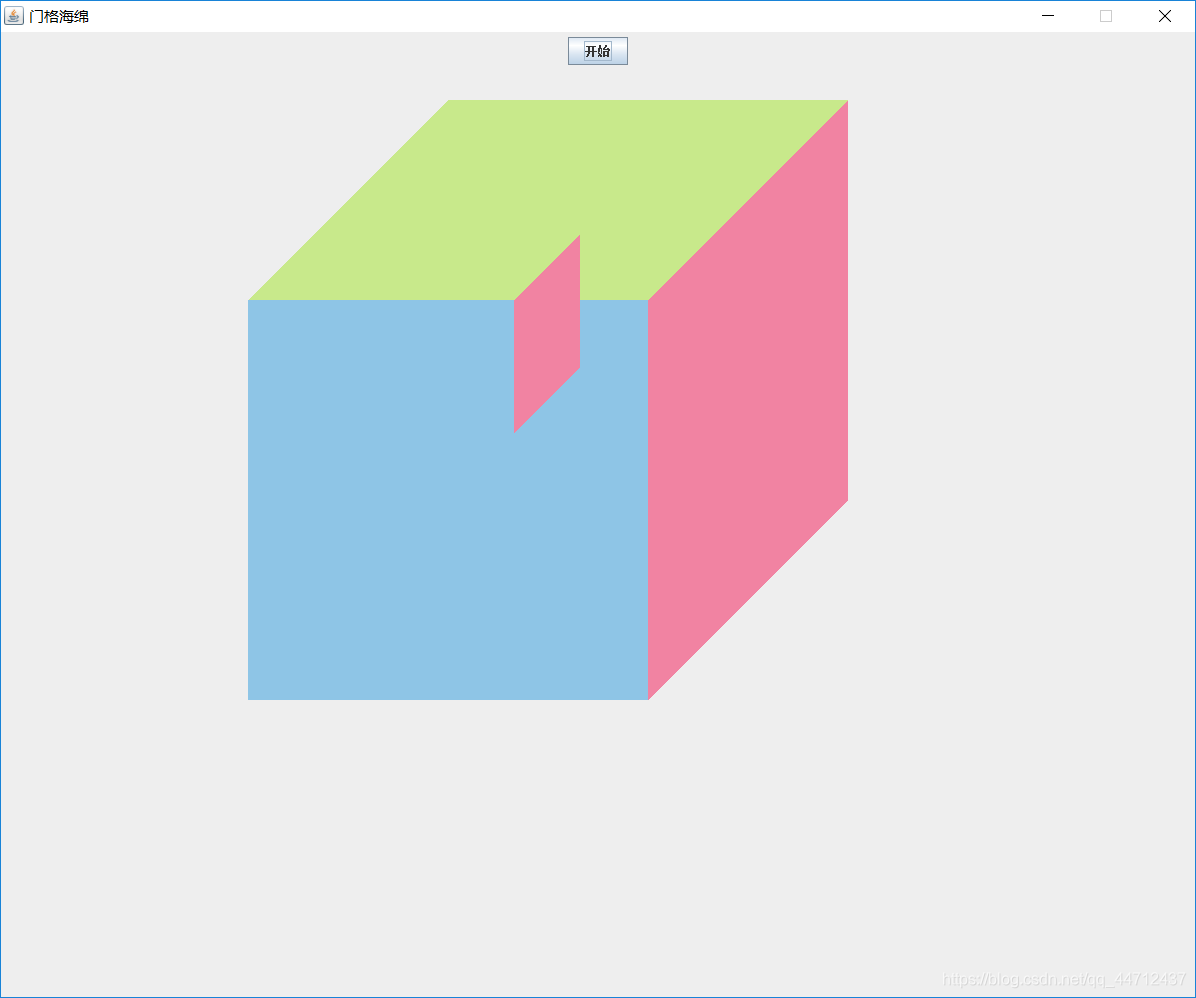
在这里插入图片描述
2号同理，但到了3号：
在这里插入图片描述
所以在使用递归画小立方体的时候，你要清楚哪个小立方体要在哪个小立方体后面画才能让颜色有序覆盖。
正确代码如下：

//第三层Point pp3[] = new Point[8];pp3[0] = new Point(p.x,p.y+2*d/3);pp3[1] = new Point(p.x+d/3,p.y+2*d/3);pp3[2] = new Point(p.x+2*d/3,p.y+2*d/3);pp3[3] = new Point(p.x+2*d/3+dx/3,p.y-dy/3+2*d/3);pp3[4] = new Point(p.x+2*d/3+dx*2/3,p.y-dy*2/3+2*d/3);pp3[5] = new Point(p.x+d/3+dx*2/3,p.y-dy*2/3+2*d/3);pp3[6] = new Point(p.x+dx*2/3,p.y-dy*2/3+2*d/3);pp3[7] = new Point(p.x+dx/3,p.y-dy/3+2*d/3);drawMenGe(pp3[6],d/3,dx/3,dy/3,count);drawMenGe(pp3[5],d/3,dx/3,dy/3,count);drawMenGe(pp3[4],d/3,dx/3,dy/3,count);drawMenGe(pp3[3],d/3,dx/3,dy/3,count);drawMenGe(pp3[7],d/3,dx/3,dy/3,count);drawMenGe(pp3[0],d/3,dx/3,dy/3,count);drawMenGe(pp3[1],d/3,dx/3,dy/3,count);drawMenGe(pp3[2],d/3,dx/3,dy/3,count);//第二层Point pp2[] = new Point[4];pp2[0] = new Point(p.x,p.y+d/3);pp2[1] = new Point(p.x+2*d/3,p.y+d/3);pp2[2] = new Point(p.x+2*d/3+dx*2/3,p.y-dy*2/3+d/3);pp2[3] = new Point(p.x+dx*2/3,p.y-dy*2/3+d/3);drawMenGe(pp2[0],d/3,dx/3,dy/3,count);drawMenGe(pp2[2],d/3,dx/3,dy/3,count);drawMenGe(pp2[1],d/3,dx/3,dy/3,count);drawMenGe(pp2[3],d/3,dx/3,dy/3,count);//第一层Point pp1[] = new Point[8];pp1[0] = new Point(p.x,p.y);pp1[1] = new Point(p.x+d/3,p.y);pp1[2] = new Point(p.x+2*d/3,p.y);pp1[3] = new Point(p.x+2*d/3+dx/3,p.y-dy/3);pp1[4] = new Point(p.x+2*d/3+dx*2/3,p.y-dy*2/3);pp1[5] = new Point(p.x+d/3+dx*2/3,p.y-dy*2/3);pp1[6] = new Point(p.x+dx*2/3,p.y-dy*2/3);pp1[7] = new Point(p.x+dx/3,p.y-dy/3);drawMenGe(pp1[6],d/3,dx/3,dy/3,count);drawMenGe(pp1[5],d/3,dx/3,dy/3,count);drawMenGe(pp1[4],d/3,dx/3,dy/3,count);drawMenGe(pp1[3],d/3,dx/3,dy/3,count);drawMenGe(pp1[7],d/3,dx/3,dy/3,count);drawMenGe(pp1[0],d/3,dx/3,dy/3,count);drawMenGe(pp1[1],d/3,dx/3,dy/3,count);drawMenGe(pp1[2],d/3,dx/3,dy/3,count);

正确效果为：
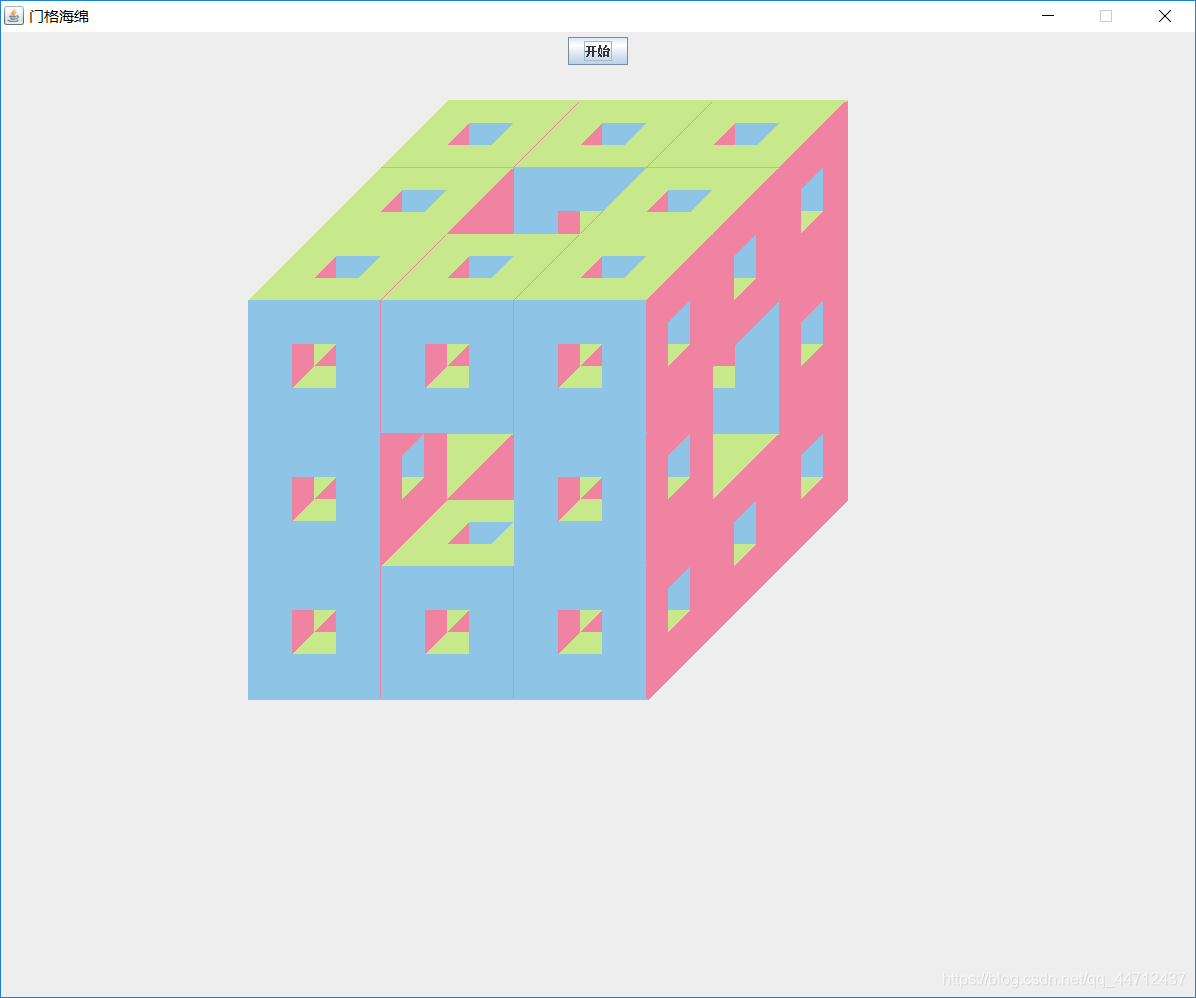
在这里插入图片描述
记录下心得：当时画这个鬼东西，画了两天，一开始不知道是画图顺序的问题，纠结了好久一直找不到问题，后来没有直接填充颜色，用画线的方式检查了一下，发现图形的立体结构没有出现错误，然后就开始一层一层，一个一个立方体的慢慢找错误，终于发现是颜色的覆盖出了问题。思路并不难，但是因为代码多了，容易忽略某些细节，还有各个代码之间的调试，出现bug找出来也很难，非要一步一步，从小细节慢慢找，慢慢检查。以后碰到更复杂的实现过程时，就更要注意。


http://chatgpt.dhexx.cn/article/CR1GEEQl.shtml

相关文章

复杂分形，简单规则：门格海绵世界探秘

复杂分形，简单规则：门格海绵世界探秘

连绵的山川、飘浮的云朵、岩石的断裂口、布朗粒子运动的轨迹、树冠、花菜、大脑皮层……这些部分与整体以某种方式相似的形体&#xff0c;可以说&#xff0c;就是“分形”的要义了&#xff0c;也恰恰是这些“不规则的”、“分散的”、“支离破碎的”物体又重新让我们认识了自然…
阅读更多...
JQData | 高校版使用教程，30秒安装完成，自带Python环境

JQData | 高校版使用教程，30秒安装完成，自带Python环境

本地量化金融数据JQData&#xff0c;是聚宽数据团队专门为金融机构、学术团体和量化研究者们提供的本地量化金融数据服务。自有版权&#xff0c;支持国内多家头部券商实盘交易。历经15万量化研究者与数百家机构使用验证。 JQData目前已支持国内30 高校&#xff0c;本次更新&…
阅读更多...
JQData + matplotlib 实现回测日志的交易细节可视化 量化数据接口

JQData + matplotlib 实现回测日志的交易细节可视化 量化数据接口

原文&#xff1a;https://zhuanlan.zhihu.com/p/49051899 前言&#xff1a; 做量化交易的朋友都知道回测的重要性&#xff0c;回测结果是衡量一个量化交易策略是否靠谱的重要依据。回测平台会按历史行情数据模拟成交&#xff0c;并将回测结果汇总成报告。 在很多时候&#xf…
阅读更多...
Note: Python学习笔记 -- Anaconda install jqdata

Note: Python学习笔记 -- Anaconda install jqdata

运行代码下列代码&#xff0c;提示错误 没有安装 jqdata。打开Anaconda Prompt 输入 pip install jqdata 提示cannot find command git然后百度了半天&#xff0c;有人说 pip install git 出错可以使用 conda install git 但是依然出错。最后去官网下载了Git:https://git-scm.…
阅读更多...
jq使用教程01_最贴心教程，安装JQData全靠这篇指南

jq使用教程01_最贴心教程，安装JQData全靠这篇指南

Hi, 各位亲爱的小伙伴们&#xff01; 近来听说有部分小伙伴在安装JQData时遇到了点小麻烦&#xff0c;导致最后没有安装成功&#xff0c;为了帮助小伙伴们快速成功安装JQData&#xff0c;小编今天来为大家排一下“雷”&#xff0c;希望能帮到你们哟 (&#xff65;ω&#xff6…
阅读更多...
事件驱动的选股小工具（JQData）

事件驱动的选股小工具（JQData）

昨天发改委下发了《关于积极推进风电、光伏发电无补贴平价上网有关工作的通知》&#xff0c;也不知道对股市是利空还是利多。连夜做了一个搜索公司经营范围的小工具,看看那些股票受到影响。 以后还可以增加筛选条件&#xff0c;比如财务指标&#xff0c;剔除ST股票&#xff0c;…
阅读更多...
股票python量化交易008-JoinQuant中JQData的使用

股票python量化交易008-JoinQuant中JQData的使用

查阅JoinQuant中JQData的使用文档python代码实现导入JQData，并认证用户身份。认证完毕显示“auth success”后即可使用 from jqdatasdk import *; auth(ID,Password);#ID是申请时所填写的手机号；Password为聚宽官网登录密码 # 查询jqdata的调用次数情况 surplus_count = g…
阅读更多...
jqdata pyechart： 用grid双图实现k线带图成交 — by QUANTAXIS

jqdata pyechart： 用grid双图实现k线带图成交 — by QUANTAXIS

from jqdatasdk import * from pyecharts import Kline,Bar,Grid 首先我们先应JQDATA 的活动演示一下如何调用pyecharts 画图 auth(acc,password) dataget_price(000001.XSHE) auth success先打印下 data 我们可以看到 jqdata返回的格式是 一个单index的Dataframe data.he…
阅读更多...
Quant | JQData使用API简单梳理（二）

Quant | JQData使用API简单梳理（二）

聚宽平台实际上提供了两种查询数据的方法，第一种是线上在聚宽平台可以使用的API：jqdata，另外一种则是本地的接口：JQData，是的，你没有看错，只是大小写的不同，搞得一开始我以为完全是同一种。jqdata可以线上通过import jqdata来引入数据接口，本地的JQData则是通过import…
阅读更多...
jqdata(data是什么文件格式)

jqdata(data是什么文件格式)

期货交易中bar和tick是什么意思 Bar 的概念 在一定时间段内的时间序列就构成了一根 K 线(日本蜡烛图)&#xff0c;单根 K 线被称为 Bar。 如果是一分钟内的 Tick 序列&#xff0c;即构成一根分钟 K 线&#xff0c;又称分钟 Bar; 如果是一天内的分钟序列&#xff0c;即构成一根日…
阅读更多...
JQData | 量化界最好用的本地量化金融数据（free free~）

JQData | 量化界最好用的本地量化金融数据（free free~）

什么是本地量化金融数据 - JQData &#xff1f; 使用JQData本地量化金融数据服务&#xff0c;可快速查看、计算或接入金融数据信息&#xff0c;解决本地、web、自研金融终端调用数据的需求。支持python多版本及多操作系统。为财经类企业、金融机构、学术研究机构和量化爱好者们…
阅读更多...
获取股票数据【使用JQData查询行情数据、财务指标、估值指标】

获取股票数据【使用JQData查询行情数据、财务指标、估值指标】

了解股票&#xff1a; 在上一次量化小科普【什么是量化&#xff1f;常用的股票量化指标、如何搭建量化交易系统】对于量化的概念有了一个基本认识&#xff0c;其中量化的主体在这门课程的学习中是“股票”&#xff0c;而当别人问你&#xff1a;“什么是股票&#xff1f;”&…
阅读更多...
JQData安装的问题（本地调用的量化金融数据接口-免费）

JQData安装的问题（本地调用的量化金融数据接口-免费）

JQData简介（1）JQData是聚宽数据团队专门为有志于从事量化投资的金融机构、研究人员以及个人量化爱好者提供的本地量化金融数据。用户只需在本地Python环境下安装JQData数据包，输入三行代码，即可调用由聚宽数据团队专业生产的全套量化金融数据，让你轻松告别平台限制，灵活安…
阅读更多...
JQData安装(转)

JQData安装(转)

首先&#xff0c;JQData是基于python的一个数据包&#xff0c;所以安装JQData的第一步是安装Python &#xff08;没有接触过python或者python基础不好的小伙伴&#xff0c;可以关注聚宽量化课堂的python讲堂进行python学习&#xff09;。 对于python安装包的选择&#xff0c;…
阅读更多...
JQData安装的问题（只解决安装的问题）

JQData安装的问题（只解决安装的问题）

1. JQData简介 &#xff08;1&#xff09;JQData是聚宽数据团队专门为有志于从事量化投资的金融机构、研究人员以及个人量化爱好者提供的本地量化金融数据。用户只需在本地Python环境下安装JQData数据包&#xff0c;输入三行代码&#xff0c;即可调用由聚宽数据团队专业生产的…
阅读更多...
JQData-本地调用的量化金融数据接口（免费）

JQData-本地调用的量化金融数据接口（免费）

什么是聚宽数据-JQData？ 使用JQData金融数据服务，可快速查看、计算或接入金融数据信息，解决本地、web、自研金融终端调用数据的需求。支持python多版本及多操作系统。为财经类企业、金融机构、学术研究机构和量化爱好者们提供一站式财经信息服务及数据解决方案。 提供哪些…
阅读更多...
JQData安装 | 最贴心教程，安装JQData全靠这篇指南

JQData安装 | 最贴心教程，安装JQData全靠这篇指南

转自 JQData安装 | 最贴心教程&#xff0c;安装JQData全靠这篇指南 Hi, 各位亲爱的小伙伴们&#xff01; 首先&#xff0c;感谢聚宽小编 JQData01 给我开放了更多的数据访问资源 近来听说有部分小伙伴在安装JQData时遇到了点小麻烦&#xff0c;导致最后没有安装成功&#xff0c…
阅读更多...
如何理解敏捷开发

如何理解敏捷开发

目录 什么是敏捷开发 2.0 常用的 4 种开发模式 瀑布式开发 迭代式开发 螺旋式开发 敏捷软件开发 4 种开发模式总结 什么是 DevOps 精益管理的7个原则 DevOps的开发流程 提交 编译 单元测试 部署到测试环境中 预生产测试 部署到生产环境 敏捷开发 2.0 解决的问…
阅读更多...
什么是敏捷？什么是敏捷开发？

什么是敏捷？什么是敏捷开发？

什么是敏捷&#xff1f; 显示敏捷相互馈送的各个方面的关系图&#xff0c;例如协作、开发和自动化版本控制和部署。 敏捷是一个术语&#xff0c;描述软件开发方法&#xff0c;强调增量交付、团队协作、持续规划和持续学习。 敏捷术语于 2001 年在敏捷宣言中创造。 宣言旨在制定…
阅读更多...
瀑布式开发与敏捷开发的区别是什么

瀑布式开发与敏捷开发的区别是什么

摘要&#xff1a;瀑布模型式是最典型的预见性的方法&#xff0c;严格遵循预先计划的需求、分析、设计、编码、测试的步骤顺序进行。敏捷开发以用户的需求进化为核心&#xff0c;采用迭代、循序渐进的方法进行软件开发。我们将在文章中详细说明两者各自的适合场景。 详细解答&am…
阅读更多...
推荐文章

Copyright @ 2022~2023