研究混沌运动,少不了对分形理论的探讨。分形:通常被定义为“一个粗糙或零碎的几何形状,可以分成数个部分,且每一部分都(至少近似地)是整体缩小后的形状”,即具有自相似的性质。
本篇将从一维过度到三维介绍分形图案的产生,一维类比康托尔集直线三等分的生成,此处比较简单我们不过多讨论,我们重点分析如何通过使用Java语言,实现Sierpinski和Menger sponge分形图案的过程(多图)。
谢尔宾斯基(Sierpinski)三角形
谢尔宾斯基三角形和它本身的一部分完全相似,它是自相似集的经典例子。
构造特点
- 取一个三角形边框(常用等边三角形)
- 沿三边中点的连线,将它分成四个小三角形
- 去掉中间的那一个小三角形
- 对其余三个小三角形都重复1~3的操作
代码实现
UI界面鼠标监听器获取鼠标点击处的坐标,再由此坐标和等腰三角的边长关系,得到三角形其余两点坐标:
int x = (int)e.getX();
int y = (int)e.getY();
int length = 120;//设定三角形边长为2*length
int x2 = x+length;//以下为坐标变换
int x3 = x-length;
int y2 = (int)(y-length*Math.sqrt(3));
int y3 = (int)(y-length*Math.sqrt(3));
int count =6;//迭代次数初始值方法一:
此方法是绘制Sierpinski三角形的典型思路,与构造特点思路对应。
public void triangle_1(int x1,int y1,int x2,int y2,int x3,int y3,int count){//将三角形三顶点坐标存入数组中int m[]={x1,x2,x3};int n[]={y1,y2,y3};//绘制三角形边框g.drawPolygon(m, n, 3);//迭代次数减1,再判断count--;if(count>0){//计算三边中点坐标int x4=(x1+x2)/2;int x5=(x1+x3)/2;int x6=(x2+x3)/2;int y4=(y1+y2)/2;int y5=(y1+y3)/2;int y6=(y2+y3)/2;//迭代到不包括最中间的其余三个小三角形中triangle_1(x1,y1,x4,y4,x5,y5,count);triangle_1(x2,y2,x4,y4,x6,y6,count);triangle_1(x3,y3,x5,y5,x6,y6,count);}}
绘制结果(1)

此结果是迭代6次的效果,三顶点变换方向不同,效果会有区别,但大同小异。
方法二:
与方法一的思路略有不同,我们不排除中间的三角形,而是以它为主,先绘制最中间的实心三角形,再对三边的三个不同方向作迭代,变化过程中只改变三角形边长大小为之前的1/2,并朝此方向作平移,重复上述过程。
public void triangle_2(int length,int x1,int y1,int x2,int y2,int x3,int y3,int l){/*此处代码作用是将三角形三顶点坐标转换,并保存至数组中由于与上述重复,不再赘述*///判断断边长大小决定是否继续递归if(length>4){g.setColor(new Color(length,l/4,length+l/4));g.fillPolygon(m, n, 3);length = length/2;//边长递减一半l = (int) (2*length*Math.sqrt(3)); //小三角形每次变化所要平移的距离System.out.println("X坐标:"+m[0]+"-"+m[1]+"-"+m[2]+" Y坐标:"+n[0]+"-"+n[1]+"-"+n[2]+" 边长="+2*length);g.setColor(new Color(l/4,l/4+length,l/4));g.fillPolygon(m, n, 3);//迭代到不包括最中间的其余三个小三角形中triangle_2(length,x1,y1,x2,y2,x3,y3,l);triangle_2(length,x1+2*length,y1+l,x2+2*length,y2+l,x3+2*length,y3+l,l);triangle_2(length,x1-2*length,y1+l,x2-2*length,y2+l,x3-2*length,y3+l,l);}}绘制结果(2)

迭代过程中对三角形的填充的颜色做了变化,如果变换背景颜色,与最后迭代时小三角形颜色相近,会产生更好的效果:

同理,Sierpinski矩形地毯的绘制思路与Sierpinski三角形完全一致,不再赘述,只是我们可以多些变化,比如添加倒角效果如下:

可能渐变效果并不好,此处只是分享一种变化的思路,Sierpinski的部分我们就介绍到这里。
门格海绵(Menger sponge)
它是康托尔集和谢尔宾斯基地毯在三维空间的推广
构造特点
- 画出一个立方体
- 将它等分三层(底层,中层,顶层)即等分27个完全相同的小立方体
- 掏空每一面中央的小立方体,包括最内层的小立方体
- 对剩余的20个小立方体都重复1~3的操作,并渐变填充每个小立方体的三面,使其更有立体感
过程如图:


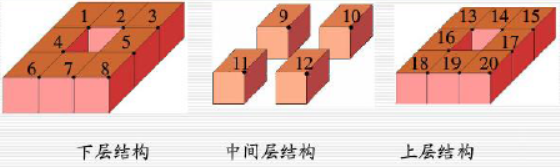
代码实现
网上随已有现成源码,但所做封装较多,普遍篇幅较长,本人整理如下的代码量可以缩减到一半以下,可读性大大提高。对比另一种方法:单靠不断叠加for循环的实现过程,此方法避免了代码尾段落全是 } 的尴尬,修改也更便捷,只需设定初始迭代值即可,逻辑更清晰易懂。
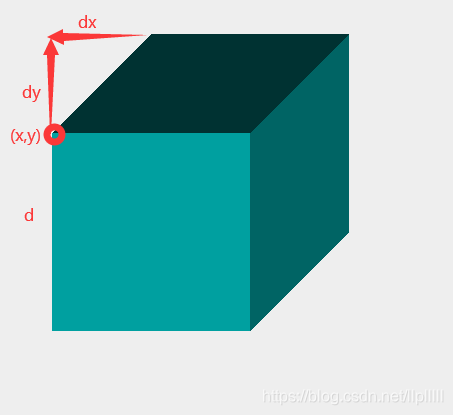
int x = (int)e.getX();int y = (int)e.getY();int count =6;int d=486,dx=243,dy=243; //正方体边长、右、上侧透视深度由于绘制立方体不会用到被遮挡的顶角,所以只需记录7个顶角坐标。其中P0点是我们认定的小方块起始绘制的首地址。
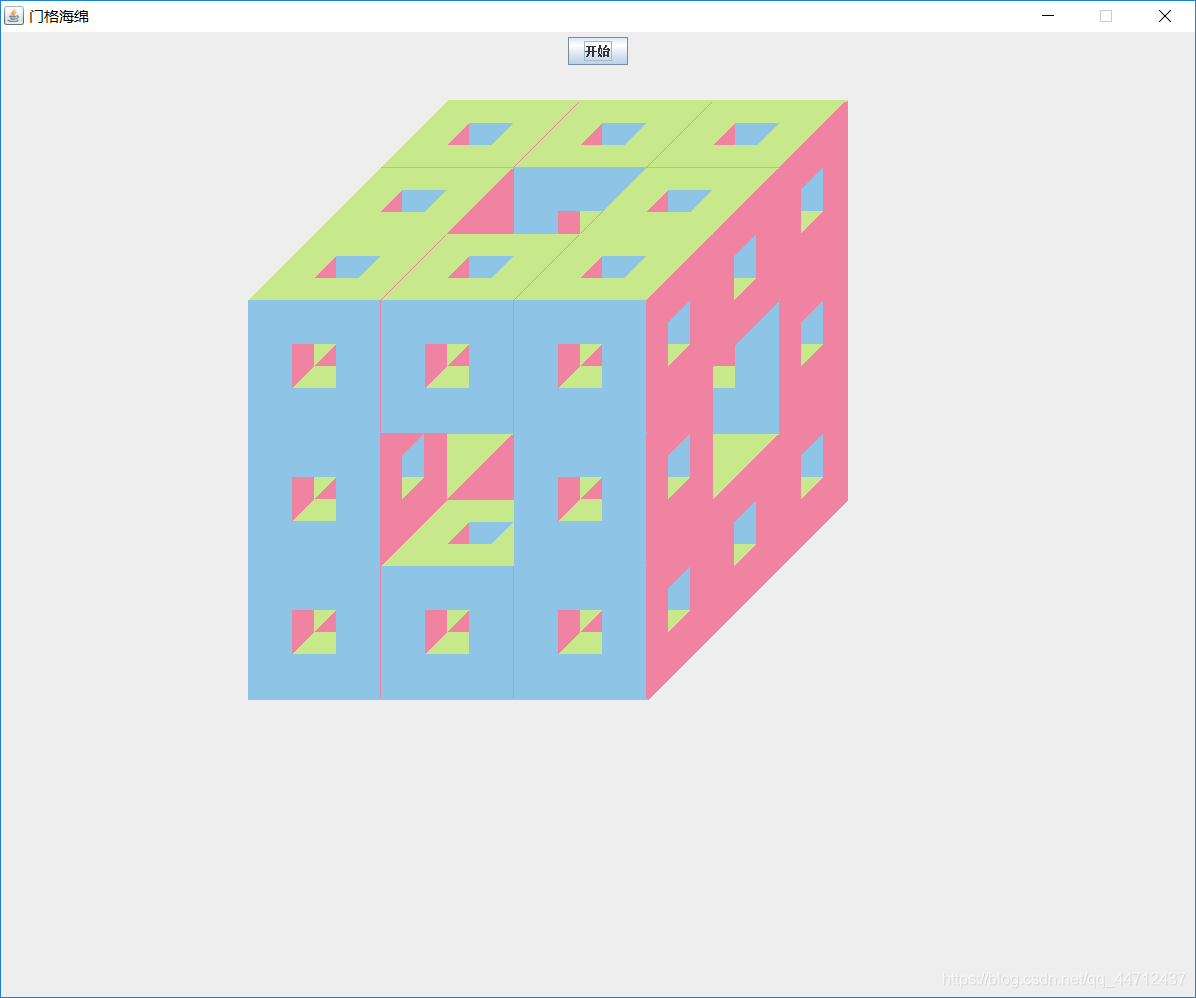
public void Menger_Sponge(int x,int y,int d,int dx,int dy,int count){//记录单个方块7个顶角的坐标Point p0 = new Point(x,y);Point p1 = new Point(p0.x+d,p0.y);Point p2 = new Point(p1.x,p1.y+d);Point p3 = new Point(p2.x-d,p2.y);Point p4 = new Point(p0.x+dx,p0.y-dy);Point p5 = new Point(p1.x+dx,p1.y-dy);Point p6 = new Point(p2.x+dx,p2.y-dy);count--; //递归次数减1if(count>=0){//递归到底层各小方块的首地址Menger_Sponge(p0.x+2*dx/3,p0.y-2*dy/3+2*d/3,d/3,dx/3,dy/3,count);Menger_Sponge(p0.x+2*dx/3+d/3,p0.y-2*dy/3+2*d/3,d/3,dx/3,dy/3,count);Menger_Sponge(p0.x+2*dx/3+2*d/3,p0.y-2*dy/3+2*d/3,d/3,dx/3,dy/3,count);Menger_Sponge(p0.x+dx/3,p0.y-dy/3+2*d/3,d/3,dx/3,dy/3,count);Menger_Sponge(p0.x+dx/3+2*d/3,p0.y-dy/3+2*d/3,d/3,dx/3,dy/3,count);Menger_Sponge(p0.x,p0.y+2*d/3,d/3,dx/3,dy/3,count);Menger_Sponge(p0.x+d/3,p0.y+2*d/3,d/3,dx/3,dy/3,count);Menger_Sponge(p0.x+2*d/3,p0.y+2*d/3,d/3,dx/3,dy/3,count);//递归到中层各小方块的首地址Menger_Sponge(p0.x+2*dx/3,p0.y-2*dy/3+d/3,d/3,dx/3,dy/3,count);Menger_Sponge(p0.x+2*dx/3+2*d/3,p0.y-2*dy/3+d/3,d/3,dx/3,dy/3,count);Menger_Sponge(p0.x,p0.y+d/3,d/3,dx/3,dy/3,count);Menger_Sponge(p0.x+2*d/3,p0.y+d/3,d/3,dx/3,dy/3,count);//递归到顶层各小方块的首地址Menger_Sponge(p0.x+2*dx/3,p0.y-2*dy/3,d/3,dx/3,dy/3,count);Menger_Sponge(p0.x+2*dx/3+d/3,p0.y-2*dy/3,d/3,dx/3,dy/3,count);Menger_Sponge(p0.x+2*dx/3+2*d/3,p0.y-2*dy/3,d/3,dx/3,dy/3,count);Menger_Sponge(p0.x+dx/3,p0.y-dy/3,d/3,dx/3,dy/3,count);Menger_Sponge(p0.x+dx/3+2*d/3,p0.y-dy/3,d/3,dx/3,dy/3,count);Menger_Sponge(p0.x,p0.y,d/3,dx/3,dy/3,count);Menger_Sponge(p0.x+d/3,p0.y,d/3,dx/3,dy/3,count);Menger_Sponge(p0.x+2*d/3,p0.y,d/3,dx/3,dy/3,count);}else{//填充正面矩形Polygon poly1 = new Polygon();poly1.addPoint(p0.x, p0.y);poly1.addPoint(p1.x, p1.y);poly1.addPoint(p2.x, p2.y);poly1.addPoint(p3.x, p3.y);g.setColor(new Color(150,0,0));g.fillPolygon(poly1);//填充右面矩形Polygon poly2 = new Polygon();poly2.addPoint(p1.x, p1.y);poly2.addPoint(p2.x, p2.y);poly2.addPoint(p6.x, p6.y);poly2.addPoint(p5.x, p5.y);g.setColor(new Color(200,0,0));g.fillPolygon(poly2);//填充上面矩形Polygon poly3 = new Polygon();poly3.addPoint(p0.x, p0.y);poly3.addPoint(p1.x, p1.y);poly3.addPoint(p5.x, p5.y);poly3.addPoint(p4.x, p4.y);g.setColor(new Color(100,0,0));g.fillPolygon(poly3);}}绘制结果

这是迭代3次产生的结果,需要注意的是,三等分边长可能会出现浮点数,故建议按照3的倍数来设定初始值,以防各小方块分离的情况。
结尾
不论一维的cantor集,还是二维的Sierpinski地毯,又或者三维的Menger sponge绘制,迭代的思路无非都遵循了分形图案的特点:每个局部的形状都是整体图案缩小的效果,局部再分形也同样符合。
所以包括L-树,科赫雪花等分形图案的绘制我们也能如法炮制。
问题
门格海绵的绘制中,时间复杂度大,随着迭代次数增加,耗时明显变多有没有更好的方法可以解决这种问题呢?
例如:立方体的8个顶点我们只需要保存7个,立方体的6个面我们只需要绘制出3个,迭代过程中的小立方体有些是被遮挡不需要绘制的,如果我们能有更好的算法,一次性画出迭代的门格海绵,那么这个问题可以得到很好的解决。