创意画板延伸内容

article/2025/1/6 19:26:18

在完成了创意画板的基础功能实现后，我们就可以通过画板来绘制一些有趣的图形了

1.平面山脉图

 

效果图如上

山脉图是由一个个山峰构成的，所以先绘制一个山峰

而山峰的绘制算法是：先确定两个点A B，然后获取A B的中间点P，其中P的x值为A Bx轴向上的中点，P点的y值是以A By中值为基础，在（-k，k）范围内随机取值。算出P点后，对AP BP 进行如上的相通算法，不过k值要减小，迭代下去。在所有的点计算完成后，将点连线就获得了一个山脉曲线。

具体代码实现如下，其中N为迭代次数，K为初始缩小比例

//山峰public void shanfen(int x1,int y1,int x2,int y2,int N,Graphics gr,double k){
​int y = (y1 + y2)/2;if(N>1){int px,py;int ran = (int)((Math.random()*800-400)*k);px = (x1 +x2)/2;py = ran + y;k*=0.5;//等比缩小shanfen(x1,y1,px,py,N-1,gr,k);shanfen(px,py,x2,y2,N-1,gr,k);
​
​}else {gr.drawLine(x1,y1,x2,y2);}
​}

这样，你就获得了一张这样的山脉曲线

 

现在我们可以将颜色填充进去

注意到山脉曲线的绘制实际上是一条条线段构成的，所以我们可以在绘制每一条线段之后给线段下方填充颜色

这里要用到Polygon类中的填充方法

Polygon py = new Polygon();//创建Polygon类的对象
py.addPoint(x1,y1);//依次添加点，注意要依次添加，具体可以自己尝试
py.addPoint(x2,y2);
py.addPoint(x2,2000);//y值可以自己定
py.addPoint(x1,2000);
int r = (int)Math.random()*256;//这里我取随机颜色
int g = (int)Math.random()*256;
int b = (int)Math.random()*256;
gr.setColor(new Color(r,g,b,128));//128是指透明度
gr.fillPolygon(py);//填充方法
gr.setColor(new Color(0,0,0,255));//复原透明度

 

 

这样，我们就获得了一张这样的图形

然后山脉就是多绘制几次，我这里绘制了五次，就有了最初的效果了。

2.谢宾斯基地毯

效果图如下

 

 

谢宾斯基地毯的绘制原理是给定两个点A B,将以AB为对角点的矩形均分为九宫格，将九宫格中间部分涂黑，然后对剩下的八个宫格进行相同操作

具体代码如下，其中N为迭代次数

//谢宾斯基地毯
public void xiefu(int x1,int y1,int x2,int y2,int N,Graphics gr){
​if(N > 1){gr.fillRect(x1 + (x2 - x1)/3,y1 + (y2 - y1)/3,(x2 - x1)/3,(y2 - y1)/3);//画笔的填充方法
​xiefu(x1,y1,x1 + (x2 - x1)/3,y1 + (y2 - y1)/3,N - 1,gr);//分别对八个宫格进行迭代
​xiefu(x1 + (x2 - x1)/3,y1,x1 + 2*(x2 - x1)/3,y1 + (y2 - y1)/3,N - 1,gr);
​xiefu(x1 + 2*(x2 - x1)/3,y1,x2,y1 + (y2 - y1)/3,N - 1,gr);
​xiefu(x1,y1 + (y2 - y1)/3,x1 + (x2 - x1)/3,y1 + 2*(y2 - y1)/3,N - 1,gr);
​xiefu(x1 + 2*(x2 - x1)/3,y1 + (y2 - y1)/3,x2,y1 + 2*(y2 - y1)/3,N - 1,gr);
​xiefu(x1,y1 + 2*(y2 - y1)/3,x1 + (x2 - x1)/3,y2,N - 1,gr);
​xiefu(x1 + (x2 - x1)/3,y1 + 2*(y2 - y1)/3,x1 + 2*(x2 - x1)/3,y2,N - 1,gr);
​xiefu(x1 + 2*(x2 - x1)/3,y1 + 2*(y2 - y1)/3,x2,y2,N - 1,gr);
​}
​
}

其核心编程思想是跟山脉的绘制一样的，都是利用的迭代算法能存储数据的能力。

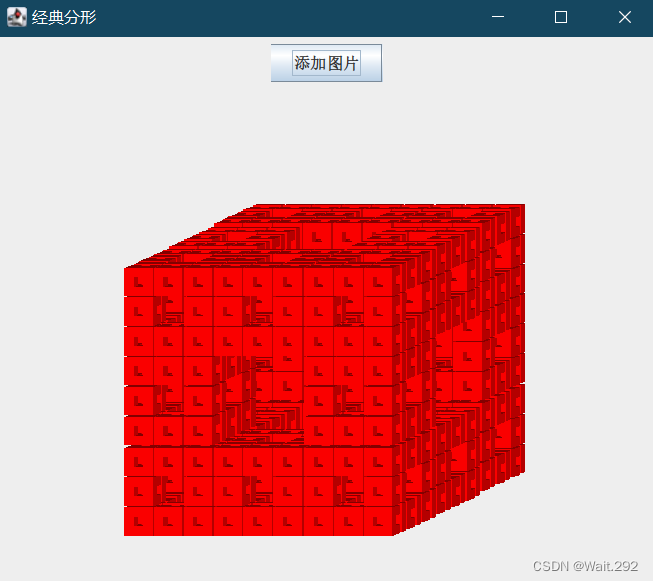
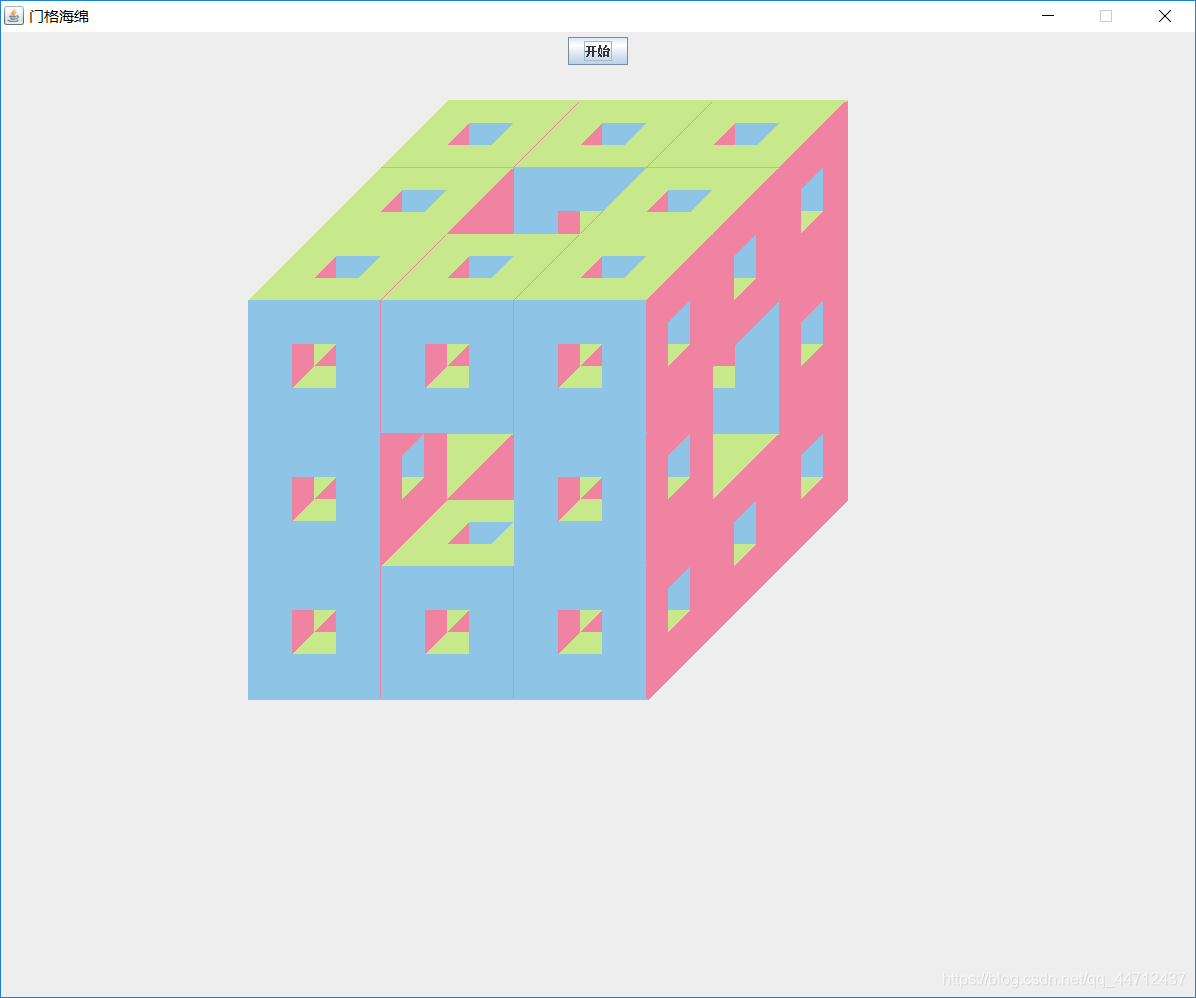
3.门格海绵

效果图如下

 

 

门格海绵是谢宾斯基地毯的立体版，想要绘制门格海绵，就需要先绘制出立体的正方体（矩形也行，这里我选择了正方体）

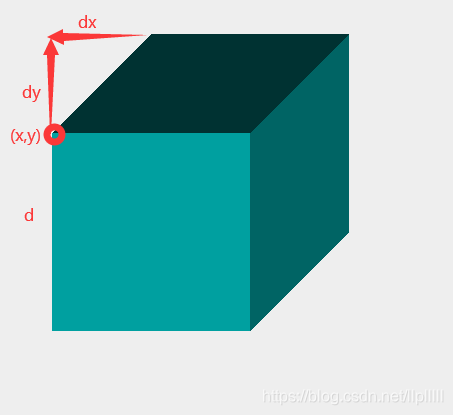
绘制立体正方体就是绘制我们看见的立体正方体的线，然后将不同的面填充不同的颜色以达到区分的效果

//绘制正方体
public void drawCube(int x1,int y1,int x2,int y2,Graphics gr){
​int dx = (x2-x1)/2;int dy = (y2-y1)/2;
​
​//绘线gr.drawLine(x1,y1,x2,y1);gr.drawLine(x2,y1,x2,y2);gr.drawLine(x2,y2,x1,y2);gr.drawLine(x1,y2,x1,y1);gr.drawLine(x1,y1,x1+dx,y1-dy);gr.drawLine(x2,y1,x2+dx,y1-dy);gr.drawLine(x2,y2,x2+dx,y2-dy);gr.drawLine(x1+dx,y1-dy,x2+dx,y1-dy);gr.drawLine(x2+dx,y1-dy,x2+dx,y2-dy);
​//填充颜色Polygon py = new Polygon();py.addPoint(x1,y1);py.addPoint(x2,y1);py.addPoint(x2,y2);py.addPoint(x1,y2);gr.setColor(new Color(200,100,100));//三个面填充不同的颜色，以便区分gr.fillPolygon(py);
​Polygon py1 = new Polygon();py1.addPoint(x1,y1);py1.addPoint(x2,y1);py1.addPoint(x2+dx,y1-dy);py1.addPoint(x1+dx,y1-dy);gr.setColor(new Color(100,200,100));gr.fillPolygon(py1);
​Polygon py2 = new Polygon();py2.addPoint(x2,y1);py2.addPoint(x2,y2);py2.addPoint(x2+dx,y2-dy);py2.addPoint(x2+dx,y1-dy);gr.setColor(new Color(100,100,200));gr.fillPolygon(py2);
​
}

这样，我们就可以获得一个看起来是立体的正方体

 

 

下一步就是进行迭代，与谢宾斯基地毯的思路一样，对正方体操作，然后再对需要重复操作的地方进行迭代，用N控制迭代次数

门格海绵是将正方体（长方体）均分成27份(以谢宾斯基地毯的划分形式),然后将每个面的中间正方体和中心正方体掏去。再对每个小正方体进行相同操作

效果是这样子的

 

具体代码如下： 

public void drawSponge(int x1,int y1,int x2,int y2,Graphics gr,int N){if(N > 1){int dx = (x2-x1)/2;int dy = (y2-y1)/2;
​//后面8个drawSponge(x1+2*dx/3,y1+2*(y2-y1)/3-2*dy/3,x1+(x2-x1)/3+2*dx/3,y2-2*dy/3,gr,N-1);drawSponge(x1+(x2-x1)/3+2*dx/3,y1+2*(y2-y1)/3-2*dy/3,x1+2*(x2-x1)/3+2*dx/3,y2-2*dy/3,gr,N-1);drawSponge(x1+2*dx/3+2*(x2-x1)/3,y1+2*(y2-y1)/3-2*dy/3,x2+2*dx/3,y2-2*dy/3,gr,N-1);
​drawSponge(x1+2*dx/3,y1+(y2-y1)/3-2*dy/3,x1+(x2-x1)/3+2*dx/3,y1+2*(y2-y1)/3-2*dy/3,gr,N-1);drawSponge(x1+2*(x2-x1)/3+2*dx/3,y1+(y2-y1)/3-2*dy/3,x2+2*dx/3,y1+2*(y2-y1)/3-2*dy/3,gr,N-1);
​drawSponge(x1+2*dx/3,y1-2*dy/3,x1+(x2-x1)/3+2*dx/3,y1+(y2-y1)/3-2*dy/3,gr,N-1);drawSponge(x1+(x2-x1)/3+2*dx/3,y1-2*dy/3,x1+2*(x2-x1)/3+2*dx/3,y1+(y2-y1)/3-2*dy/3,gr,N-1);drawSponge(x1+2*(x2-x1)/3+2*dx/3,y1-2*dy/3,x2+2*dx/3,y1+(y2-y1)/3-2*dy/3,gr,N-1);
​//中间四个drawSponge(x1+dx/3,y1+2*(y2-y1)/3-dy/3,x1+(x2-x1)/3+dx/3,y2-dy/3,gr,N-1);drawSponge(x1+dx/3+2*(x2-x1)/3,y1+2*(y2-y1)/3-dy/3,x2+dx/3,y2-dy/3,gr,N-1);drawSponge(x1+dx/3,y1-dy/3,x1+(x2-x1)/3+dx/3,y1+(y2-y1)/3-dy/3,gr,N-1);drawSponge(x1+dx/3+2*(x2-x1)/3,y1-dy/3,x2+dx/3,y1+(y2-y1)/3-dy/3,gr,N-1);
​//正面8个drawSponge(x1,y1+2*(y2-y1)/3,x1+(x2-x1)/3,y2,gr,N-1);drawSponge(x1+(x2-x1)/3,y1+2*(y2-y1)/3,x1+2*(x2-x1)/3,y2,gr,N-1);drawSponge(x1+2*(x2-x1)/3,y1+2*(y2-y1)/3,x2,y2,gr,N-1);
​drawSponge(x1,y1+(y2-y1)/3,x1+(x2-x1)/3,y1+2*(y2-y1)/3,gr,N-1);drawSponge(x1+2*(x2-x1)/3,y1+(y2-y1)/3,x2,y1+2*(y2-y1)/3,gr,N-1);
​drawSponge(x1,y1,x1+(x2-x1)/3,y1+(y2-y1)/3,gr,N-1);drawSponge(x1+(x2-x1)/3,y1,x1+2*(x2-x1)/3,y1+(y2-y1)/3,gr,N-1);drawSponge(x1+2*(x2-x1)/3,y1,x2,y1+(y2-y1)/3,gr,N-1);
​
​}else{drawCube(x1,y1,x2,y2,gr);
​}
}

注意，由于绘制次序的原因，后绘制的图形会覆盖先绘制的图形，所以绘制正方体的时候要先绘制大部分看不见的,就是后面的，在绘制前面的，先绘制下面的，再绘制上面的。

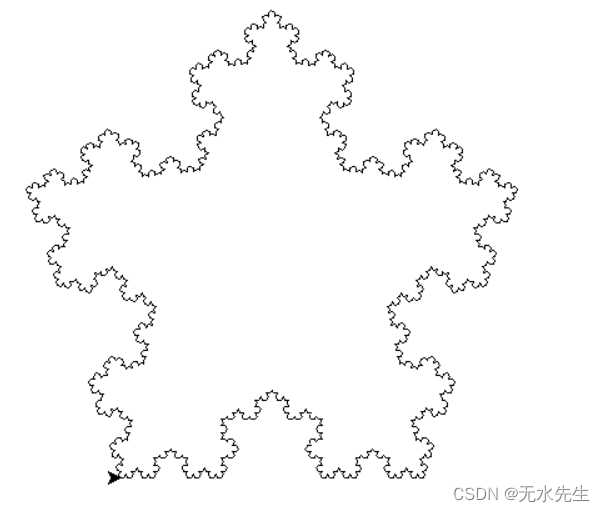
4.分形的绘制

IFS manual

 

 

 

以上的三个效果图是就根据我提供的网站中类似

 

这样的算法实现的

其中set1234的意思是，在你每次要算新的xy时随机等概率选取其中一组值进行计算，x0y0可以随机选取。

例如其中枫叶图形的绘制

//枫叶
public void drawMaple(double x,double y,Graphics gr){
​
​for (int i = 0; i < 7000000; i++) {int m = (int)(Math.random()*4);double xb = 0 ,yb = 0;if(m == 0){xb = 0.14*x + 0.01*y - 0.08;yb = 0.51*y - 1.31;gr.drawLine((int) (xb*100) + 700,(int) (yb*100) + 500,(int) (xb*100) + 700,(int) (yb*100) + 500);
​}if(m == 1){xb = 0.43*x + 0.52*y +1.49;yb = (-0.45)*x + 0.5*y - 0.75;gr.drawLine((int) (xb*100) + 700,(int) (yb*100) + 500,(int) (xb*100) + 700,(int) (yb*100) + 500);
​}if(m == 2){xb = 0.45*x - 0.49*y - 1.62;yb = 0.47*x + 0.47*y - 0.74;gr.drawLine((int) (xb*100) + 700,(int) (yb*100) + 500,(int) (xb*100) + 700,(int) (yb*100) + 500);
​
​}if(m == 3){xb = 0.49*x + 0.02;yb = 0.51*y + 1.62;gr.drawLine((int) (xb*100) + 700,(int) (yb*100) + 500,(int) (xb*100) + 700,(int) (yb*100) + 500);
​
​}x = xb;y = yb;}
​
}

注意绘制比例的缩放和移动

 

其中也有一些加概率的，就是每次要算新的xy时，按概率选取数据进行计算就行

5.立体山脉

效果图

 

立体山脉的原理与绘制山峰类似

选取ABC三点，对AB,AC,BC进行山峰算法计算，算出DEF三点，然后对三角形ADE,BDF,DEF,CEF进行相同算法计算

其代码实现如下

 public void liti(int x1,int y1,int x2,int y2,int x3,int y3,Graphics gr,int N,double k){
​if(N > 1){int pax,pay,pbx,pby,pcx,pcy;pax = (x1 + x2)/2;pbx = (x1 + x3)/2;pcx = (x2 + x3)/2;
​double ran = (Math.random()*300-150)*k;pay = (int) ((y1 + y2)/2 + ran);pby = (int) ((y1 + y3)/2 + ran);pcy = (int) ((y2 + y3)/2 + ran);
​k*=0.5;liti(x1,y1,pax,pay,pbx,pby,gr,N-1,k);liti(pax,pay,x2,y2,pcx,pcy,gr,N-1,k);liti(pbx,pby,pcx,pcy,x3,y3,gr,N-1,k);liti(pcx,pcy,pbx,pby,pax,pay,gr,N-1,k);}else {gr.drawLine(x1,y1,x2,y2);gr.drawLine(x1,y1,x3,y3);gr.drawLine(x2,y2,x3,y3);}
​}

但是如果按照这种方法进行计算就会由这种效果

 

显然，这样的效果不对

分析一下，在三角形ADE中和三角形DEF中计算DE的中间波动点应该为同一个点，但是上面的代码计算了两次，算出两个不同的点，所以就会有了上面图形的效果

解决方案：由于算中间波动点是根据两个点的坐标进行计算的，所以我没计算出一个中间波动点，就将这两个用来计算的点和中间的点的坐标存储起来，下次计算时遍历一遍，如果下次计算时用来计算的两个点在存储的数据中，则直接使用之前算出来的点，如果不在，则算出新的点，存储进去。

理一下思路：

新建三个集合，两个用来存储用来计算的两个点的y坐标，一个用来存储算出来的点的y坐标，集合相同的坐标存储一套数据（两个原始点和算出来的点），每次计算新点时都将两个用来计算的点遍历一遍集合，如果有，就用，没有，就用新算出来的点

具体实现代码如下

    ArrayList yalist = new ArrayList();ArrayList yblist = new ArrayList();//用来存储两个用来计算的点的y坐标ArrayList yclist = new ArrayList();//用来存储计算出来的点的y坐标public void liti(int x1,int y1,int x2,int y2,int x3,int y3,Graphics gr,int N,double k){
​if(N > 1){int pax,pay,pbx,pby,pcx,pcy;pax = (x1 + x2)/2;pbx = (x1 + x3)/2;pcx = (x2 + x3)/2;
​double ran = (Math.random()*300-150)*k;pay = (int) ((y1 + y2)/2 + ran);pby = (int) ((y1 + y3)/2 + ran);pcy = (int) ((y2 + y3)/2 + ran);for (int i = 0; i < yalist.size(); i++) {if(y2 == (Integer)yalist.get(i) && y1 == (Integer)yblist.get(i)||y1 == (Integer)yalist.get(i) && y2 == (Integer)yblist.get(i)){pay = (Integer) yclist.get(i);}}for (int i = 0; i < yalist.size(); i++) {if(y1 == (Integer)yalist.get(i) && y3 == (Integer)yblist.get(i)||y3 == (Integer)yalist.get(i) && y1 == (Integer)yblist.get(i)){pby = (Integer) yclist.get(i);}}for (int i = 0; i < yalist.size(); i++) {if(y2 == (Integer)yalist.get(i) && y3 == (Integer)yblist.get(i)||y3 == (Integer)yalist.get(i) && y2 == (Integer)yblist.get(i)){pcy = (Integer) yclist.get(i);}}
​yalist.add(y2);yblist.add(y1);yclist.add(pay);yalist.add(y1);yblist.add(y3);yclist.add(pby);yalist.add(y2);yblist.add(y3);yclist.add(pcy);
​k*=0.5;liti(x1,y1,pax,pay,pbx,pby,gr,N-1,k);liti(pax,pay,x2,y2,pcx,pcy,gr,N-1,k);liti(pbx,pby,pcx,pcy,x3,y3,gr,N-1,k);liti(pcx,pcy,pbx,pby,pax,pay,gr,N-1,k);}else {gr.drawLine(x1,y1,x2,y2);gr.drawLine(x1,y1,x3,y3);gr.drawLine(x2,y2,x3,y3);}
​}

http://chatgpt.dhexx.cn/article/YWAu4LBU.shtml

相关文章

Java第六课——画图板

Java第六课——画图板

Java第六课——画图板 这节课画一个画图板&#xff0c;可以画线画圆&#xff0c;还可以通过递归画出好看的图案如&#xff1a;谢尔宾斯基三角形&#xff0c;康托尔方形集&#xff0c;甚至立体图门格海绵。 首先创建一个窗体。定义一个类和一个方法。 public class Draw{publ…
阅读更多...
分形理论中的分维解析

分形理论中的分维解析

最近打算利用一段时间好好学习一下分形理论&#xff0c;也写一系列博客记录下自己的学习归纳情况。下面是这部分文章的目录&#xff1a; 一、分形理论的历史过程 二、分形理论的基础概念 三、分形理论的分维解析 四、分形理论的Hausdorff维数 五、分形理论的盒维数 六、分形理论…
阅读更多...
python绘制n阶科赫曲线线段_分形几何中科赫雪花的绘制

python绘制n阶科赫曲线线段_分形几何中科赫雪花的绘制

目录分形几何在自然界中广泛存在（康托尔集、谢尔滨斯基三角形、门格海绵、龙形曲线、科赫曲线...)，实际上分形几何是一种迭代的几何图形。本文主要讨论科赫曲线。 科赫曲线的绘制： import turtle def koch(size,n):#绘制科赫曲线含俩个参数，大小和阶数 if n == 0:#基线情…
阅读更多...
【计算几何】大自然的数学模型--分形几何

【计算几何】大自然的数学模型--分形几何

一、前言 分形几何是几何数学中的一个分支&#xff0c;也称大自然几何学&#xff0c;由著名数学家本华曼德勃罗&#xff08; 法语&#xff1a;BenoitB.Mandelbrot&#xff09;在 1975 年构思和发展出来的一种新的几何学。分形几何是对大自然中微观与宏观和谐统一之美的发现&…
阅读更多...
Java分形递归——门格海绵

Java分形递归——门格海绵

门格海绵的结构简单来说就是从一个正方体开始&#xff1b;再把正方体的每一个面分成9个正方形&#xff0c;这时就形成了由27个小正方体组成的一个大正方体&#xff1b;然后再把每一面的中间的正方体和最中心的正方体去掉&#xff0c;最终留下20个正方体。最后&#xff0c;把每一…
阅读更多...
门格海绵的实现

门格海绵的实现

实现效果&#xff1a; 源代码&#xff1a; package sponge;import java.awt.Color; import java.awt.Graphics; import java.awt.Graphics2D; import java.awt.Point; import java.awt.Polygon;import javax.swing.JFrame;public class Sponge_Main extends JFrame impleme…
阅读更多...
混沌与分形（一）：谢尔宾斯基三角形与门格海绵

混沌与分形（一）：谢尔宾斯基三角形与门格海绵

研究混沌运动&#xff0c;少不了对分形理论的探讨。分形&#xff1a;通常被定义为“一个粗糙或零碎的几何形状&#xff0c;可以分成数个部分&#xff0c;且每一部分都&#xff08;至少近似地&#xff09;是整体缩小后的形状”&#xff0c;即具有自相似的性质。 本篇将从一维过…
阅读更多...
分形之门格海绵

分形之门格海绵

门格海绵解决思路&#xff1a; 1. 迭代如何实现 2. 立方体该怎么画 3. 实现门格海绵代码 4. 画图板门格海绵代码 1. 迭代如何实现 为了实现从1图—>2图—>3图效果,我们就要想到用迭代去实现. 因为像3图这样的图形,是由若干个2图这样的基本图形组成的 那么,怎样实现…
阅读更多...
JAVA学习日志之门格海绵

JAVA学习日志之门格海绵

门格海绵的结构可以用以下方法形象化&#xff1a; 从一个正方体开始。&#xff08;第一个图像&#xff09; 把正方体的每一个面分成9个正方形。这将把正方体分成27个小正方体&#xff0c;像魔方一样。 把每一面的中间的正方体去掉&#xff0c;把最中心的正方体也去掉&#xff0…
阅读更多...
复杂分形，简单规则：门格海绵世界探秘

复杂分形，简单规则：门格海绵世界探秘

连绵的山川、飘浮的云朵、岩石的断裂口、布朗粒子运动的轨迹、树冠、花菜、大脑皮层……这些部分与整体以某种方式相似的形体&#xff0c;可以说&#xff0c;就是“分形”的要义了&#xff0c;也恰恰是这些“不规则的”、“分散的”、“支离破碎的”物体又重新让我们认识了自然…
阅读更多...
JQData | 高校版使用教程，30秒安装完成，自带Python环境

JQData | 高校版使用教程，30秒安装完成，自带Python环境

本地量化金融数据JQData&#xff0c;是聚宽数据团队专门为金融机构、学术团体和量化研究者们提供的本地量化金融数据服务。自有版权&#xff0c;支持国内多家头部券商实盘交易。历经15万量化研究者与数百家机构使用验证。 JQData目前已支持国内30 高校&#xff0c;本次更新&…
阅读更多...
JQData + matplotlib 实现回测日志的交易细节可视化 量化数据接口

JQData + matplotlib 实现回测日志的交易细节可视化 量化数据接口

原文&#xff1a;https://zhuanlan.zhihu.com/p/49051899 前言&#xff1a; 做量化交易的朋友都知道回测的重要性&#xff0c;回测结果是衡量一个量化交易策略是否靠谱的重要依据。回测平台会按历史行情数据模拟成交&#xff0c;并将回测结果汇总成报告。 在很多时候&#xf…
阅读更多...
Note: Python学习笔记 -- Anaconda install jqdata

Note: Python学习笔记 -- Anaconda install jqdata

运行代码下列代码&#xff0c;提示错误 没有安装 jqdata。打开Anaconda Prompt 输入 pip install jqdata 提示cannot find command git然后百度了半天&#xff0c;有人说 pip install git 出错可以使用 conda install git 但是依然出错。最后去官网下载了Git:https://git-scm.…
阅读更多...
jq使用教程01_最贴心教程，安装JQData全靠这篇指南

jq使用教程01_最贴心教程，安装JQData全靠这篇指南

Hi, 各位亲爱的小伙伴们&#xff01; 近来听说有部分小伙伴在安装JQData时遇到了点小麻烦&#xff0c;导致最后没有安装成功&#xff0c;为了帮助小伙伴们快速成功安装JQData&#xff0c;小编今天来为大家排一下“雷”&#xff0c;希望能帮到你们哟 (&#xff65;ω&#xff6…
阅读更多...
事件驱动的选股小工具（JQData）

事件驱动的选股小工具（JQData）

昨天发改委下发了《关于积极推进风电、光伏发电无补贴平价上网有关工作的通知》&#xff0c;也不知道对股市是利空还是利多。连夜做了一个搜索公司经营范围的小工具,看看那些股票受到影响。 以后还可以增加筛选条件&#xff0c;比如财务指标&#xff0c;剔除ST股票&#xff0c;…
阅读更多...
股票python量化交易008-JoinQuant中JQData的使用

股票python量化交易008-JoinQuant中JQData的使用

查阅JoinQuant中JQData的使用文档python代码实现导入JQData，并认证用户身份。认证完毕显示“auth success”后即可使用 from jqdatasdk import *; auth(ID,Password);#ID是申请时所填写的手机号；Password为聚宽官网登录密码 # 查询jqdata的调用次数情况 surplus_count = g…
阅读更多...
jqdata pyechart： 用grid双图实现k线带图成交 — by QUANTAXIS

jqdata pyechart： 用grid双图实现k线带图成交 — by QUANTAXIS

from jqdatasdk import * from pyecharts import Kline,Bar,Grid 首先我们先应JQDATA 的活动演示一下如何调用pyecharts 画图 auth(acc,password) dataget_price(000001.XSHE) auth success先打印下 data 我们可以看到 jqdata返回的格式是 一个单index的Dataframe data.he…
阅读更多...
Quant | JQData使用API简单梳理（二）

Quant | JQData使用API简单梳理（二）

聚宽平台实际上提供了两种查询数据的方法，第一种是线上在聚宽平台可以使用的API：jqdata，另外一种则是本地的接口：JQData，是的，你没有看错，只是大小写的不同，搞得一开始我以为完全是同一种。jqdata可以线上通过import jqdata来引入数据接口，本地的JQData则是通过import…
阅读更多...
jqdata(data是什么文件格式)

jqdata(data是什么文件格式)

期货交易中bar和tick是什么意思 Bar 的概念 在一定时间段内的时间序列就构成了一根 K 线(日本蜡烛图)&#xff0c;单根 K 线被称为 Bar。 如果是一分钟内的 Tick 序列&#xff0c;即构成一根分钟 K 线&#xff0c;又称分钟 Bar; 如果是一天内的分钟序列&#xff0c;即构成一根日…
阅读更多...
JQData | 量化界最好用的本地量化金融数据（free free~）

JQData | 量化界最好用的本地量化金融数据（free free~）

什么是本地量化金融数据 - JQData &#xff1f; 使用JQData本地量化金融数据服务&#xff0c;可快速查看、计算或接入金融数据信息&#xff0c;解决本地、web、自研金融终端调用数据的需求。支持python多版本及多操作系统。为财经类企业、金融机构、学术研究机构和量化爱好者们…
阅读更多...
推荐文章

Copyright @ 2022~2023