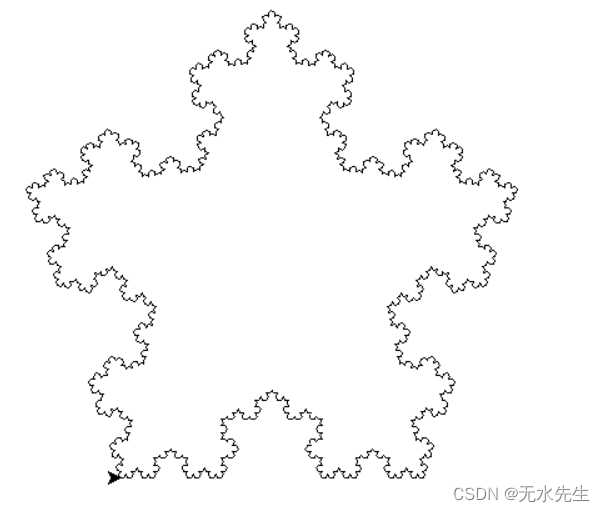
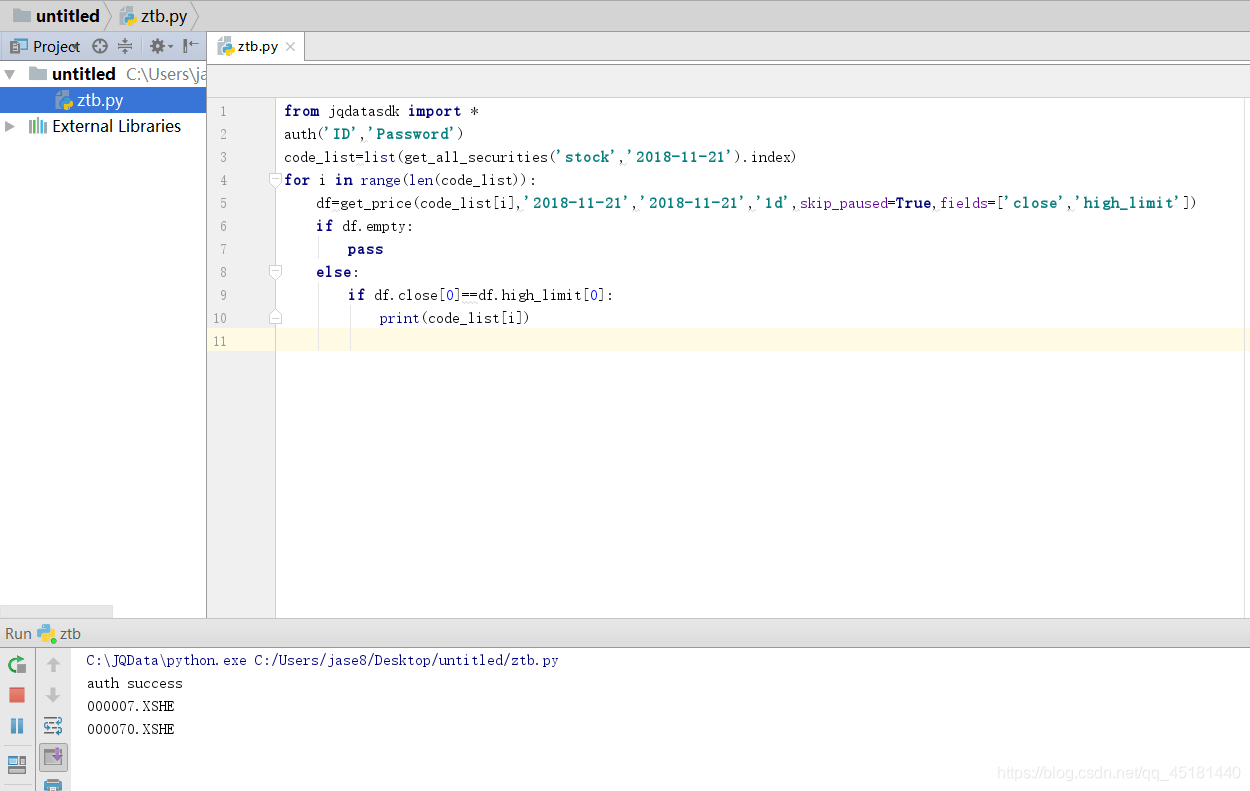
目录分形几何在自然界中广泛存在（康托尔集、谢尔滨斯基三角形、门格海绵、龙形曲线、科赫曲线...)，实际上分形几何是一种迭代的几何图形。本文主要讨论科赫曲线。

科赫曲线的绘制：

import turtle

def koch(size,n):#绘制科赫曲线含俩个参数，大小和阶数

if n == 0:#基线情况

turtle.fd(size)#0阶，即只有一条线段，直走

else:

for angle in [0,60,-120,60]:#当角度为0,60，120,60时

turtle.left(angle)#转动角度

koch(size/3,n-1)#在曲线1/3处递归调用科赫曲线

def main():

turtle.setup(800,400)

turtle.penup()

turtle.goto(-300,-50)

turtle.pendown()

turtle.pensize(2)

koch(600,3)#假设为三阶

turtle.hideturtle()

main()


## 基于科赫曲线绘制科赫雪花：

```python

import turtle

def koch