前言
本篇主要介绍函数和代码复用,以七段数码管绘制为例,介绍函数的定义和使用。以科赫雪花小包裹为例,介绍PyInstaller库的使用。
(从本篇开始,出现的一些库中函数介绍以及部分简单代码都将以图片形式呈现)
读完本篇,你将了解:
1.方法论
Python基本代码抽象即函数的使用方法
2.实践能力
学会编写带有函数并复用代码的程序
本篇将系统介绍:
1.函数的定义与使用
2.实例:七段数码管绘制
3.代码复用与函数递归
4.模块4:PyInstaller库的使用(将Python的源代码变成可执行文件,不用源代码即可执行,甚至在一些操作系统上,不需安装编译环境,实现程序的小包裹)
5.实例:科赫雪花小包裹(将分形几何、函数递归以及PyInstaller库结合在一起)
一、函数的定义与使用
1.函数的理解和定义
(1)介绍:函数是一段代码的表示,一段具有特定功能的、可重用的语句组
(2)函数是一种功能的抽象,一般函数表达特定功能
(3)两个作用︰降低编程难度和代码复用
(4)结构:
def <函数名>(<参数(0个或多个)>):
<函数体>
return<返回值>
(5)举例:计算n!

(6)几点注意
①函数定义时,所指定的参数是一种占位符
②函数定义后,如果不经过调用,不会被执行
③函数定义时,参数是输入、函数体是处理、结果是输出(IPO)
简单理解函数就是IPO的一种实现,也是一段完整代码的一种封装
2.函数的使用及调用过程
(1)调用
调用是运行函数代码的方式
①调用时要给出实际参数
②实际参数替换定义中的参数
③函数调用后得到返回值
(2)调用过程
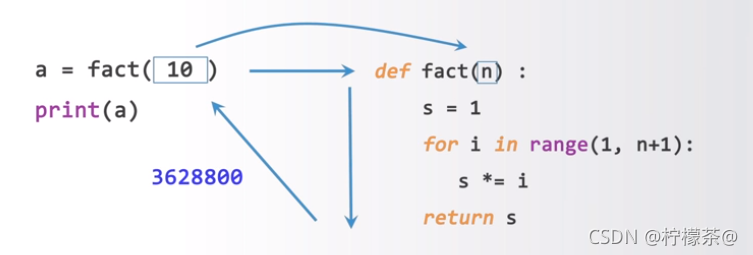
①左侧代码执行时,会去查找所定义的函数fact,
②将给定参数10赋给定义的函数中间的参数n,此时10就代替了定义函数中那个的n
③执行程序,产生具体的s值
④作为返回值返回给代码,赋值给变量a
3.函数的参数传递
(1)参数个数
①函数可以有参数,也可以没有,但必须保留括号
②结构:
def <函数名>():
<函数体>
return<返回值>
(2)可选参数传递
①调用参数时,某些变量不提供,只提供一些其他变量,函数定义时可以为某些参数指定默认值,构成可选参数
②结构:
def <函数名>(<非可选参数>, <可选参数>):
<函数体>
return<返回值>
③Python中要求在设定或定义函数的时候,所有可选参数必须放在非可选参数(必选参数)之后
④举例:

(3)可变参数传递
①函数定义时可以设计可变数量参数,既不确定参数总数量
②结构:(*b表示不确定参数)
def <函数名>(<参数>, *b):
<函数体>
return<返回值>
③举例:

(4)参数传递的两种方式
①函数调用时,参数可以按照位置或名称方式传递
②举例:

4.函数的返回值
(1)函数可以返回0个或多个结果
①return保留字用来传递返回值
②函数可以有返回值,也可以没有,可以有return,也可以没有
③return可以传递0个返回值,也可以传递任意多个返回值
(2)举例:

5.局部变量和全局变量
(1)定义:
①局部变量:函数体中使用的变量
②全局变量:函数外部整个程序使用的变量
(2)举例:

(3)规则1:局部变量和全局变量是不同变量
①局部变量是函数内部的占位符,与全局变量可能重名但不同
②函数运算结束后,局部变量被释放
③可以使用global保留字在函数内部使用全局变量
④举例:


(4)规则2:局部变量为组合数据(简单来说就是多个数组成的类型)类型且未创建,等同于全局变量
①举例:

append()函数:在列表中增加一个元素
运行结果:[‘F’,‘f’,‘C’]
②举例2:
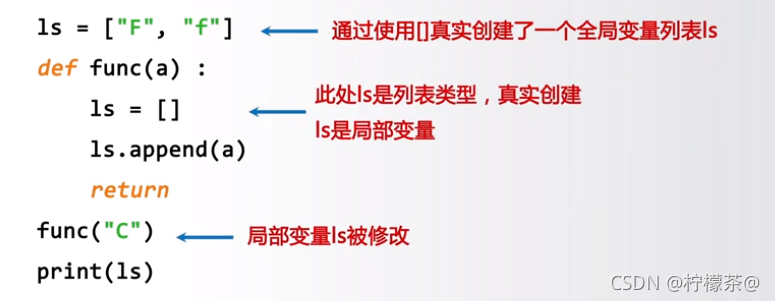
运行结果:[‘F’,‘f’]
6.lambda函数
(1)lambda函数返回函数名作为结果
①lambda函数是一种匿名函数,即没有名字的函数
②使用lambda保留字定义,函数名是返回结果
③lambda函数用于定义简单的、能够在一行内表示的函数
(2)结构:
<函数名> = lambda<参数>:<表达式>
(3)一种函数的紧凑表达形式
①返回的结果可以赋值为函数名字
②等价于def,return的函数
③区别:后边的内容只能使用表达式,不能使用函数体
(4)举例;
①

变量x,y。进行相加运算
②接收没有参数的函数

(5)谨慎使用lambda函数
①lambda函数主要用作一些特定函数或方法的参数
②lambda函数有一些固定使用方式,建议逐步掌握
③一般情况,建议使用def定义的普通函数
二、实例7:七段数码管绘制
1.问题分析
(1)七段数码管
①举例

它是由七段小的数码管构成的一个数字
②选择不同的数码管的量或者面。可以形成0到9、A到F不同的数字和字母组合
可通过这样的数码管,显示时间、字母。
③在交通灯路口、电子表上,有大量的七段数码管的效果
(2)需求及方法
①用程序绘制七段数码管
②turtle绘图体系
(3)给出效果

2.实例讲解
(1)基本思路
①步骤1∶绘制单个数字对应的数码管
②步骤2∶获得一串数字,绘制对应的数码管
③步骤3∶获得当前系统时间,绘制对应的数码管
(2)步骤1∶绘制单个数字数码管
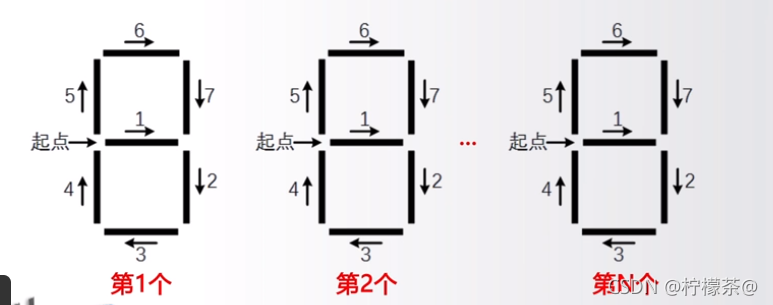
①七段数码管由7个基本线条组成
②七段数码管可以有固定顺序
③不同数字显示不同的线条
首先要能够绘制这七个基本线条
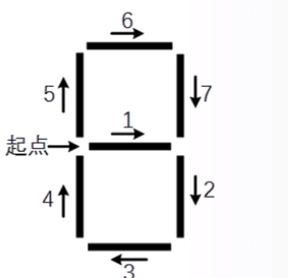
如果从左边的一个位置开始,可以将他们逐一编号,形成一个行动的序列,可以覆盖这七段线条
在七段线条中不同的线条是否被绘制,就能形成不同的绘制
④
import turtledef drawLine(draw): # 绘制单段数码管(一条线)turtle.pendown() if draw else turtle.penup() # draw是真值,海龟画笔落下进行真实绘制,如果不是,抬起画笔turtle.fd(40)turtle.right(90) # 行进40像素并转向90度def drawDigit(digit): # 根据数字绘制七段数码管drawLine(True) if digit in [2, 3, 4, 5, 6, 8, 9] else drawLine(False)drawLine(True) if digit in [0, 1, 3, 4, 5, 6, 7, 8, 9] else drawLine(False)drawLine(True) if digit in [0, 2, 3, 5, 6, 8, 9] else drawLine(False)drawLine(True) if digit in [0, 2, 6, 8] else drawLine(False)turtle.left(90) # 调用4次回到起点,转向90度回到前进方向,再进行3次右转drawLine(True) if digit in [0, 4, 5, 6, 8, 9] else drawLine(False)drawLine(True) if digit in [0, 2, 3, 5, 6, 7, 8, 9] else drawLine(False)drawLine(True) if digit in [0, 1, 2, 3, 4, 7, 8, 9] else drawLine(False)turtle.left(180)turtle.penup() # 为绘制后续数字确定位置turtle.fd(20) # 为绘制后续数字确定位置1)若不加判断,每一个线都会被绘制,结果为数字8
2)drawDigit函数:根据参数digit,来决定如何绘制对应的数字
3)参数digit:取值范围整数0-9
4)根据不同数字的显示位置进行判断,如果不是输入的数字,飞过去但不绘制
(3)步骤2∶获得一串数字,绘制多个数码管
在第一个结束时,将起点移动一个距离
def drawDate(date): # 获得要输出的数字for i in date:drawDigit(eval(i)) # 通过eval()函数将数字变为整数
(4)主函数
设定初始画布大小,当前画笔初始绘制所在的位置
运行效果

(5)优化:绘制漂亮的七段数码管(增加七段数码管之间线条间隔)
import turtledef drawGap(): # 绘制数码管间隔turtle.penup()turtle.fd(5)def drawLine(draw): # 绘制单段数码管(一条线)drawGap()turtle.penup() if not draw else turtle.pendown() # draw是真值,海龟画笔落下进行真实绘制,如果不是,抬起画笔turtle.fd(40)drawGap()turtle.right(90) # 行进40像素并转向90度drawGap函数:在绘制线之前和之后分别增加一些小的像素作为间隔
(6)步骤3∶获得当前系统时间,绘制对应的数码管
①使用time库获得系统当前时间
drawDate(time.strftime(’%Y-%m=%d+’, time.gmtime()))
获得一个内部的时间类型的当前时间,strftime对时间进行格式化
②增加年月日标记
③年月日颜色不同
④修改drawDate函数:
import turtle,timedef drawDate(date): # date为日期,格式为‘%Y-%m=%d+'turtle.pencolor("red")for i in date:if i == '-':turtle.write('年', font=("Arial", 18, "normal"))turtle.pencolor("green")turtle.fd(40)elif i == '=':turtle.write('月', font=("Arial", 18, "normal"))turtle.pencolor("blue")turtle.fd(40)elif i == '+':turtle.write('日', font=("Arial", 18, "normal"))else:drawDigit(eval(i))1)-、=、+分别对应年月日的汉字绘制
2)turtle.write函数绘制具体汉字,给定它的字体以及字号的大小
3)还可改变画笔颜色
⑤效果
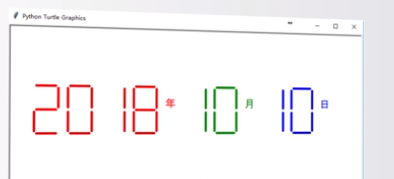
3.举一反三
(1)理解方法思维
①模块化思维:确定模块接口,封装功能
②规则化思维:抽象过程为规则,计算机自动执行
③化繁为简:将大功能变为小功能组合,分而治之
(2)应用问题的扩展
①绘制带小数点的七段数码管
②带刷新的时间倒计时效果
③绘制高级的数码管
三、代码复用与函数递归
1.代码复用与模块化设计
(1)把代码当成资源进行抽象
①代码资源化∶程序代码是一种用来表达计算的"资源"
②代码抽象化︰使用函数等方法对代码赋予更高级别的定义
③代码复用:同一份代码在需要时可以被重复使用
(2)代码复用
①两种主要形式:函数和对象,也可说二者是对代码进行抽象的不同级别
②函数:将代码命名,在代码层面建立了初步抽象
③对象︰属性和方法
a.b和a.b(),在函数之上再次组织进行抽象
(3)模块化设计:分而治之
①通过函数或对象封装将程序划分为模块及模块间的表达
②具体包括:主程序(看作模块与模块之间的关系)、子程序(看作模块)和子程序间关系
③分而治之(模块化设计的核心):一种分而治之、分层抽象、体系化的设计思想
(4)模块化设计两个基本概念
①紧耦合:两个部分之间交流很多,无法独立存在
②松耦合(有清晰简单的接口,可以独立存在):两个部分之间交流较少,可以独立存在
③注意:对函数的输入参数和返回值,越少越清晰,函数复用可能性越高
④模块内部紧耦合、模块之间松耦合
2.函数递归的理解
(1)递归的定义:函数定义中调用函数自身的方式(如n!)
(2)两个关键特征
①链条:计算过程存在递归链条
②基例(基础实例):存在一个或多个不需要再次递归的基例
(3)类似于数学归纳法
①证明当n取第一个值n。时命题成立
②假设当n,时命题成立,证明当n=nk,时命题也成立
③递归是数学归纳法思维的编程体现
3.函数递归的调用过程
(1)递归的实现
函数+分支语句
①递归本身是一个函数,需要函数定义方式描述
②函数内部,采用分支语句对输入参数进行判断
③基例和链条,分别编写对应代码
(2)举例:n!
def fact(n):if n == 0:return 1else:return n*fact(n-1)调用fact(5)
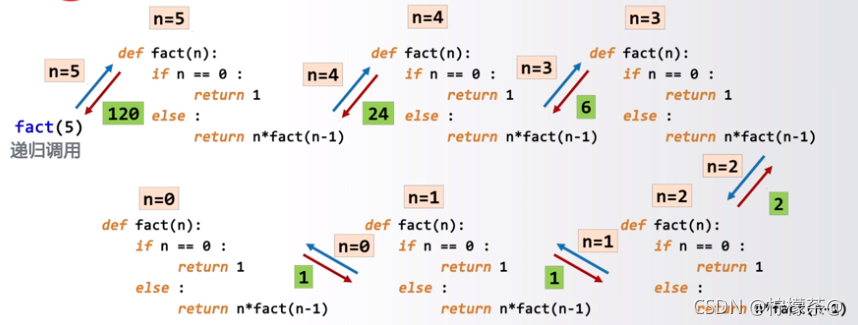
4.函数递归实例解析
(1)例一:字符串反转
将字符串s反转后输出
①可以不用递归,使用字符串的切片操作,s[ ::-1],从最开始到最后采用1的步长进行输出,而-1的步长就是指从后向前依次取出
②递归实现:区分递归链条和递归基例
def rvs(s):if s == "":return selse:return rvs(s[1:])+s[0](2)例二:斐波那契数列
天然给出两个基例:1和2
def f(n):if n==1 or n==2:return 1else:return f(n-1)+f(n-2)
(3)例三:汉诺塔问题
①问题分析:三根柱子,在一根柱子上从下往上按照大小顺序摞着圆盘。把圆盘从下面开始按大小顺序重新摆放在另一根柱子上。并且规定,在小圆盘上不能放大圆盘,在三根柱子之间一次只能移动一个圆盘。
②需要输出两个参数,搬运的次数和过程步骤
③抽象为三粮柱子分别是ABC,初始状态,所有圆盘放在柱子A上,那么经过一个中间柱子到达目标柱子C
④最佳解法是递归
count = 0def hanoi(n, src, dst, mid): # 圆盘数量,源柱子,目的柱子,过渡柱子global countif n == 1:print("{}:{}->{}".format(1, src, dst))count += 1else:hanoi(n - 1, src, mid, dst)print("{}:{}->{}".format(n, src, dst))count += 1hanoi(n - 1, mid, dst, src)四、模块4:PyInstaller库的使用
1.基本介绍
我们希望用可执行文件的方式来执行一段程序,而不是直接用源代码,我们需要将源程序首先编译,或者打包成一个直接可以执行的程序
(1)PyInstaller库概述:将.py源代码转换成无需源代码的可执行文件。不需按照解释器,也不需要对另一台计算机做环境配置
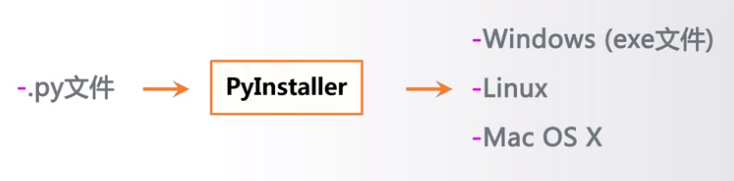
(2)PyInstaller库是第三方库
①第三方库:使用前需要额外安装
②安装第三方库需要使用pip工具
(3)PyInstaller库的安装
①打开Windows环境下的cmd命令行
②在命令行下执行命令pip install,后面加上我们希望安装的库的名称
(cmd命令行) pip install pyinstaller
③程序开始运行,pip指令在安装第三方库的时候,从互联网上自动下载安装包,安装之后会提示successfully installed
2.使用说明
(1)简单的使用
(cmd命令行)pyinstaller -F <文件名.py>
执行后打开目录,会看到目录中生成了额外的三个目录

①其中的build和pycache可以将它安全的删除掉
②而在dist的且录中你将会看到一个与原文件同名的exe文件,这个文件就是打包之后生成的文件
③双击即可执行
(2)常用参数
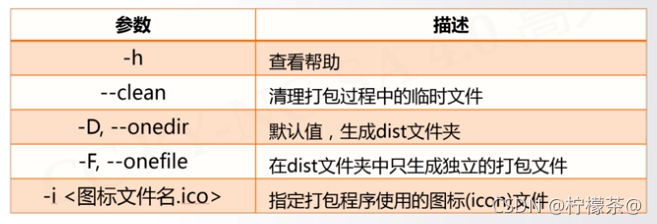
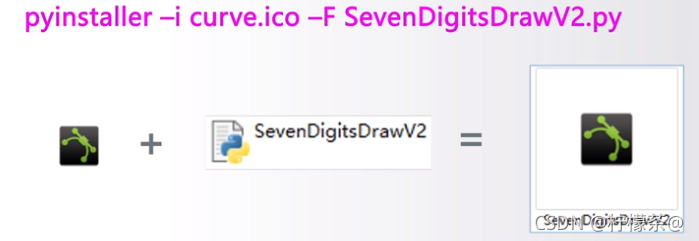
(3)举例:对一个源代码文件(七段数码管)关联一个图标,并且进行打包
五、实例8:科赫雪花小包裹
1.问题分析
(1)分形几何
①分形几何是一种迭代的几何图形,广泛存在于自然界中
②简单理解为,一个东西的整体与它的局部有很相似的特点
③其中一个特殊的曲线叫科赫曲线
(2)科赫曲线(也叫雪花曲线)
①雪花的边缘跟雪花的整体颜色和整体结构之间也存在着一定的相似性
②这种相似性可以表达为科赫曲线的一种数学描述
③科赫曲线是一种用于分形的曲线
(3)科赫雪花绘制
①首先拿出一条直线,取其中三分之一长度等分
②对于中间的1/3去掉,之后增加额外的两条线
③这样在一条长度为s的直线中,形成一个角度为60度的突起
④得到一个变种的曲线形式
一条直线到这样一种曲线的变换叫一次科赫曲线的转换
⑤每个短直线可再进行一次这样的操作

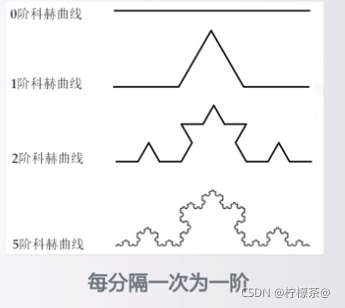
用同一个操作对其中的曲线或直线进行不断迭代,构成了科赫曲线的实现过程
2.实例讲解
(1)科赫曲线的绘制(n阶)
使用递归和海龟作图体系
# KochDrawV1
import turtledef koch(size, n): # 科赫曲线的绘制函数,两个参数:最开始绘制的每个直线的长度size,n阶if n == 0:turtle.fd(size)else:for angle in [0, 60, -120, 60]: # 最开始先确定一个角度turtle.left(angle) # 角度为0的时候,让整个海龟指向要绘制的方向koch(size/3, n-1)def main():turtle.setup(800, 400)turtle.penup()turtle.goto(-300, -50)turtle.pendown()turtle.pensize(2)koch(600, 3)turtle.hideturtle()(2)科赫曲线过渡到科赫雪花
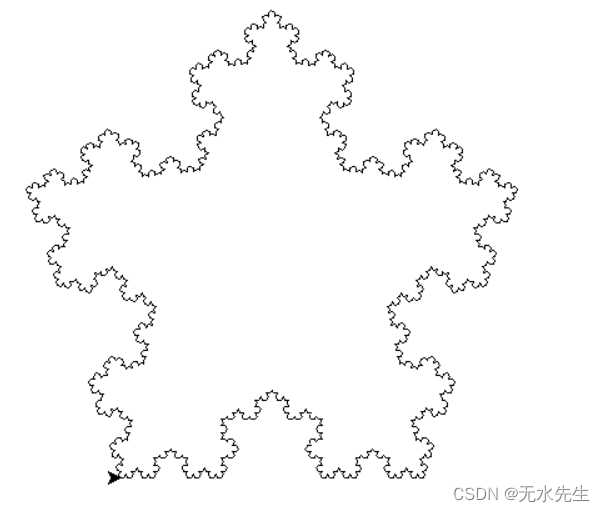
import turtledef koch(size, n): # 科赫曲线的绘制函数,两个参数:最开始绘制的每个直线的长度size,n阶if n == 0:turtle.fd(size)else:for angle in [0, 60, -120, 60]: # 最开始先确定一个角度turtle.left(angle) # 角度为0的时候,让整个海龟指向要绘制的方向koch(size/3, n-1)def main():turtle.setup(600, 600)turtle.penup()turtle.goto(-200, 100)turtle.pendown()turtle.pensize(2)level = 3 # 3阶科赫雪花,阶数koch(400, level)turtle.right(120)koch(400, level)turtle.right(120)koch(400, level)turtle.hideturtle()三条曲线首尾相接
(3)运行效果
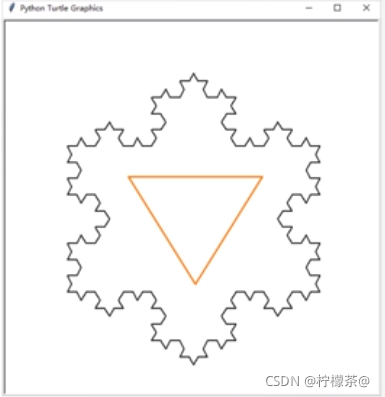
(4)打包
pyinstaller -i curve.ico -F KochDrawV2.py
3.举一反三
(1)绘制条件的扩展
①修改分形几何绘制阶数
②修改科赫曲线的基本定义及旋转角度
③修改绘制科赫雪花的基础框架图形
(2)多种分析几何
①·康托尔集、谢尔宾斯基三角形、门格海绵.….
②龙形曲线、空间填充曲线、科赫曲线…
③函数递归的深入应用.
总结
经过本篇的学习,可以大致掌握运用控制函数和代码复用去实现一些问题的实现,大家可以尝试不同的函数和代码复用去拓展更多的高级用法,进行多种分析几何的绘制,顺便回顾海龟绘图体系的使用。
注:代码非原创
下篇将介绍组合数据类型。