一、前言

        分形几何是几何数学中的一个分支，也称大自然几何学，由著名数学家本华曼德勃罗（ 法语：BenoitB.Mandelbrot）在 1975 年构思和发展出来的一种新的几何学。分形几何是对大自然中微观与宏观和谐统一之美的发现，并且揭示的部分只是冰山之一角，相信在人类认知的进步下，会开出一朵接一朵的美丽花朵。

        美国杰出的物理学家（ 两弹元勋 、现代广义相对论之父）、物理学思想家、物理学教育家惠勒（ Wheeler ）断言： “ 可以相信，明天谁不熟悉分形，谁就不能被认为是科学上的文化人。”可以看出分形强大的影响力，当然个人也比较喜欢分形，因为利用分形可以画出很多美丽的图形，利用分形我们可以描绘出 树叶的纹路、画出完整的一棵树、形状酷似病毒的图形，混沌 ( chaos )、孤立子( solitons )和分形 ( fractals )是非线性科学 ( nonlinear  science ) 中三个最重要的概念。

二、什么是分形

        分形（英语：fractal，源自拉丁语：frāctus，有“零碎”、“破裂”之意），又称碎形、残形，通常被定义为：

        “一个零碎的几何形状，可以分成数个部分，且每一部分都（至少近似地）是整体缩小后的形状”[2]，即具有自相似的性质。

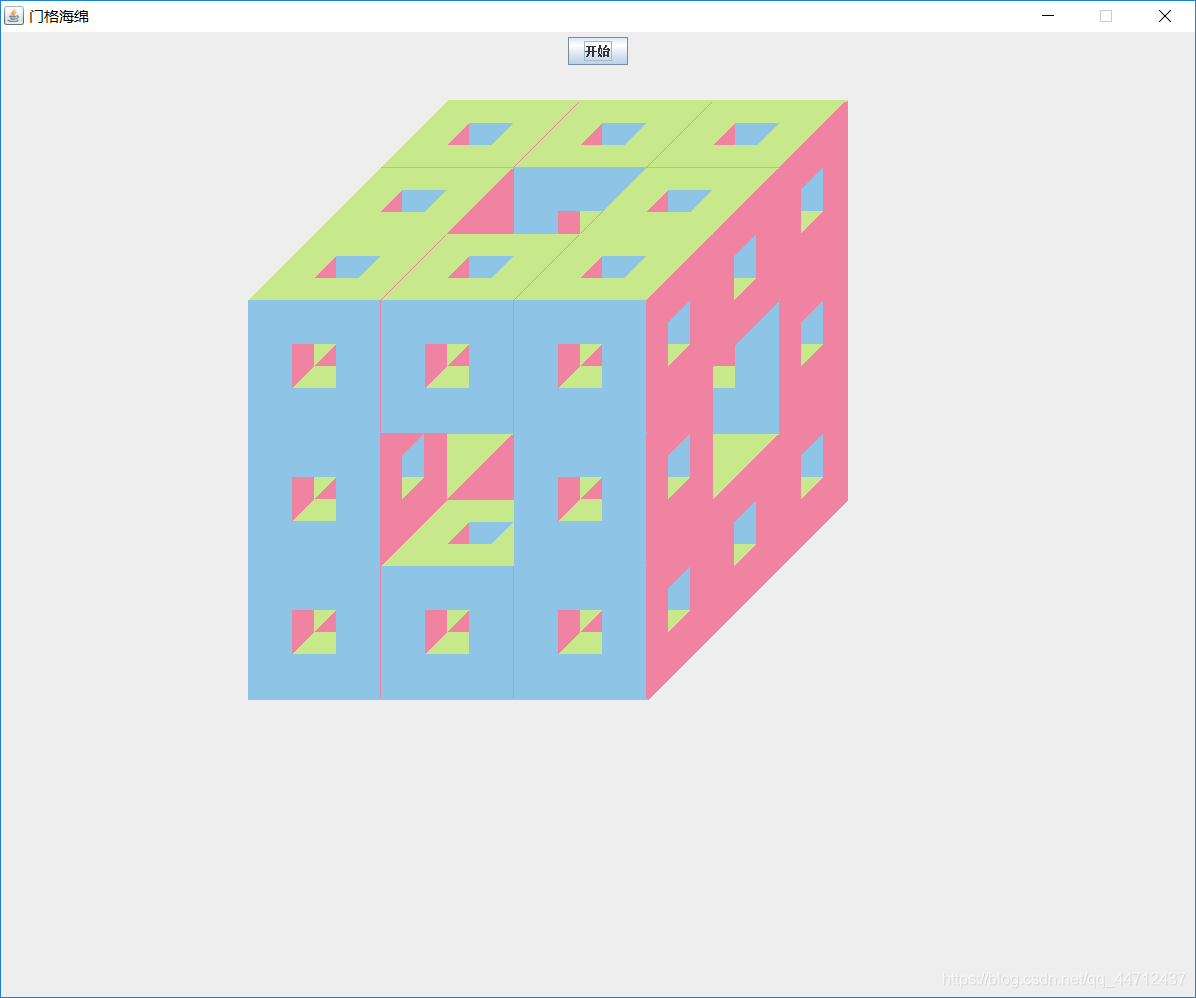
        分形在数学中是一种抽象的物体，用于描述自然界中存在的事物。人工分形通常在放大后能展现出相似的形状[3]。 分形也被称为扩展对称或展开对称。如果在每次放大后，形状的重复是完全相同的，这被称为自相似。自相似的一个例子是门格海绵[图1]。 分形在不同的缩放级别上可以是近似相似的。曼德博集合的【图2】放大图像中显示了这种模式[2][5][6][7]。 分形也包有图像的细节重复自身的意味。

三、关于自相似

        如果一个物体自我相似（Self-similarity），表示它和它本身的一部分完全或是几乎相似。若说一个曲线自我相似，即每部分的曲线有一小块和它相似。自然界中有很多东西有自我相似性质，例如海岸线。

3.1 谢尔宾斯基地毯（Sierpinski carpet、波兰语：Dywan Sierpińskiego）

        由波兰数学家瓦茨瓦夫·谢尔宾斯基（Wacław Sierpiński）于1916年提出的一种分形，是自相似集的一种。它的豪斯多夫维是 log 8/log 3 ≈ 1.8928。门格海绵是它在三维空间中的推广。

        将一个实心正方形划分为3X3的9个小正方形，去掉中间的小正方形，再对余下的小正方形重复这一操作便能得到谢尔宾斯基地毯。

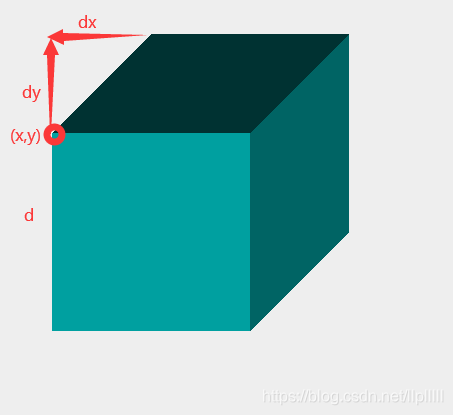
3.2 门格海绵说明

        门格海绵（英语：Menger sponge、英语：Menger universal curve）是分形的一种。它是一个通用曲线，因为它的拓扑维数为一，且任何其它曲线或图都与门格海绵的某个子集同胚。它有时称为门格-谢尔宾斯基海绵或谢尔宾斯基海绵。它是康托尔集和谢尔宾斯基地毯在三维空间的推广。它首先由奥地利数学家卡尔·门格在1926年描述，当时他正在研究拓扑维数的概念。

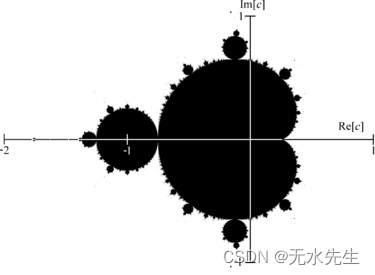
3.3  曼德博集合

        是基于复平面的分形典范。曼德博集合可以用复二次多项式来定义：

     ，其中c 是一个复数参数。

从z = 0开始迭代：

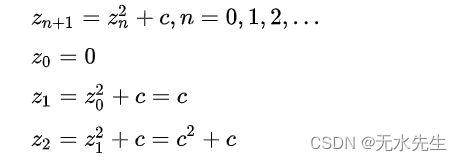
        不同的参数c可能使序列的绝对值逐渐发散到无限大，也可能收敛在有限的区域内。曼德博集合M 就是使序列不延伸至无限大的所有复数c的集合。

3.4 科赫雪花

        科赫雪花是由瑞典数学家科赫在 1904 年提出的一种不规则几何图形，也称为雪花曲线。

        分形图形的特点是整体几何图形是由一个微图形结构自我复制、反复叠加形成，且最终形成的整体图案和微图形结构一样。在编写分形算法时，需要先理解微图案的生成过程。

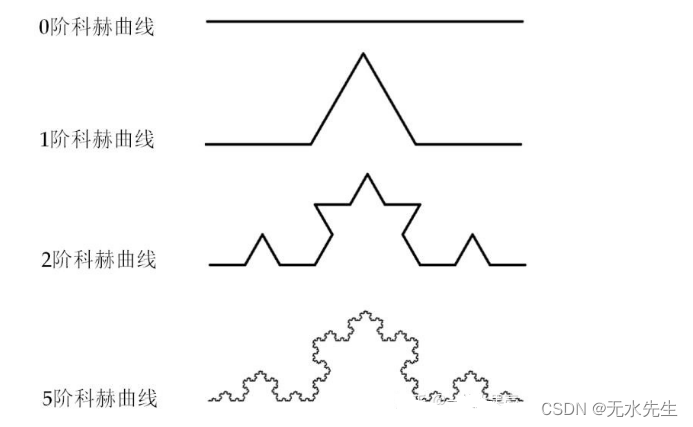
科赫雪花的微图案生成过程：

•  先画一条直线。科赫雪花本质就由一条直线演化而成。
• 三等分画好的直线。
• 取中间线段，然后用夹角为 60° 的两条等长线段替代。
• 可在每一条线段上都采用如上方式进行迭代操作，便会构造出多层次的科赫雪花。

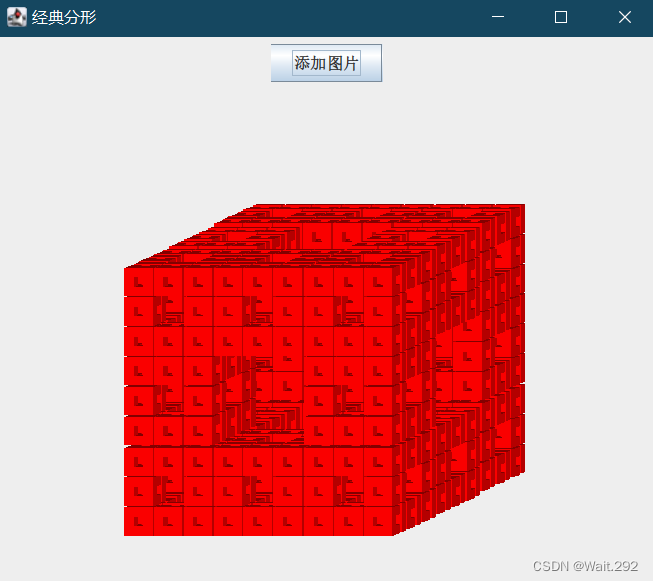
四、谢尔宾斯基地毯代码实现 

4.1 算法代码：

# importing necessary modules
import numpy as np
from PIL import Image# total number of times the process will be repeated
total = 7# size of the image
size = 3 ** total# creating an image
square = np.empty([size, size, 3], dtype=np.uint8)
color = np.array([255, 255, 255], dtype=np.uint8)# filling it black
square.fill(0)for i in range(0, total + 1):stepdown = 3 ** (total - i)for x in range(0, 3 ** i):# checking for the centremost squareif x % 3 == 1:for y in range(0, 3 ** i):if y % 3 == 1:# changing its colorsquare[y * stepdown:(y + 1) * stepdown, x * stepdown:(x + 1) * stepdown] = color# saving the image produced
save_file = "sierpinski.jpg"
Image.fromarray(square).save(save_file)# displaying it in console
i = Image.open("sierpinski.jpg")
i.show()

4.2 谢尔宾斯基地毯结果：

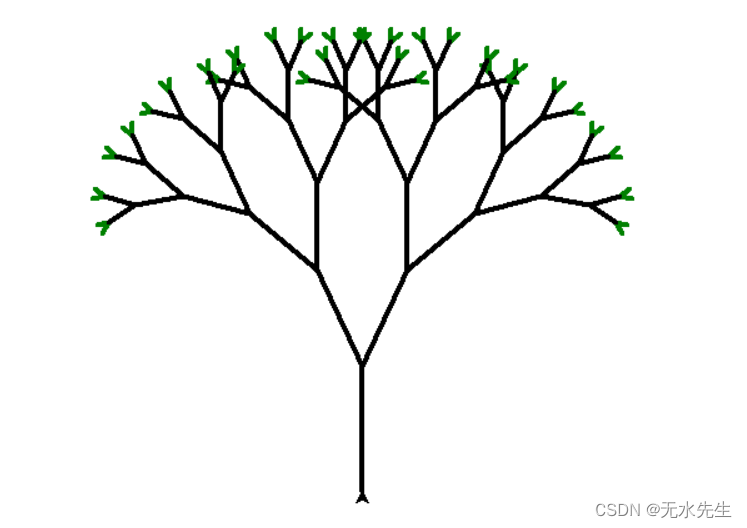
五、分形树代码实现

5.1 分形树代码

import turtledef draw_tree(length):if length>=5:#设定颜色if length <=15:turtle.color('green')else:turtle.color('black')'''先画右侧树枝'''#向前turtle.forward(length)#右转25度turtle.right(25)#递归draw_treedraw_tree(length - 15)'''画左侧树枝'''#左转50度turtle.left(50)#递归draw_treedraw_tree(length - 15)'''回退'''#设定颜色if length <=15:turtle.color('green')else:turtle.color('black')#右转25度turtle.right(25)#回退turtle.backward(length)def main():#起始点往下移100turtle.pensize(4)turtle.left(90)turtle.penup()turtle.backward(100)turtle.pendown()draw_tree(100)turtle.exitonclick()if __name__ == '__main__':main()

5.2 分形树结果 

六、曼德博集合代码

6.1 代码

from PIL import Image
import colorsys
import math
import os#frame parameters
width = 1000 #pixels
x = -0.65
y = 0
xRange = 3.4
aspectRatio = 4/3precision = 500height = round(width / aspectRatio)
yRange = xRange / aspectRatio
minX = x - xRange / 2
maxX = x + xRange / 2
minY = y - yRange / 2
maxY = y + yRange / 2img = Image.new('RGB', (width, height), color = 'black')
pixels = img.load()def logColor(distance, base, const, scale):color = -1 * math.log(distance, base)rgb = colorsys.hsv_to_rgb(const + scale * color,0.8,0.9)return tuple(round(i * 255) for i in rgb)def powerColor(distance, exp, const, scale):color = distance**exprgb = colorsys.hsv_to_rgb(const + scale * color,1 - 0.6 * color,0.9)return tuple(round(i * 255) for i in rgb)for row in range(height):for col in range(width):x = minX + col * xRange / widthy = maxY - row * yRange / heightoldX = xoldY = yfor i in range(precision + 1):a = x*x - y*y #real component of z^2b = 2 * x * y #imaginary component of z^2x = a + oldX #real component of new zy = b + oldY #imaginary component of new zif x*x + y*y > 4:breakif i < precision:distance = (i + 1) / (precision + 1)rgb = powerColor(distance, 0.2, 0.27, 1.0)pixels[col,row] = rgbindex = row * width + col + 1print("{} / {}, {}%".format(index, width * height, round(index / width / height * 100 * 10) / 10))img.save('output.png')
os.system('open output.png')

6.2 运算结果 

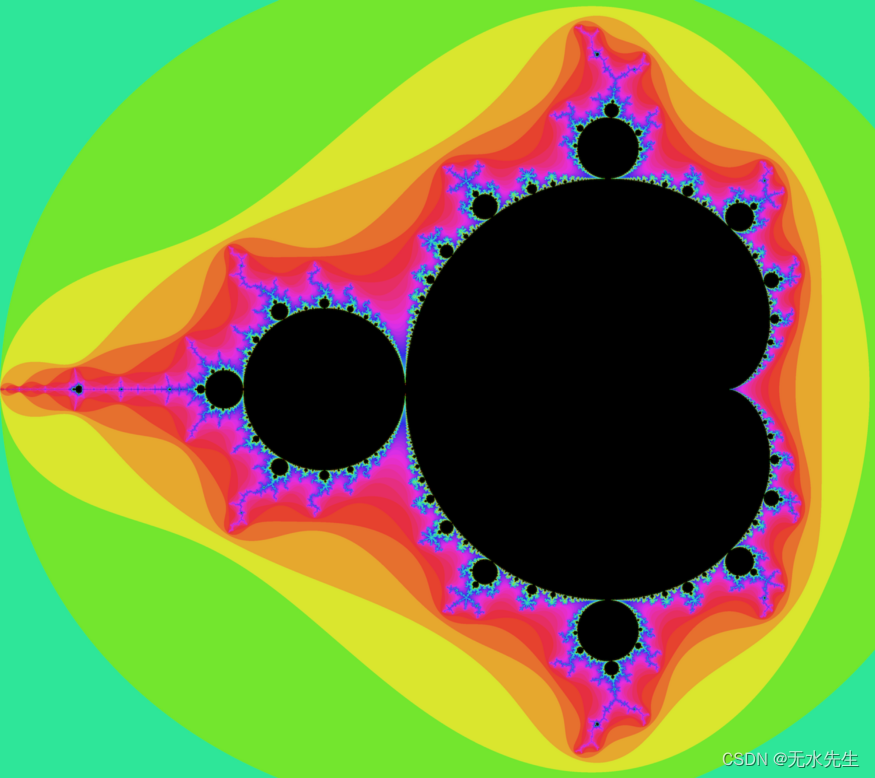
七  科赫雪花代码

7.1 科赫雪花代码

import turtle
turtle.speed(100)
def ke_line(line_, n):if n == 0:turtle.fd(line_)else:line_len = line_ // 3for i in [0, 60, -120, 60]:turtle.left(i)ke_line(line_len, n - 1)
# 原始线长度
line = 300
# 移动小海龟画布左下角
turtle.penup()
turtle.goto(-150, -150)
turtle.pendown()
# 几阶科赫雪花
di_gui_deep = int(input("请输入科赫雪花的阶数："))
while True:# 当多少科赫雪花围绕成一个圆周时，就构成一个完整的雪花造型count = int(input("需要几个科赫雪花："))if 360 % count != 0:print("请输入 360 的倍数")else:break
for i in range(count):ke_line(line, di_gui_deep)turtle.left(360 // count)
turtle.done()

7.2 结果

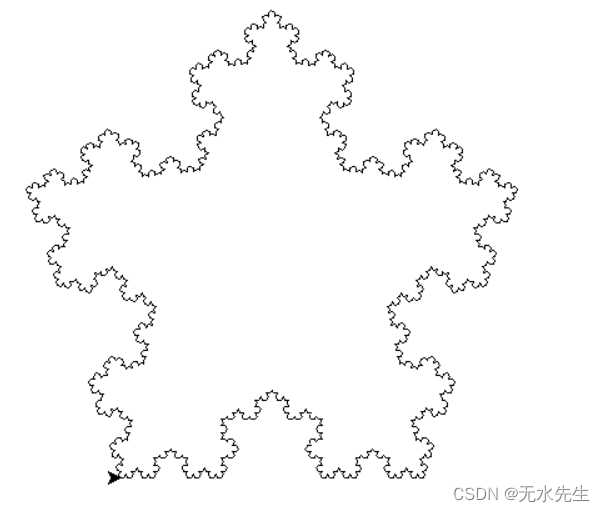
八、后记

        有专门的理论教学《分形几何》，其中的内容更加丰富， 我们将在以后的博客中继续介绍。